江苏省苏州市2022-2023学年高一下学期期末迎考数学试题
试卷更新日期:2023-08-18 类型:期末考试
一、单选题
-
1. 已知复数 , 若 , 则的虚部是( )A、 B、 C、2 D、2. 从某班名同学中选出人参加户外活动,利用随机数表法抽取样本时,先将名同学按、、、进行编号,然后从随机数表第行的第列和第列数字开始往右依次选取两个数字,则选出的第个同学的编号为( )
0347
4373
8636
9647
3661
4698
6371
6297
7424
6292
4281
1457
2042
5332
3732
1676
(注:表中的数据为随机数表第行和第行)
A、 B、 C、 D、3. 设 , 是两条不同的直线, , 是两个不同的平面,则下列结论不正确的是( )A、若 , , 则 B、若 , , 则 C、若 , , 则 D、若 , , , , 与相交,则4. 一组数据按从小到大的顺序排列为2,3,4, , 7,8(其中),若该组数据的中位数是极差的 , 则该组数据的60%分位数是( )A、4 B、4.5 C、5 D、65. 已知 , 则( )A、 B、 C、 D、6. 已知事件 , , 且 , , 如果与互斥,那么 , 如果与相互独立,那么 , 则 , 分别为( )A、 , B、 , C、 , D、 ,7. 如图,在中,点 , 分别在边和边上, , 分别为和的三等分点,点靠近点 , 点靠近点 , 交于点 , 设 , , 则( )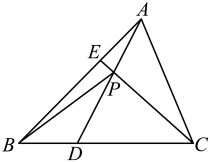 A、 B、 C、 D、8. 蹴鞠,又名蹴球,踢圆等,蹴有用脚蹴、踢、蹋的含义,鞠最早系外包皮革、内实米糠的球.因而蹴鞠就是指古人以脚蹴、蹋、踢皮球的活动,类似今日的足球.2006年5月20日,蹴鞠已作为非物质文化遗产经国务院批准列入第一批国家非物质文化遗产名录.已知某鞠的表面上有四个点 , , , 恰好构成三棱锥 , 若 , , 且 , , , , 则该鞠的表面积为( )A、 B、 C、 D、
A、 B、 C、 D、8. 蹴鞠,又名蹴球,踢圆等,蹴有用脚蹴、踢、蹋的含义,鞠最早系外包皮革、内实米糠的球.因而蹴鞠就是指古人以脚蹴、蹋、踢皮球的活动,类似今日的足球.2006年5月20日,蹴鞠已作为非物质文化遗产经国务院批准列入第一批国家非物质文化遗产名录.已知某鞠的表面上有四个点 , , , 恰好构成三棱锥 , 若 , , 且 , , , , 则该鞠的表面积为( )A、 B、 C、 D、二、多选题
-
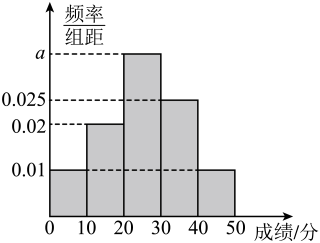
9. 已知向量 , , 下列结论中正确的是( )A、若 , 则 B、若 , 则 C、当时,与的夹角为锐角 D、若 , 则与的夹角的余弦值为10. 为了进一步培养全校学生的法律意识,强化学生自我保护能力,知法守法,某中学举行法规知识竞赛(满分分),对全校参赛的名学生的得分情况进行了统计,把得分数据按照、、、、分成组,绘制了如图所示的频率分布直方图,根据图中信息,下列说法正确的是( )
 A、 B、得分在区间内的学生人数为 C、该校学生法规竞赛成绩的中位数大于 D、估计该校学生法规竞赛成绩的平均数落在区间内11. 在中, , , 分别为角 , , 的对边,下列叙述正确的是( )A、若 , 则为等腰三角形 B、已知 , , 则 C、若 , 则 D、若 , 则为锐角三角形12. 如图,在正方体中,点在线段上运动,下列判断中正确的是( )
A、 B、得分在区间内的学生人数为 C、该校学生法规竞赛成绩的中位数大于 D、估计该校学生法规竞赛成绩的平均数落在区间内11. 在中, , , 分别为角 , , 的对边,下列叙述正确的是( )A、若 , 则为等腰三角形 B、已知 , , 则 C、若 , 则 D、若 , 则为锐角三角形12. 如图,在正方体中,点在线段上运动,下列判断中正确的是( )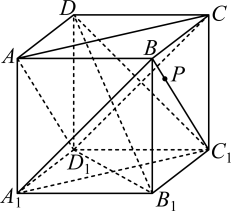 A、平面平面 B、 C、 D、异面直线与所成角的取值范围是
A、平面平面 B、 C、 D、异面直线与所成角的取值范围是三、填空题
-
13. 从 , , , , 这五个数中任选两个不同的数,则这两个数的和小于的概率为.14. 如图,长方体的底面的斜二测直观图为平行四边形.已知 , , 高 , , 分别为 , 的中点,用平面截该长方体,则剩余的三棱台的体积为.
 15. 自古以来,人们对于崇山峻岭都心存敬畏,同时感慨大自然的鬼斧神工,一代诗圣杜甫曾赋诗《望岳》:“贷宗夫如何?齐鲁青未了.造化钟神秀,阴阳割昏晓,.荡胸生层云,决眦入归鸟.会当凌绝顶,一览众山小.”然而,随着技术手段的发展,山高路远便 不再是人们出行的阻碍,伟大领袖毛主席曾作词:“一桥飞架南北,天堑变通途”.在科技腾飞的当下,路桥建设部门仍然潜心研究如何缩短空间距离方便出行,如港珠澳跨海大桥等.如图,某工程队将从到修建一条隧道,工程队从出发向正东行到达 , 然后从向南偏西方向行了一段距离到达 , 再从向北偏西方向行了到达 , 已知在南偏东方向上,则到修建隧道的距离为.
15. 自古以来,人们对于崇山峻岭都心存敬畏,同时感慨大自然的鬼斧神工,一代诗圣杜甫曾赋诗《望岳》:“贷宗夫如何?齐鲁青未了.造化钟神秀,阴阳割昏晓,.荡胸生层云,决眦入归鸟.会当凌绝顶,一览众山小.”然而,随着技术手段的发展,山高路远便 不再是人们出行的阻碍,伟大领袖毛主席曾作词:“一桥飞架南北,天堑变通途”.在科技腾飞的当下,路桥建设部门仍然潜心研究如何缩短空间距离方便出行,如港珠澳跨海大桥等.如图,某工程队将从到修建一条隧道,工程队从出发向正东行到达 , 然后从向南偏西方向行了一段距离到达 , 再从向北偏西方向行了到达 , 已知在南偏东方向上,则到修建隧道的距离为. 16. 已知我国某省二、三、四线城市数量之比为 . 年月份调查得知该省二、三、四线城市房产均价为万元/平方米,方差为 . 其中三、四线城市的房产均价分别为万元/平方米,万元/平方米,三、四线城市房价的方差分别为 , 则二线城市房产均价为万元/平方米,二线城市房价的方差为
16. 已知我国某省二、三、四线城市数量之比为 . 年月份调查得知该省二、三、四线城市房产均价为万元/平方米,方差为 . 其中三、四线城市的房产均价分别为万元/平方米,万元/平方米,三、四线城市房价的方差分别为 , 则二线城市房产均价为万元/平方米,二线城市房价的方差为四、解答题
-
17. 已知复数为纯虚数.(1)、求的值;(2)、若 , 求.18. 已知甲的投篮命中率为0.6,乙的投篮命中率为0.7,丙的投篮命中率为0.5.(1)、甲、乙、丙各投篮一次,求甲和乙命中,丙不命中的概率;(2)、甲、乙、丙各投篮一次,求恰有一人命中的概率;(3)、甲、乙、丙各投篮一次,求至少有一人命中的概率.19. 在钝角三角形中, , , , .(1)、求的值;(2)、已知 , , 三点共线,若恒成立,求实数的取值范围.

