湖北省十堰市2022-2023学年高二下学期6月期末数学试题

试卷更新日期：2023-08-18 类型：期末考试

进入出卷网下载

一、单选题

1. 在等比数列 ${a_{n}}$ 中， $a_{4} = 4 ， a_{6} = 1$ ，则 $a_{5} =$ （）

A、1 B、2 C、 $\pm 1$ D、 $\pm 2$

查看试题解析
2. 函数 $f (x) = \frac{\cos x}{x}$ 的导数 $f^{'} (x) =$ （）

A、 $\frac{x \sin x - \cos x}{x^{2}}$ B、 $\frac{- x \sin x - \cos x}{x^{2}}$ C、 $\frac{x \sin x + \cos x}{x^{2}}$ D、 $\frac{- x \sin x + \cos x}{x^{2}}$

查看试题解析
3. 若随机变量 $X ∼ B (10 ， 0.6)$ ，则 $D (2 X - 1) =$ （）

A、4.8 B、2.4 C、9.6 D、8.6

查看试题解析
4. 已知 $(2 x - 1)^{2024} = a_{0} + a_{1} x + a_{2} x^{2} + ⋯ + a_{2024} x^{2024}$ ，则 $a_{1} + a_{2} + a_{3} + ⋯ + a_{2024} =$ （）

A、1 B、0 C、 $3^{2024}$ D、 $- 1$

查看试题解析
5. 记 $a ， b ， c ， d$ 为 $1 ， 2 ， 3 ， 4$ 的任意一种排列，则使得 $(a + b) (c + d)$ 为偶数的排列种数为（）

A、8 B、12 C、16 D、18

查看试题解析
6. $(1 - \frac{y}{x}) (2 x + y)^{8}$ 的展开式中 $x^{3} y^{5}$ 的系数为（）

A、 $- 672$ B、 $- 112$ C、672 D、112

查看试题解析
7. 若存在直线 $y = k x + b$ ，使得函数 $F (x)$ 和 $G (x)$ 对其公共定义域上的任意实数 $x$ 都满足 $F (x) \geq k x + b \geq G (x)$ ，则称此直线 $y = k x + b$ 为 $F (x)$ 和 $G (x)$ 的“隔离直线”.已知函数 $f (x) = x^{2}$ ， $g (x) = a l n x (a > 0)$ ，若 $f (x)$ 和 $g (x)$ 存在唯一的“隔离直线”，则 $a =$ （）

A、 $\sqrt{e}$ B、 $2 \sqrt{e}$ C、 $e$ D、 $2 e$

查看试题解析
8. 已知有编号为 $1 ， 2 ， 3$ 的三个盒子，其中1号盒子内装有两个1号球，一个2号球和一个3号球；2号盒子内装有两个1号球，一个3号球；3号盒子内装有三个2号球，两个3号球.若第一次先从1号盒子内随机抽取一个球，将取出的球放入与球同编号的盒子中，第二次从该盒子中任取一个球，则在两次取球编号不同的条件下（）

A、第二次取到1号球的概率最大 B、第二次取到2号球的概率最大 C、第二次取到3号球的概率最大 D、第二次取到 $1 ， 2 ， 3$ 号球的概率都相同

查看试题解析

二、多选题

9. 设数列 ${a_{n}}$ 、 ${b_{n}}$ 都是等比数列，则下列数列一定是等比数列的是（）

A、 ${a_{n} + b_{n}}$ B、 ${a_{n} b_{n}}$ C、 ${m a_{n}} (m \in R)$ D、 ${\frac{a_{n}}{b_{n}}}$

查看试题解析
10. 某同学求得一个离散型随机变量 $X$ 的分布列为

x

1

2

4

6

P

0.2

0.3

m

0.1

则（）

A、 $m = 0.4$ B、 $E (X) = 3$ C、 $D (X) = 1.4$ D、 $σ (X) = \frac{2 \sqrt{15}}{5}$

查看试题解析

11. 为研究如何合理施用有机肥，使其最大限度地促进某种作物的增产，同时减少对周围环境的污染，某研究团队收集了7组某种有机肥的施用量和当季该种作物的亩产量的数据，并对这些数据进行了初步处理，得到如表所示的一些统计量的值，其中，有机肥施用量为

x

（单位：千克），当季该种作物的亩产量为

y

（单位：百千克）.

$x$	1	2	4	6	11	13	19
$y$	1.9	3.2	4.0	4.4	5.2	5.3	5.4

现有两种模型可供选用，模型I为线性回归模型，利用最小二乘法，可得到 $y$ 关于 $x$ 的经验回归方程为 $\hat{y} = 0.17 x + \hat{a}$ ，模型II为非线性经验回归方程 $\hat{y} = c + d \sqrt{x}$ ，经计算可得此方程为 $\hat{y} = 1.63 + 0.99 \sqrt{x}$ ，另外计算得到模型I的决定系数 $R^{2} \approx 0.75$ 和模型II的决定系数 $R^{2} \approx 0.88$ ，则（）

A、

\hat{a} = 2.84

B、模型II的拟合效果比较好 C、在经验回归方程

\hat{y} = 0.17 x + \hat{a}

中，当解释变量

x

每增加1个单位时，响应变量

\hat{y}

一定增加0.17个单位 D、若7组数据对应七个点，则至少有一个点在经验回归直线上

查看试题解析

12. 已知定义域为 $R$ 的函数 $f (x)$ 的导函数为 $f^{'} (x)$ ，且 $f^{'} (x) > f (x)$ ，则下列不等式恒成立的是（）

A、 $e f (l n 2) > 2 f (1)$ B、 $e^{\sqrt{1.2}} f (e^{0.1}) > e^{e^{0.1}} f (\sqrt{1.2})$ C、 $\sqrt{2} f (\frac{1}{e}) > e^{\frac{1}{e}} f (l n \sqrt{2})$ D、 $e^{\frac{\sqrt{e}}{2}} f (2 l n 2) < 4 f (\frac{\sqrt{e}}{2})$

查看试题解析

三、填空题

13. 已知函数 $f (x) = x^{3} - 3 x - 1$ 在区间 $[- 3 ， 2]$ 上的最大值为 $M$ ，最小值为 $N$ ，则 $M N =$ .

查看试题解析
14. 设等比数列 ${a_{n}}$ 的前 $n$ 项和为 $S_{n}$ ，若 $\frac{S_{8}}{S_{4}} = 6$ ，则 $\frac{S_{16}}{S_{4}} =$ .

查看试题解析
15. $(2 x + 11)^{10}$ 的展开式中系数最大的项是第项.

查看试题解析

四、双空题

16. 法国数学家蒙德尔布罗的文章《英国的海岸线有多长？》标志着几何概念从整数维到分数维的飞跃.他将具有分数维的图形称为“分形”，并建立了以这类图形为对象的数学分支——分形几何.分形几何不只是扮演着计算机艺术家的角色，事实表明它是描述和探索自然界大量存在的不规则现象的工具.下面我们用分形的方法来得到一系列图形，如图1，线段 $A B$ 的长度为3，在线段 $A B$ 上取两个点 $C ， D$ ，使得 $A C = D B = \frac{1}{3} A B$ ，以 $C D$ 为一边在线段 $A B$ 的上方作一个正三角形，然后去掉线段 $C D$ ，得到图2中的图形；对图2中的线段 $E C ， E D$ 做相同的操作，得到图3中的图形.依此类推，则第 $n (n \geq 2 ， n \in N^{*})$ 个图形中新出现的等边三角形的边长为；第 $n$ 个图形（图1为第一个图形）中的所有线段长的和为.

查看试题解析

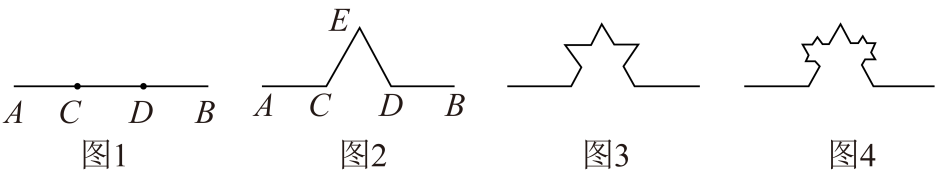
五、解答题

17. 已知等比数列 ${a_{n}}$ 的前 $n$ 项和为 $S_{n}$ ，且 $a_{n + 1} = 2 S_{n} + 1$ .

(1)、求 ${a_{n}}$ 的通项公式；

(2)、设 $b_{n} = n a_{n} (n \in N^{*})$ ，求数列 ${b_{n}}$ 的前 $n$ 项和 $T_{n}$ .

查看试题解析
18. 已知函数 $f (x) = a x^{3} - 3 x^{2} + 6 (a > 0)$ .

(1)、若 $x = 1$ 是 $f (x)$ 的极值点，求 $a$ ；

(2)、当 $a > 2$ 时， $f (x) > 0$ 在区间 $[- 1 ， 1]$ 上恒成立，求 $a$ 的取值范围.

查看试题解析
19. 世界卫生组织建议成人每周进行2.5至5小时的中等强度运动.已知 $A$ 社区有 $20 %$ 的居民每周运动总时间超过5小时， $B$ 社区有 $30 %$ 的居民每周运动总时间超过5小时， $C$ 社区有 $50 %$ 的居民每周运动总时间超过5小时，且 $A ， B ， C$ 三个社区的居民人数之比为 $3 ： 3 ： 4$ .

(1)、从这三个社区中随机各选取1名居民，求至少有1名居民每周运动总时间超过5小时的概率；

(2)、从这三个社区中随机抽取1名居民，求该居民每周运动总时间超过5小时的概率；

(3)、假设这三个社区每名居民每周运动总时间为随机变量 $X$ （单位：小时），且 $X ∼ N (4 ， σ^{2})$ ，现从这三个社区中随机选取1名居民，求该居民每周运动总时间为3至5小时的概率.

查看试题解析
20. 已知数列 ${a_{n}}$ 的前 $n$ 项和为 $S_{n} ， a_{1} = 1$ 且 $n S_{n + 1} = (n + 2) S_{n}$ .

(1)、求 ${a_{n}}$ 的通项公式；

(2)、 $b_{k}$ 为满足 $k \leq a_{n} \leq 2^{k}$ 的 $a_{n}$ 的个数，求使 $b_{1} + b_{2} + ⋯ + b_{k} > 2023$ 成立的最小正整数 $k$ 的值.

查看试题解析

21. 湖北省教育厅出台《全省学校安全专项治理工作方案》，加强校园“十防”、“七全”安全教育和防范工作.为了普及安全教育，增强学生安全意识，武汉市准备组织一次安全知识竞赛.某学校为了选拔学生参赛，按性别采用分层抽样的方法抽取200名学生进行安全知识测试，记

A =

“性别为男”，

B =

“得分超过85分”，且

P (A ∣ \bar{B}) = \frac{2}{5} ， P (B ∣ \bar{A}) = \frac{5}{8} ， P (B) = \frac{3}{4}

(1)、完成下列

2 \times 2

列联表，并根据小概率值

α = 0.001

的独立性检验，能否推断该校学生了解安全知识的程度与性别有关？

性别	了解安全知识的程度		合计
性别	得分不超过85分的人数	得分超过85分的人数	合计
男
女
合计

(2)、学校准备分别选取参与测试的男生和女生前两名学生代表学校参加竞赛，已知男生获奖的概率为

\frac{3}{4}

，女生获奖的概率为

\frac{2}{3}

，记该校获奖的人数为

X

，求

X

的分布列与数学期望.

附参考公式： $P (\bar{A} ∣ \bar{B}) = 1 - P (A ∣ \bar{B}) ， P (\bar{A} ∣ \bar{B}) \cdot P (\bar{B}) = P (\bar{B} ∣ \bar{A}) \cdot P (\bar{A})$ . $χ^{2} = \frac{n (a d - b c)^{2}}{(a + b) (c + d) (a + c) (b + d)}$ ，其中 $n = a + b + c + d$ .下表是 $χ^{2}$ 独立性检验中几个常用的小概率值和相应的临界值.

$α$	0.1	0.05	0.01	0.005	0.001
$x_{α}$	2.706	3.841	6.635	7.879	10.828

查看试题解析

22. 已知函数 $f (x) = x + \frac{a}{e^{x}} (a \in R)$ .

(1)、讨论 $f (x)$ 的单调性；

(2)、若 $f (x)$ 与函数 $g (x) = a e^{x}$ 的图象有三个不同的交点，求 $a$ 的取值范围.（参考数据： $l n 2 \approx 0.7$ .）

查看试题解析

x	1	2	4	6
P	0.2	0.3	m	0.1