河北省“五个一”名校联盟2022-2023学年高一下学期期末联考数学试题
试卷更新日期:2023-08-18 类型:期末考试
一、单选题
-
1. 已知向量 , 则下列选项中与共线的单位向量是( )A、; B、 C、 D、2. 某学校为了解学生参加体育运动的情况,用比例分配的分层随机抽样作抽样调查,拟从初中部和高中部两层共抽取名学生,已知该校初中部和高中部分别有和名学生,则正确的( )A、高中部产生个样本 B、初中部产生个样本 C、不同级部每个学生被抽取的可能性不相同 D、可以从两个级部各抽取个样本3. 已知为虚数单位,若复数 , 则下列四个选项正确的是( )A、 B、若是复数的共轭复数,则 C、复数的虚部为 D、复数在复平面内对应的点位于第一象限4. 若 的周长等于20,面积是 ,则 边的长是( )A、5 B、6 C、7 D、85. 已知平面向量满足 , , , 则向量与向量的夹角为( )A、 B、 C、 D、6. 元宵节是春节之后的第一个重要节日,元宵节又称灯节,很多地区家家户户都挂花灯.下图是小明为自家设计的一个花灯,该花灯由上面的正六棱台与下面的正六棱柱组成,若正六棱台的上、下两个底面的边长分别为40cm和20cm,正六棱台与正六棱柱的高分别为10cm和60cm,则该花灯的体积为( )
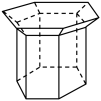 A、 B、 C、 D、7. 已知圆锥的顶点为 , 底面圆心为 , 为底面直径, , , 点在底面圆周上,且二面角为 , 则下列各选项正确的是( )A、该圆锥的体积为 B、该圆锥的侧面积为 C、 D、过圆锥任意两条母线的截面中面积最大的为8. 已知 , , 且 , 令 , 则( )A、 B、 C、 D、
A、 B、 C、 D、7. 已知圆锥的顶点为 , 底面圆心为 , 为底面直径, , , 点在底面圆周上,且二面角为 , 则下列各选项正确的是( )A、该圆锥的体积为 B、该圆锥的侧面积为 C、 D、过圆锥任意两条母线的截面中面积最大的为8. 已知 , , 且 , 令 , 则( )A、 B、 C、 D、二、多选题
-
9. 设为复数,则下列命题中一定成立的是( )A、如果 , 那么 B、如果 , 那么 C、如果 , 那么 D、如果 , 那么10. 小明在一次面试活动中,10位评委给他的打分分别为:70、85、86、88、90、90、92、94、95、100.则下列说法正确的有( )A、这10个分数的中位数为90 B、这10个分数的第60百分位数为91 C、这10个分数的平均数大于中位数 D、去掉一个最低分和一个最高分后,平均分数会变大,而分数的方差会变小11. 已知 , 函数 , 下列选项正确的有( )A、若的最小正周期 , 则 B、当时,函数的图象向右平移个单位长度后得到的图象 C、若在区间上单调递增,则的取值范围是 D、若在区间上只有一个零点,则的取值范围是12. 素描是使用单一色彩表现明暗变化的一种绘画方法,素描水平反映了绘画者的空间造型能力.“十字贯穿体”是学习素描时常用的几何体实物模型,如图是某同学绘制“十字贯穿体”的素描作品.“十字贯穿体”是由两个完全相同的正四棱柱“垂直贯穿”构成的多面体,其中一个四棱柱的每一条侧棱分别垂直于另一个四棱柱的每一条侧棱,两个四棱柱分别有两条相对的侧棱交于两点,另外两条相对的侧棱交于一点(该点为所在棱的中点).若该同学绘制的“十字贯穿体”由两个底面边长为2,高为6的正四棱柱构成,则( )
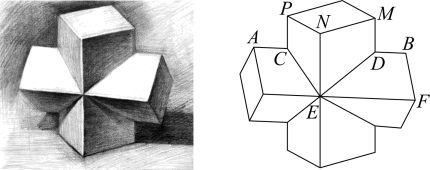 A、一个正四棱柱的某个侧面与另一个正四棱柱的两个侧面的交线互相垂直 B、该“十字贯穿体”的表面积是 C、该“十字贯穿体”的体积是 D、与所成角的余弦值是
A、一个正四棱柱的某个侧面与另一个正四棱柱的两个侧面的交线互相垂直 B、该“十字贯穿体”的表面积是 C、该“十字贯穿体”的体积是 D、与所成角的余弦值是三、填空题
-
13. 已知向量 , , 若 , 则 .14. 若复数满足(为实数),则的最大值为 .15. 已知四棱锥的底面是边长为2的正方形,底面 , , 则四棱锥外接球表面积为;若点是线段上的动点,则的最小值为 .16. 已知三角形的内角的对边分别是 , 若 , 为锐角,则的最小值为 .
四、解答题
-
17. 已知复数 , , 其中是虚数单位, .(1)、若为纯虚数,求的值;(2)、若 , 求的取值范围.18. 为了调查疫情期间物理网课学习情况,某校组织了高一年级学生进行了物理测试.根据测试成绩(总分100分),将所得数据按照 , , , , , 分成6组,其频率分布直方图如图所示.
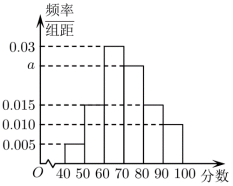 (1)、求图中a的值;(2)、试估计本次物理测试成绩的平均分;(同一组中的数据用该组区间的中点值作代表)(3)、该校准备对本次物理测试成绩优异(将成绩从高到低排列,排在前13%的为优异)的学生进行嘉奖,则受嘉奖的学生分数不低于多少?19. 如图是函数的部分图象,已知 .
(1)、求图中a的值;(2)、试估计本次物理测试成绩的平均分;(同一组中的数据用该组区间的中点值作代表)(3)、该校准备对本次物理测试成绩优异(将成绩从高到低排列,排在前13%的为优异)的学生进行嘉奖,则受嘉奖的学生分数不低于多少?19. 如图是函数的部分图象,已知 .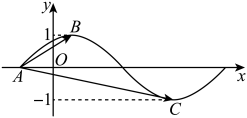 (1)、求;(2)、若 , 求 .
(1)、求;(2)、若 , 求 .