湖南省名校联考联合体2022-2023学年高二下学期6月期末数学试题
试卷更新日期:2023-08-18 类型:期末考试
一、单选题
-
1. 已知集合 , , 则( )A、 B、 C、 D、2. 已知复数 , 且 , 其中 , 为实数,则( )A、 , B、 , C、 , D、 ,3. 已知非零向量 , 满足 , , , 则( )A、 B、 C、 D、4. 已知长方体的底面是边长为2的正方形, , , 分别为 , 的中点,则三棱锥的体积为( )A、 B、4 C、 D、65. 某学校在高考模拟考试座位的排定过程中,有来自班的4名学生和来自班的4名学生,恰好排在五行八座(每个考室5行*8座人)中的第二行,则来自同一班级的4名学生互不相邻的概率为( )A、 B、 C、 D、6. 已知 , 且的最小正周期为2.若存在 , 使得对于任意 , 都有 , 则为( )A、 B、 C、 D、7. 已知函数 , , 若 , , , 则 , , 的大小关系为( )A、 B、 C、 D、8. 已知 , , , 是表面积为的球面上四点, , , , 三棱锥的体积为 , 则线段长度的取值范围为( )A、 B、 C、 D、
二、多选题
-
9. 已知函数 , 则下列结论中正确的是( )A、可能是奇函数 B、在区间上单调递减 C、当的极大值为17时, D、当时,函数的值域是10. 已知抛物线:的焦点到准线的距离为2,则( )A、抛物线为 B、若 , 为上的动点,则的最小值为4 C、直线与抛物线相交所得弦长最短为4 D、若抛物线准线与轴交于点 , 点是抛物线上不同于其顶点的任意一点, , , 则的最小值为11. 已知正方体的棱长为2,则以下结论正确的是( )A、若为线段上动点(包括端点),则点到平面的距离为定值 B、正方形底面内存在点 , 使得 C、若点在正方体的表面上运动,点是的中点,点满足 , 则点的轨迹的周长为 D、当点为中点时,三棱锥的外接球半径12. 已知定义在的函数存在使为函数的最小值,其中 , 则的值可以为(附: , , )( )A、0 B、1 C、2 D、3
三、填空题
-
13. 在的展开式中常数项等于.14. 若一直线与曲线和曲线相切于同一点 , 则的值为.15. 有穷等差数列的各项均为正数,若 , 则的最小值是.16. 如图,已知双曲线:与过其焦点的圆相交于 , , , 四个点,直线与轴交于点 , 直线与双曲线交于点 , 记直线 , 的斜率分别为 , , 若 , 则双曲线的离心率为.
四、解答题
-
17. 在数列中, , .(1)、证明是等比数列;(2)、若 , 求数列的前项和.18. 已知函数在一个周期内一系列对应的值如下表:
…
…
…
0
2
0
…
(1)、求的解析式;(2)、若在锐角中, , 角所对的边 , 求面积的取值范围.19. 一个小型制冰厂有3台同一型号的制冰设备,在一天内这3台设备只要有一台能正常工作,制冰厂就会有利润,当3台都无法正常工作时制冰厂就因停业而亏本(3台设备相互独立,3台都正常工作时利润最大).每台制冰设备的核心系统由3个同一型号的电子元件组成,3个元件能正常工作的概率都为 , 它们之间相互不影响,当系统中有不少于的电子元件正常工作时,此台制冰设备才能正常工作.(1)、当时,求一天内制冰厂不亏本的概率;(2)、若已知当前每台设备能正常工作的概率为0.6,根据以往经验可知,若制冰厂由于设备不能正常工作而停业一天,制冰厂将损失1万元,为减少经济损失,有以下两种方案可供选择参考:方案1:更换3台设备的部分零件,使每台设备能正常工作的概率为0.85,更新费用共为600元.
方案2:对设备进行维护,使每台设备能正常工作的概率为0.75,设备维护总费用为元.请从期望损失最小的角度判断如何决策?
20. 如图,圆柱的轴截面是边长 , 的矩形,点在上底面圆内,且( , , 三点不在一条直线上).下底面圆的一条弦交于点 , 其中 , 平面平面.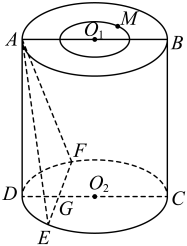 (1)、证明:平面;(2)、若二面角的正切值为 , 求的长.
(1)、证明:平面;(2)、若二面角的正切值为 , 求的长.