江苏省南京市江宁区2022-2023学年高二下学期期末数学试题
试卷更新日期:2023-08-18 类型:期末考试
一、单选题
-
1. 已知集合 , , 则( )A、 B、 C、 D、2. 已知(i为虚数单位),则复数的模为( )A、1 B、 C、2 D、33. 已知 , 是平面中两个不共线的向量,若 , , 且 , 则( )A、 B、 C、 D、4. 各项均为正数的等比数列 , 公比为 , 则“”是“为递增数列”的( )A、充分且不必要条件 B、必要且不充分条件 C、充要条件 D、既不充分又不必要条件5. 已知函数在区间上单调递增,则的取值范围是( )A、 B、 C、 D、6. 五张卡片上分别写有、、、、五个数字,则这五张卡片组成的五位数是偶数的概率( )A、 B、 C、 D、7. 故宫太和殿是中国形制最高的宫殿,其建筑采用了重檐庑殿顶的屋顶样式,庑殿顶是“四出水”的五脊四坡式,由一条正脊和四条垂脊组成,因此又称五脊殿.由于屋顶有四面斜坡,故又称四阿顶.如图,某几何体有五个面,其形状与四阿顶相类似.已知底面为矩形,∥底面 , , 与是全等的等边三角形,则该五面体的体积为( )
 A、 B、 C、 D、8. 直线过圆的圆心,且与圆相交于 , 两点,为双曲线右支上一个动点,则的最小值为( )A、0 B、1 C、2 D、3
A、 B、 C、 D、8. 直线过圆的圆心,且与圆相交于 , 两点,为双曲线右支上一个动点,则的最小值为( )A、0 B、1 C、2 D、3二、多选题
-
9. 某班名学生参加数学竞赛,将所有成绩分成、、、、五组,成绩的频率分布直方图如图所示,则下列说法正确的是( )
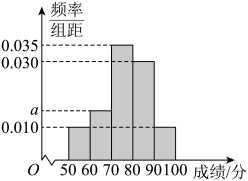 A、的值为 B、这名同学成绩的平均数在与之间 C、这名同学成绩的众数是 D、估计这名同学成绩的百分位数为10. 下列说法正确的是( )A、已知命题:任意 , , 则命题的否定为:存在 , B、若关于的不等式的解集为 , 则 C、如果 , , , 那么的最小值为6 D、函数的最小值为211. 设函数的最小正周期为 , 且过点 , 则下列说法正确的是( )A、为偶函数 B、的一条对称轴为 C、把的图象向左平移个单位长度后得到函数 , 则 D、若在上单调递减,则的取值范围为12. 已知是抛物线的焦点, , 是抛物线上的两点,为坐标原点,则( )A、抛物线的准线方程为 B、若 , 则的面积为 C、若直线过焦点 , 且 , 则到直线的距离为 D、若 , 则
A、的值为 B、这名同学成绩的平均数在与之间 C、这名同学成绩的众数是 D、估计这名同学成绩的百分位数为10. 下列说法正确的是( )A、已知命题:任意 , , 则命题的否定为:存在 , B、若关于的不等式的解集为 , 则 C、如果 , , , 那么的最小值为6 D、函数的最小值为211. 设函数的最小正周期为 , 且过点 , 则下列说法正确的是( )A、为偶函数 B、的一条对称轴为 C、把的图象向左平移个单位长度后得到函数 , 则 D、若在上单调递减,则的取值范围为12. 已知是抛物线的焦点, , 是抛物线上的两点,为坐标原点,则( )A、抛物线的准线方程为 B、若 , 则的面积为 C、若直线过焦点 , 且 , 则到直线的距离为 D、若 , 则三、填空题
-
13. 已知 , 则 .14. 展开式中,的系数为 . (以数字形式作答).15. 曲线在点处的切线方程为.16. 在三棱锥中,面 , 为等边三角形,且 , 则三棱锥的外接球的表面积为 .
四、解答题
-
17. 袋子中有6个大小相同的小球,其中4个白球、2个黑球.(1)、每次从袋子中随机摸出1个球,摸完不放回,共摸2次,求第二次摸到的球是白球的概率;(2)、一次完整的试验要求:从袋子中随机摸出1个球,记录小球的颜色后再把小球放回袋中.试验终止的条件是黑色小球出现两次,或者试验进行了4次.设试验终止时试验的次数为 , 求随机变量的数学期望.18. 中,角 , , 所对的边分别是 , , , 满足: ,(1)、求角;(2)、若 , 求的取值范围.19. 已知函数 .(1)、讨论的单调性;(2)、证明:当时, .
