安徽省滁州市2022-2023学年高一下学期教学质量监测数学试题

试卷更新日期：2023-08-18 类型：期末考试

进入出卷网下载

一、单选题

1. 已知集合 $A = {x | x^{2} - 2 x = 0}$ ， $B = {x | x \leq 3 ， x \in N}$ ，则 $A ∩ B =$ （）

A、 ${2}$ B、 ${0 ， 1 ， 2 ， 3}$ C、 ${1 ， 2}$ D、 ${0 ， 2}$

查看试题解析
2. 已知平面向量 $\vec{a} = (- 2 ， 0)$ ， $\vec{b} = (\frac{1}{2} ， - \frac{\sqrt{3}}{2})$ ，则 $| \frac{1}{2} \vec{a} - \vec{b} | =$ （）

A、1 B、2 C、 $\sqrt{3}$ D、3

查看试题解析
3. “ $b \neq 0$ ”是“复数 $a + b i$ ( $a ， b \in R$ )为纯虚数”的（）

A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件

查看试题解析
4. 一组数据为2，4，4，5，7，8，则这组数据的第60百分位数是（）

A、3 B、4 C、4.5 D、5

查看试题解析
5. 若 $c o s (x + \frac{π}{3}) = \frac{1}{3}$ ，则 $s i n (2 x + \frac{π}{6}) =$ （）

A、 $\frac{7}{9}$ B、 $- \frac{7}{9}$ C、 $\frac{2 \sqrt{2}}{3}$ D、 $- \frac{2 \sqrt{2}}{3}$

查看试题解析
6. 碳14是碳元素的一种同位素，具有放射性.活体生物其体内的碳14含量大致不变，当生物死亡后，其组织内的碳14开始衰变并逐渐消失.已知碳14的半衰期为5730年，即生物死亡t年后，碳14所剩质量 $C (t) = C_{0} {(\frac{1}{2})}^{\frac{t}{5730}}$ ，其中C₀为活体组织中碳14的质量.科学家一般利用碳14这一特性测定生物死亡年代.2023年科学家发现某生物遗体中碳14含量约为原始质量的0.8倍，依据计算结果并结合下图中我国历史朝代的时间轴可推断该生物死亡的朝代为（）(参考数据： $l g 2 \approx 0.3010$ )

A、西汉 B、东汉 C、三国 D、晋朝

查看试题解析
7. 如图，在平面四边形 $A B C D$ 中，E ， F分别为 $B D$ 和 $A C$ 的中点，那么（）

A、 $\vec{E F} = \frac{1}{2} \vec{A B} + \frac{1}{2} \vec{D C}$ B、 $\vec{E F} = \frac{1}{2} \vec{A B} - \frac{1}{2} \vec{D C}$ C、 $\vec{E F} = - \frac{1}{2} \vec{A B} + \frac{1}{2} \vec{D C}$ D、 $\vec{E F} = - \frac{1}{2} \vec{A B} - \frac{1}{2} \vec{D C}$

查看试题解析
8. 已知函数 $f (x) = m^{2} c o s x - m \cdot 2^{x + 1}$ 的图象和函数 $g (x) = \frac{m}{2^{x - 1}} - 3$ 的图象有唯一交点，则实数m的值为（）

A、1 B、3 C、 $- 1$ 或3 D、1或3

查看试题解析

二、多选题

9. 已知函数 $f (x) = s i n x - \sqrt{3} c o s x$ ，则（）

A、 $f (x)$ 的最小正周期为 $2 π$ B、 $f (x)$ 的图象关于直线 $x = \frac{π}{2}$ 对称 C、 $f (x)$ 的图象关于点 $(\frac{π}{3} ， 0)$ 对称 D、 $f (x)$ 在区间 $(\frac{π}{2} ， π)$ 上单调递减

查看试题解析
10. 抛掷一蓝、一黄两枚质地均匀的正方体骰子，设事件A为“两颗骰子点数之和大于7”，事件B为“黄骰子点数为偶数”，则（）

A、 $P (\bar{A}) = \frac{7}{12}$ B、事件A与B相互独立 C、 $P (A B) = \frac{1}{6}$ D、 $P (A \cup B) = \frac{2}{3}$

查看试题解析
11. 已知正数a ， b满足 $a + b = 1$ ，则（）

A、ab的最大值为 $\frac{1}{4}$ B、 $\frac{1}{a} + \frac{1}{b}$ 的最小值为4 C、 $\sqrt{a} + \sqrt{b}$ 的最小值为 $\sqrt{2}$ D、 $a - \frac{1}{b}$ 的最大值为 $- 1$

查看试题解析
12. 如图，圆锥PO的底面半径为2，高为4，点C是圆O上异于直径AB端点的动点，则（）

A、圆锥PO的侧面积为 $4 \sqrt{5} π$ B、四面体 $P - A B C$ 体积的最大值为 $\frac{16}{3}$ C、若 $∠ A B C = 60 °$ ，则二面角 $P - B C - A$ 的余弦值为 $\frac{4 \sqrt{19}}{19}$ D、若 $A B = \sqrt{2} B C$ ， E是母线PC上的动点，则 $A E + B E$ 的最小值为 $\frac{12 \sqrt{5}}{5}$

查看试题解析

三、填空题

13. 复数 $z$ 满足 $（ 1 - i ） z = 2 i ，则 | z | =$

查看试题解析
14. 已知点A ， B ， C ， D ， E ， F均匀分布在圆O上，从这6个点中任取三个点，则以这三个点为顶点的三角形是等腰三角形的概率为.

查看试题解析
15. 在棱长为2的正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中，点E是棱 $A A_{1}$ 的中点，过点E作垂直于直线 $B C_{1}$ 的截面，则该截面的面积为.

查看试题解析

四、双空题

16. 已知平面向量 $\vec{a}$ ， $\vec{b}$ 满足 $| \vec{a} | = 1$ ， $| \vec{b} | = \sqrt{3}$ ，记向量 $\vec{a} - \vec{b}$ 与 $\vec{b}$ 的夹角为θ.
⑴若 $\vec{a} \cdot \vec{b} = \frac{3}{2}$ ，则 $θ =$ ；

⑵ $c o s θ$ 的取值范围为.

查看试题解析

五、解答题

17. 已知平面向量 $\vec{e_{1}} = (- 1 ， 2)$ ， $\vec{e_{2}} = (3 ， 4)$ .

(1)、若 $\vec{e_{1}}$ 与 $\vec{e_{1}} + λ \vec{e_{2}}$ 垂直，求实数 $λ$ 的值；

(2)、求 $\vec{e_{1}}$ 在 $\vec{e_{2}}$ 上投影向量的坐标.

查看试题解析
18. 如图，在四棱锥 $E - A B C D$ 中，DA⊥平面ABE ， $D A / / B C$ ， $B C = 1$ ， $D A = 2$ ， F是DE的中点.

(1)、证明： $C F / /$ 平面ABE；

(2)、若 $B A = B E = 2$ ，直线DE与平面ABE所成角为 $4 5^{∘}$ ，求直线CF与直线DB所成角的余弦值.

查看试题解析
19. 4月23日是世界读书日，又称“世界图书日”.今年是安徽省开展全民阅读活动的第十年，某市组织学生参加“书香安徽·皖美阅读”活动.为了解该市义务教育阶段学生每周读书时间，按小学生和初中生进行分层，采用比例分配的分层随机抽样方法抽取了样本量为1000的样本进行调查，其中小学生600人，初中生400人，发现他们的每周读书时间都在200～500分钟之间，进行适当分组后(每组都是左闭右开的区间)，画出频率分布直方图如图所示.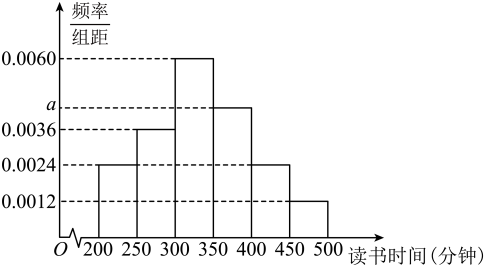

(1)、求a的值；

(2)、若上述样本中小学生每周读书时间的平均数为320分钟，请根据频率分布直方图估计样本中初中生每周读书时间的平均数.

查看试题解析
20. 在 $△ A B C$ 中，角A ， B ， C所对的边分别为a ， b ， c.已知 $a s i n A - b s i n B - c s i n C - b s i n C = 0$ .

(1)、求角A的大小；

(2)、若 $A B = 5$ ， $A C = 3$ ， AD是△ABC的角平分线，求AD的长.

查看试题解析
21. 已知定义在R上的偶函数 $f (x)$ 和奇函数 $g (x)$ 满足 $f (x) + g (x) = e^{x}$ .

(1)、 $f (x)$ 和 $g (x)$ ；

(2)、判断 $g (x)$ 的单调性，并用单调性的定义加以证明；

(3)、若不等式 $f (2 x) - m f (x) + 3 \geq 0$ 对一切实数x都成立，求实数m的取值范围.

查看试题解析
22. 如图，在四面体P-ABC中，△ABC是等腰三角形AB⊥BC ， $∠ P B A = ∠ P B C$ .

(1)、证明：PB⊥AC；

(2)、若AB=2， $P B = 2 \sqrt{5}$ ， PA⊥AB.
（ⅰ）求点A到平面PBC的距离；

（ⅱ）求二面角 $A - P C - B$ 的正弦值.

查看试题解析