广东湛江市2022-2023学年高二下学期期末数学试题

试卷更新日期：2023-08-18 类型：期末考试

进入出卷网下载

一、单选题

1. 设全集 $U = {0 ， 1 ， 2 ， 4 ， 6 ， 8}$ ，集合 $M = {0 ， 4 ， 6} ， N = {0 ， 1 ， 6}$ ，则 $M \cup ∁_{U} N =$ （）

A、 ${0 ， 2 ， 4 ， 6 ， 8}$ B、 ${0 ， 1 ， 4 ， 6 ， 8}$ C、 ${1 ， 2 ， 4 ， 6 ， 8}$ D、 $U$

查看试题解析
2. 已知 $a ， b \in R$ ， $i$ 是虚数单位，若 $a + 2 i$ 与 $1 + b i$ 互为共轭复数，则 $b =$ （）

A、 $1$ B、 $- 1$ C、 $2$ D、 $- 2$

查看试题解析
3. 已知 $θ$ 是第二象限角， $s i n (θ + \frac{π}{4}) = \frac{3}{5}$ ，则 $t a n θ =$ （）

A、 $- \frac{3}{4}$ B、 $- \frac{4}{3}$ C、 $- \frac{1}{7}$ D、 $- 7$

查看试题解析
4. 圆台的上､下底面半径分别是 $r = 1 ， R = 4$ ，且圆台的母线长为5，则该圆台的体积是（）

A、 $30 π$ B、 $28 π$ C、 $25 π$ D、 $24 π$

查看试题解析
5. 已知 $\vec{a} = (1 ， 2 ， - y)$ ， $\vec{b} = (x ， 1 ， 2)$ ，且 $(\vec{a} + 2 \vec{b}) / / (2 \vec{a} - \vec{b})$ ，则（）

A、 $x = \frac{1}{3}$ ， $y = 1$ B、 $x = \frac{1}{2}$ ， $y = - 4$ C、 $x = 2$ ， $y = - \frac{1}{4}$ D、 $x = 1$ ， $y = - 1$

查看试题解析
6. 有一组样本数据如下：
56，62，63，63，65，66，68，69，71，74，76，76，77，78，79，79，82，85，87，88，95，98
则其25%分位数、中位数与75%分位数分别为（）

A、65，76，82 B、66，74，82 C、66，76，79 D、66，76，82

查看试题解析
7. 已知 $x^{2} + y^{2} + 2 k x - 4 y + k^{2} + k - 2 = 0$ 表示的曲线是圆，则 $k$ 的值为（）

A、 $(6 ， + \infty)$ B、 $[- 6 ， + \infty)$ C、 $(- \infty ， 6)$ D、 $(- \infty ， 6]$

查看试题解析

二、多选题

8. （多选）对于抛物线上 $\frac{1}{8} x^{2} = y$ ，下列描述正确的是（）

A、开口向上，焦点为 $(0 ， 2)$ B、开口向上，焦点为 $(0 ， \frac{1}{16})$ C、焦点到准线的距离为4 D、准线方程为 $y = - 4$

查看试题解析
9. 下列命题是真命题的有（）

A、A ， B ， M ， N是空间四点，若 $\vec{B A} ， \vec{B M} ， \vec{B N}$ 不能构成空间的一个基底，那么A ， B ， M ， N共面 B、直线l的方向向量为 $\vec{a} = (\begin{array}{l} 1 ， - 1 ， 2 \end{array})$ ，直线m的方向向量为 $\vec{b} = (2 ， 1 ， - \frac{1}{2})$ ，则l与m垂直 C、直线l的方向向量为 $\vec{a} = (\begin{array}{l} 0 ， 1 ， - 1 \end{array})$ ，平面α的法向量为 $\vec{n} = (\begin{array}{l} 1 ， - 1 ， - 1 \end{array})$ ，则l⊥α D、平面α经过三点 $A (1 ， 0 ， - 1) ， B (0 ， 1 ， 0) ， C (- 1 ， 2 ， 0) ， \vec{n} = (1 ， u ， t)$ 是平面α的法向量，则 $u + t = 1$

查看试题解析
10. 有一散点图如图所示，在5个 $(x ， y)$ 数据中去掉 $D (3 ， 10)$ 后，下列说法中正确的是（）

A、残差平方和变小 B、相关系数 $r$ 变小 C、决定系数 $R^{2}$ 变小 D、解释变量 $x$ 与响应变量 $y$ 的相关性变强

查看试题解析
11. 若函数 $y = f (x)$ 的图象上至少存在两点，使得函数的图象在两点处的切线互相平行，则称 $y = f (x)$ 为R函数，则下列函数可称为R函数的有（）

A、 $f (x) = x^{2} + s i n x$ B、 $f (x) = x^{2} l n x$ C、 $f (x) = e^{x} - \frac{x^{3}}{3}$ D、 $f (x) = \frac{c o s x}{e^{x}}$

查看试题解析

三、填空题

12. ${(2 x - \frac{1}{x})}^{6}$ 的展开式中 $x^{2}$ 的系数为．

查看试题解析
13. 有两台车床加工同一型号的零件，第一台加工的次品率为5%，第二台加工的次品率为4%，加工出来的零件混放在一起，已知第一､二台车床加工的零件数分别占总数的40%，60%，从中任取一件产品，则该产品是次品的概率是.

查看试题解析
14. 数列 ${a_{n}}$ 中， $a_{1} = 2 ， a_{n + 1} + 2 a_{n} = 0$ ，若其前k项和为86，则 $k =$ ．

查看试题解析
15. 已知双曲线 $C ： \frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0 ， b > 0)$ 经过点 $P (\frac{3 \sqrt{5}}{2} ， 2)$ ，双曲线C的离心率为 $\frac{5}{3}$ ，则双曲线C的焦点到其渐近线的距离为．

查看试题解析

四、解答题

16. 已知在 $△ A B C$ 中， $\cos A = \frac{\sqrt{6}}{3}$ ， $a ， b ， c$ 分别是角 $A ， B ， C$ 所对的边.

(1)、求 $\tan 2 A$ ；

(2)、若 $\sin (\frac{π}{2} + B) = \frac{2 \sqrt{2}}{3}$ ， $c = 2 \sqrt{2}$ ，求 $△ A B C$ 的面积.

查看试题解析
17. 已知数列 ${a_{n}}$ 是公差不为零的等差数列， $a_{1} = 2$ ，且 $a_{1} ， a_{3} ， a_{9}$ 成等比数列.

(1)、求数列 ${a_{n}}$ 的通项公式；

(2)、数列 ${b_{n}}$ 满足 $b_{1} = \frac{1}{2} ， \frac{1}{b_{n}} - \frac{1}{b_{n - 1}} = a_{n}$ ，求数列 ${b_{n}}$ 的前 $n$ 项和 $S_{n}$ .

查看试题解析
18. 如图①，在等腰直角三角形 $A B C$ 中， $∠ A = 9 0^{∘} ， A B = 3 ， D ， E$ 分别是 $A C ， B C$ 上的点，且满足 $D E / / A B$ .将 $△ C D E$ 沿 $D E$ 折起，得到如图②所示的四棱锥 $P - A B E D$ .

(1)、设平面 $A B P ∩$ 平面 $D E P = l$ ，证明： $l$ ⊥平面 $A D P$ ；

(2)、若 $P A = \sqrt{5} ， D E = 2$ ，求直线 $P D$ 与平面 $P E B$ 所成角的正弦值.

查看试题解析
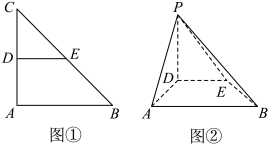19. 已知函数 $f (x) = e^{x} + a x$ （ $a \in R$ ， e为自然对数的底数）.

(1)、讨论函数 $f (x)$ 的单调性；

(2)、求函数 $f (x)$ 的极值的最大值.

查看试题解析
20. 甲乙两人进行乒乓球比赛，经过以往的比赛分析，甲乙对阵时，若甲发球，则甲得分的概率为 $\frac{3}{5}$ ，若乙发球，则甲得分的概率为 $\frac{1}{3}$ .该局比赛甲乙依次轮换发球权(甲先发球)，每人发两球后轮到对方进行发球.

(1)、求在前4球中，甲领先的概率；

(2)、12球过后，双方战平(6：6)，已知继续对战奇数球后，甲率先取得11分获得胜利(获胜要求净胜2分及以上).设净胜分为 $X$ (甲，乙的得分之差)，求 $X$ 的分布列.

查看试题解析
21. 已知椭圆 $C$ ： $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的左、右焦点分别为 $F_{1}$ ， $F_{2}$ ，点 $M (0 ， 2)$ 是椭圆 $C$ 的一个顶点， $△ F_{1} M F_{2}$ 是等腰直角三角形．

(1)、求椭圆 $C$ 的标准方程；

(2)、过点 $M$ 分别作直线 $M A$ ， $M B$ 交椭圆于A ， $B$ 两点，设两直线 $M A$ ， $M B$ 的斜率分别为 $k_{1}$ ， $k_{2}$ ，且 $k_{1} + k_{2} = 8$ ，证明：直线 $A B$ 过定点．

查看试题解析