广东省惠州市2022-2023学年高一下学期期末数学试题

试卷更新日期：2023-08-18 类型：期末考试

进入出卷网下载

一、单选题

1. 已知 $z = 2 + i$ ，则 $\frac{1 + i}{z} =$ （）

A、 $1 + i$ B、 $1 - i$ C、 $\frac{3}{5} + \frac{1}{5} i$ D、 $\frac{1}{5} + \frac{1}{5} i$

查看试题解析
2. “幸福感指数”是指某个人主观地评价他对自己目前生活状态的满意程度的指标，常用区间 $[0 ， 10]$ 内的一个数来表示，该数越接近10表示满意程度越高，现随机抽取7位小区居民，他们的幸福感指数分别为5，6，7，8，9，5，4，则这组数据的第60百分位数是（）

A、7 B、7.5 C、8 D、9

查看试题解析
3. 若空间三条直线a ， b ， c满足a⊥b ， b $∥$ c ，则直线a与c（）

A、一定平行 B、一定垂直 C、一定是异面直线 D、一定相交

查看试题解析
4. 在 $△ A B C$ 中，已知 $b^{2} + c^{2} - a^{2} = b c$ ，且 $2 c o s B s i n C = s i n A$ ，则该三角形的形状是（）

A、直角三角形 B、等腰三角形 C、等边三角形 D、钝角三角形

查看试题解析
5. 已知点 $A (1 ， 1)$ ， $B (0 ， 2)$ ， $C (- 1 ， - 1)$ ．则 $\vec{A B}$ 在 $\vec{B C}$ 上的投影向量为（）

A、 $(\frac{\sqrt{10}}{5} ， \frac{3 \sqrt{10}}{5})$ B、 $(- \frac{\sqrt{10}}{5} ， - \frac{3 \sqrt{10}}{5})$ C、 $(\frac{1}{5} ， \frac{3}{5})$ D、 $(- \frac{1}{5} ， - \frac{3}{5})$

查看试题解析
6. 如图所示，一个物体被两根轻质细绳拉住，且处于平衡状态，已知两条绳上的拉力分别是 $F_{1}$ ， $F_{2}$ ，且 $F_{1}$ ， $F_{2}$ 与水平夹角均为 $45 °$ ， $| F_{1} | = | F_{2} | = 10 \sqrt{2} N$ ，则物体的重力大小为（）

A、 $20 N$ B、 $10 \sqrt{2} N$ C、 $10 N$ D、 $5 \sqrt{2} N$

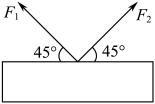查看试题解析
7. 已知圆台的上、下底面的圆周都在半径为2的球面上，圆台的下底面过球心，上底面半径为1，则圆台的体积为（）

A、 $\frac{5 \sqrt{3}}{3} π$ B、 $5 \sqrt{3} π$ C、 $\frac{7 \sqrt{3}}{3} π$ D、 $7 \sqrt{3} π$

查看试题解析
8. 已知函数 $f (x) = 2 c o s (ω x - \frac{π}{3}) + 1$ ，（ $ω > 0$ ）的图象在区间 $(0 ， 2 π)$ 内至多存在3条对称轴，则 $ω$ 的取值范围是（）

A、 $(0 ， \frac{5}{3}]$ B、 $(\frac{2}{3} ， \frac{5}{3}]$ C、 $[\frac{7}{6} ， \frac{5}{3})$ D、 $[\frac{5}{3} ， + \infty)$

查看试题解析

二、多选题

9. 如果 $\vec{a} ， \vec{b}$ 是两个单位向量，则下列结论中正确的是（）

A、 $\vec{a} = \vec{b}$ B、 $\vec{a} = \pm \vec{b}$ C、 ${\vec{a}}^{2} = {\vec{b}}^{2}$ D、 $| \vec{a} | = | \vec{b} |$

查看试题解析
10. 下列说法正确的是（）

A、数据1，2，3，3，4，5的平均数和中位数相同 B、数据6，5，4，3，3，3，2，2，1的众数为3 C、有甲、乙、丙三种个体按3：1：2的比例分层抽样调查，如果抽取的甲个体数为9，则样本容量为30 D、甲组数据的方差为4，乙组数据为5，6，9，10，5，则这两组数据中较稳定的是乙组

查看试题解析
11. 函数 $f (x) = A s i n (ω x + φ)$ （其中 $A > 0$ ， $ω > 0$ ， $| ϕ | < \frac{π}{2}$ ）的图象如图所示，下列说法正确的是（）

A、 $x = \frac{13 π}{12}$ 是它的一条对称轴 B、 $f (x)$ 的增区间为 $[k π - \frac{5 π}{12} ， k π + \frac{π}{12}]$ ， $k ∈ Z$ C、函数 $y = f (x + \frac{π}{4})$ 为奇函数 D、若 $f (\frac{α}{2}) = - \frac{1}{3}$ ， $a \in (\frac{π}{2} ， \frac{3}{2} π)$ ，则 $s i n α = \frac{2 \sqrt{6} - 1}{6}$

查看试题解析
12. 如图，点 $M$ 是棱长为 $1$ 的正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中的侧面 $A D D_{1} A_{1}$ 上的一个动点（包含边界），则下列结论正确的是（）

A、有无数个点 $M$ 满足 $C M ⊥ A D_{1}$ B、当点 $M$ 在棱 $D D_{1}$ 上运动时， $M A + M B_{1}$ 的最小值为 $\sqrt{3} + 1$ C、若 $M B_{1} = \sqrt{2}$ ，则动点 $M$ 的轨迹长度为 $\frac{π}{2}$ D、在线段 $A D_{1}$ 上存在点 $M$ ，使异面直线 $M B_{1}$ 与 $C D$ 所成的角是 $3 0^{∘}$

查看试题解析

三、填空题

13. 在复数范围内，方程 $4 x^{2} + 8 = 0$ 的解为．

查看试题解析
14. 侧面均为面积为4的正方形的正三棱柱的表面积为．

查看试题解析
15. 将 $y = f (x)$ 的图像向左平移 $\frac{π}{4}$ 个单位，再向上平移1个单位之后，可得 $y = s i n 2 x$ 的图像，则 $f (\frac{π}{2}) =$ ．

查看试题解析
16. 古希腊数学家托勒密在他的名著《数学汇编》里给出了托勒密定理，即圆的内接凸四边形的两对对边乘积的和等于两条对角线的乘积．已知AC，BD为圆的内接四边形ABCD的两条对角线，sin∠CBD：sin∠BDC：sin∠BAD=1：1： $\sqrt{3}$ ， AC=4，则△ABD面积的最大值为．

查看试题解析

四、解答题

17. 如图，在正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中， $E$ 是棱 $D D_{1}$ 的中点．

(1)、试判断直线 $B D_{1}$ 与平面 $A C E$ 的位置关系，并说明理由；

(2)、若正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 的棱长为2，求点 $B$ 到平面 $A B_{1} C$ 的距离．

查看试题解析
18. 已知向量 $\vec{a} = (s i n 2 x ， c o s 2 x)$ ， $\vec{b} = (\frac{\sqrt{2}}{2} ， \frac{\sqrt{2}}{2})$ ，设函数 $f (x) = \vec{a} \cdot \vec{b}$ ， $x \in R$ ．

(1)、求函数 $f (x)$ 的最小正周期及对称中心；

(2)、求函数 $f (x)$ 的单调递减区间．

查看试题解析
19. 某企业生产某批产品按产品质量（单位：g）从高到低依比例划定A ， B ， C ， D ， E五个等级，A等级优于B等级，B等级优于C等级，C等级优于D等级，D等级优于E等级．其中A等级产品占该批产品的12%，B等级产品占该批产品的32%，C等级产品占该批产品的37%，D等级产品占该批产品的15%，E等级产品占该批产品的4%．现从该批产品中随机抽取100件产品对其质量进行分析，并绘制出如图所示的频率分布直方图，其中 $5 a = 2 b$ ．

(1)、求图中a ， b的值；

(2)、根据频率分布直方图，估计企业生产的该批产品的质量的平均数（同一组的值用该组区间的中点值作为代表）；

(3)、用样本估计总体的方法，估计该批产品中C等级及以上等级的产品质量至少为多少g？

查看试题解析
20. 如图，在四棱锥 $P - A B C D$ 中，底面 $A B C D$ 为正方形，侧面 $P A D$ 是正三角形，侧面 $P A D ⊥$ 底面 $A B C D$ ， $M$ 是 $P D$ 的中点．

(1)、求证： $A M ⊥$ 平面 $P C D$ ；

(2)、求侧面 $P B C$ 与底面 $A B C D$ 所成二面角的余弦值．

查看试题解析
21. $△ A B C$ 的内角 $A ， B ， C$ 的对边分别为 $a ， b ， c$ ，且 $c o s (A - B) = \sqrt{3} s i n B - c o s C$ ．

(1)、求 $A$ ；

(2)、若 $△ A B C$ 为锐角三角形， $b = 2$ ，求 $△ A B C$ 周长的取值范围．

查看试题解析
22. 已知函数 $y = f (x)$ ， $x \in D$ ，如果对于定义域D内的任意实数x，对于给定的非零常数P，总存在非零常数T，恒有 $f (x + T) < P \cdot f (x)$ 成立，则称函数 $f (x)$ 是D上的P级递减周期函数，周期为T；若恒有 $f (x + T) = P \cdot f (x)$ 成立，则称函数 $f (x)$ 是D上的P级周期函数，周期为T.

(1)、判断函数 $f (x) = x^{2} + 3$ 是R上的周期为1的2级递减周期函数吗，并说明理由？

(2)、已知 $T = \frac{π}{2}$ ， $y = f (x)$ 是 $[0 ， + ∞)$ 上的P级周期函数，且 $y = f (x)$ 是 $[0 ， + ∞)$ 上的严格增函数，当 $x \in [0 ， \frac{π}{2})$ 时， $f (x) = s i n x + 1$ .求当 $x \in [\frac{π}{2} n ， \frac{π}{2} (n + 1)) (n \in N^{*})$ 时，函数 $y = f (x)$ 的解析式，并求实数P的取值范围；

(3)、是否存在非零实数k，使函数 $f (x) = {(\frac{1}{2})}^{x} \cdot c o s k x$ 是R上的周期为T的T级周期函数？请证明你的结论.

查看试题解析