上海市崇明区2022-2023学年高二下学期期末数学试题

试卷更新日期：2023-08-18 类型：期末考试

进入出卷网下载

一、填空题

1. 已知直线l经过点 $A (- 1 ， 1)$ ， $B (2 ， 3)$ ，则它的斜率 $k =$ .

查看试题解析
2. 双曲线 $\frac{x^{2}}{9} - \frac{y^{2}}{16} = 1$ 的渐近线方程是.

查看试题解析
3. 抛物线 $y^{2} = 4 x$ 的焦点到准线的距离是.

查看试题解析
4. 在平面直角坐标系中，点 $P$ 到点 $F_{1} (- 3 ， 0)$ 、 $F_{2} (3 ， 0)$ 的距离之和为 $10$ ，则点 $P$ 的轨迹方程是.

查看试题解析
5. 假设某产品的一个部件来自三个供应商，供货占比分别是 $\frac{1}{2}$ 、 $\frac{1}{6}$ 、 $\frac{1}{3}$ ，而它们的良品率分别是0.92、0.95、0.94．则该部件的总体良品率是．

查看试题解析
6. 已知两点 $P (3 ， 1)$ 、 $Q (5 ， - 3)$ ，则以PQ为直径的圆的方程是.

查看试题解析
7. 已知直线 $l_{1} ： m x - y + 1 = 0$ ，直线 $l_{2} ： 4 x - m y + 2 = 0$ ，若 $l_{1} / / l_{2}$ ，则 $m =$ ．

查看试题解析
8. 从装有3个红球和4个蓝球的袋中，每次不放回地随机摸出一球．记“第一次摸球时摸到红球”为A，“第二次摸球时摸到蓝球”为B，则 $P (B | A) =$ ．

查看试题解析
9. 已知抛物线 $x^{2} = y$ 上的两个不同的点 $A$ 、 $B$ 的横坐标恰好是方程 $x^{2} + 3 x - 2 = 0$ 的根，则直线 $A B$ 的方程为.

查看试题解析
10. 设AB是椭圆Γ的长轴，点C在Γ上，且∠CBA= $\frac{π}{4}$ ，若AB=4，BC= $\sqrt{2}$ ，则Γ的两个焦点之间的距离为．

查看试题解析
11. 赌博有陷阱．某种赌博每局的规则是：赌客先在标记有 $1$ ， $2$ ， $3$ ， $4$ ， $5$ 的卡片中随机摸取一张，将卡片上的数字作为其赌金（单位：元）；随后放回该卡片，再随机摸取两张，将这两张卡片上数字之差的绝对值的 $1.4$ 倍作为其奖金（单位：元）．若随机变量 $ξ_{1}$ 和 $ξ_{2}$ 分别表示赌客在一局赌博中的赌金和奖金，则 $Ε ξ_{1} - Ε ξ_{2} =$ （元）．

查看试题解析
12. 已知实数 $x_{1}$ 、 $x_{2}$ 、 $y_{1}$ 、 $y_{2}$ 满足 $x_{1}^{2} + y_{1}^{2} = 1$ ， $x_{2}^{2} + y_{2}^{2} = 4$ ， $x_{1} x_{2} + y_{1} y_{2} = 0$ ，则 $x_{1} + x_{2}$ 的最大值为.

查看试题解析

二、单选题

13. 若直线 $(a - 1) x + y - 1 = 0$ 与直线 $3 x - a y + 2 = 0$ 垂直，则实数a的值为（）

A、 $\frac{1}{2}$ B、 $\frac{3}{2}$ C、 $\frac{1}{4}$ D、 $\frac{3}{4}$

查看试题解析
14. 某校高中三年级1600名学生参加了区第二次高考模拟统一考试，已知数学考试成绩X服从正态分布 $N (100 ， σ^{2})$ （试卷满分为150分），统计结果显示，数学考试成绩在80分到120分之间的人数约为总人数的 $\frac{3}{4}$ ，则此次统考中成绩不低于120分的学生人数约为（）

A、200 B、150 C、250 D、100

查看试题解析
15. 已知A ， B为平面内两定点，过该平面内动点M作直线AB的垂线，垂足为N.若 ${\vec{M N}}^{2} = - \frac{1}{2} \vec{A N} \cdot \vec{N B}$ ，则动点M的轨迹是（）

A、圆 B、椭圆 C、抛物线 D、双曲线

查看试题解析
16. 将函数 $y = - x^{3} + x$ ， $x \in [0 ， 1]$ 的图象绕点 $(1 ， 0)$ 顺时针旋转 $θ$ 角（ $0 < θ < \frac{π}{2}$ ）得到曲线C ，若曲线C仍是一个函数的图形，则 $θ$ 的最大值为（）

A、 $a r c t a n \frac{1}{2}$ B、 $\frac{π}{6}$ C、 $\frac{π}{4}$ D、 $a r c t a n 2$

查看试题解析

三、解答题

17. 从4名男生和2名女生中任选3人参加演讲比赛，设随机变量X表示所选3人中女生的人数，求：

(1)、“所选3人中女生人数 $X \leq 1$ ”的概率；

(2)、X的期望与方差.

查看试题解析
18. 已知直线l： $y = k x (k \neq 0)$ 与圆C： $x^{2} + y^{2} - 2 x - 3 = 0$ 相交于A、B两点．

(1)、若 $| A B | = \sqrt{13}$ ，求k；

(2)、在x轴上是否存在点M ，使得当k变化时，总有直线MA、MB的斜率之和为0，若存在，求出点M的坐标；若不存在，说明理由．

查看试题解析
19. 某公园有一块如图所示的区域OACB ，该场地由线段OA ， OB ， AC及曲线段BC围成；经测量， $∠ A O B = 90 °$ ， $O A = O B = 100$ 米，曲线段BC是以OB为对称轴的抛物线的一部分，点C到OA ， OB的距离都是50米；现拟在该区域建设一个矩形游乐场OEDF ，其中点D在线段AC或曲线段BC上，点E ， F分别在线段OA ， OB上，且该游乐场最短边长不低于25米；设 $D F = x$ 米，游乐场的面积为S平方米；

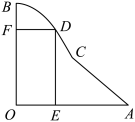(1)、以点O为原点，试建立平面直角坐标系，求曲线段BC的方程；

(2)、求面积S关于x的函数解析式 $S = f (x)$ ；

(3)、试确定点D的位置，使得游乐场的面积S最大（结果精确到0.1米）；

查看试题解析
20. 已知椭圆 $Γ ： \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的离心率是 $\frac{1}{2}$ ，其左、右焦点分别为 $F_{1}$ 、 $F_{2}$ ，过点 $B (0 ， b)$ 且与直线 $B F_{2}$ 垂直的直线交 $x$ 轴负半轴于 $D$ .

(1)、设 $b = 2 \sqrt{3}$ ，求 $a$ 的值；

(2)、求证： $2 \vec{F_{1} F_{2}} + \vec{F_{2} D} = \vec{0}$ ；

(3)、设 $a = 2$ ，过椭圆Γ右焦点 $F_{2}$ 且不与坐标轴垂直的直线 $l$ 与椭圆 $Γ$ 交于 $P$ 、 $Q$ 两点，点 $M$ 是点 $P$ 关于 $x$ 轴的对称点，在 $x$ 轴上是否存在一个定点 $N$ ，使得 $M$ 、 $Q$ 、 $N$ 三点共线？若存在，求出点 $N$ 的坐标；若不存在，说明理由.

查看试题解析
21. 已知函数 $f (x) = \frac{1}{2} x^{2} - (a + 1) x + a l n x$ .（其中 $a$ 为常数）

(1)、若 $a = - 2$ ，求曲线 $y = f (x)$ 在点 $(2 ， f (2))$ 处的切线方程；

(2)、当 $a < 0$ 时，求函数 $y = f (x)$ 的最小值；

(3)、当 $0 \leq a < 1$ 时，试讨论函数 $y = f (x)$ 的零点个数，并说明理由.

查看试题解析