陕西省安康市2022-2023学年高二下册数学文科期末试卷
试卷更新日期:2023-08-18 类型:期末考试
一、单选题
-
1. 已知集合 , , 则( )A、 B、 C、 D、2. 复数的虚部为( )A、 B、2 C、 D、3. 已知 , , , 则( )A、 B、 C、 D、4. 坐标轴与圆的交点个数为( )A、1 B、2 C、3 D、45. 如图,这是一个落地青花瓷,其外形被称为单叶双曲面,可以看成是双曲线C:的一部分绕其虚轴所在直线旋转所形成的曲面.若该花瓶横截面圆的最小直径为8 , 瓶高等于双曲线C的虚轴长,则该花瓶的瓶口直径为( )
 A、 B、24 C、32 D、6. 执行如图所示的程序框图,则输出的( )
A、 B、24 C、32 D、6. 执行如图所示的程序框图,则输出的( ) A、6 B、12 C、20 D、307. 将函数()的图象向右平移1个单位长度后,得到的图象关于原点对称,则的最小值为( )A、 B、1 C、2 D、48. 在正方体中, , 分别是 , 的中点,则直线与直线所成角的正切值为( )A、 B、 C、 D、9. 某校为了了解学生的身体素质,对2022届初三年级所有学生仰卧起坐一分钟的个数情况进行了数据统计,结果如下图所示.该校2023届初三学生人数较2022届初三学生人数上升了10%,则下列说法错误的是( )
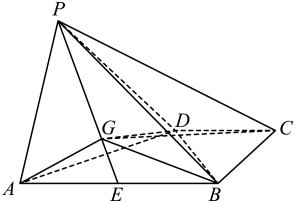
A、6 B、12 C、20 D、307. 将函数()的图象向右平移1个单位长度后,得到的图象关于原点对称,则的最小值为( )A、 B、1 C、2 D、48. 在正方体中, , 分别是 , 的中点,则直线与直线所成角的正切值为( )A、 B、 C、 D、9. 某校为了了解学生的身体素质,对2022届初三年级所有学生仰卧起坐一分钟的个数情况进行了数据统计,结果如下图所示.该校2023届初三学生人数较2022届初三学生人数上升了10%,则下列说法错误的是( )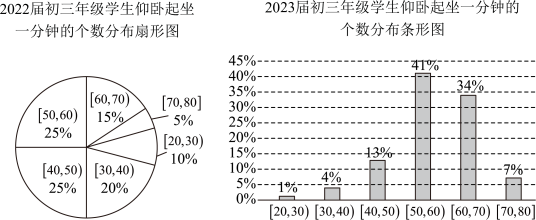 A、该校2022届初三年级学生仰卧起坐一分钟的个数在内的学生人数占70% B、该校2023届初三学生仰卧起坐一分钟的个数在内的学生人数比2022届初三学生仰卧起坐一分钟个数同个数段的学生人数的2倍还多 C、该校2023届初三学生仰卧起坐一分钟的个数和2022届初三学生仰卧起坐一分钟个数的中位数均在内 D、相比2022届初三学生仰卧起坐一分钟个数不小于50的人数,2023届初三学生仰卧起坐一分钟个数不小于50的人数占比增加10. 已知数列满足 , 且(),则( )A、 B、 C、 D、11. 已知某正三棱台的顶点都在半径为5的球面上,若该正三棱台的上、下底边长分别是和 , 则该正三棱台的高为( )A、1 B、2 C、3 D、412. 函数的图象大致为( )A、
A、该校2022届初三年级学生仰卧起坐一分钟的个数在内的学生人数占70% B、该校2023届初三学生仰卧起坐一分钟的个数在内的学生人数比2022届初三学生仰卧起坐一分钟个数同个数段的学生人数的2倍还多 C、该校2023届初三学生仰卧起坐一分钟的个数和2022届初三学生仰卧起坐一分钟个数的中位数均在内 D、相比2022届初三学生仰卧起坐一分钟个数不小于50的人数,2023届初三学生仰卧起坐一分钟个数不小于50的人数占比增加10. 已知数列满足 , 且(),则( )A、 B、 C、 D、11. 已知某正三棱台的顶点都在半径为5的球面上,若该正三棱台的上、下底边长分别是和 , 则该正三棱台的高为( )A、1 B、2 C、3 D、412. 函数的图象大致为( )A、 B、
B、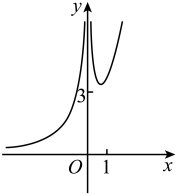 C、
C、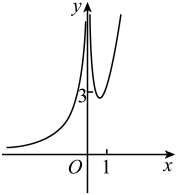 D、
D、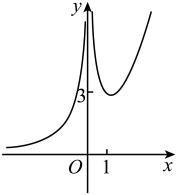
二、填空题
-
13. 已知向量 , 满足 , , 则.14. 函数在区间上的最大值为.15. 盒中装有标有数字1,2,3的卡片各2张,从盒中任意抽取2张,每张卡片被取出的可能性都相等,则抽出的2张卡片上最大的数字是3的概率为.16. 已知 , 为椭圆C:的两个焦点,P,Q为C上关于坐标原点对称的两点,且 , , 则C的离心率为.
三、解答题
-
17. 近日来,ChatGPT的“火”在教育界引发了热议,尤其是在未来课堂上的实践与应用,引起广泛的关注.某学校计划尝试“ChatGPT进课堂”,随机抽取400名家长,对“ChatGPT”的了解情况进行了问卷调查,得到如下列联表.已知了解的人数为280,不了解的人数为120.
男家长
女家长
合计
了解
160
不了解
80
合计
(1)、请补充完整上面的列联表,并分别估计该校男、女家长中对“ChatGPT”了解的概率;(2)、判断是否有99.9%的把握认为该校家长对“ChatGPT”的了解情况与性别有关系.附: , 其中.
0.050
0.010
0.001
3.841
6.635
10.828
18. 在中,分别是内角的对边,.(1)、求角的大小;(2)、若 , 求.19. 已知等比数列的前项和为 , 且.(1)、求的通项公式;(2)、设 , 求数列的前项和.