上海市奉贤区2022-2023学年高二下册数学期末试卷

试卷更新日期：2023-08-18 类型：期末考试

进入出卷网下载

一、填空题

1. 过点 $A (- 1 ， - 1) ， B (2 ， 3)$ 的直线的倾斜角为.（用反三角表示）

查看试题解析
2. 在空间直角坐标系中，点 $P (1 ， - 2 ， 3)$ 关于 $x O z$ 平面的对称点的坐标为.

查看试题解析
3. 在 ${(2 x^{2} - \frac{1}{x})}^{5}$ 的展开式中， $x$ 的系数是.

查看试题解析
4. 已知 $f (x) = x e^{x}$ ，则曲线 $y = f (x)$ 在 $x = 0$ 处的切线方程为．

查看试题解析
5. 若数列 ${a_{n}}$ 中的前n项和 $S_{n} = n^{2} - 3 n$ （n为正整数），则数列 ${a_{n}}$ 的通项公式 $a_{n} =$ .

查看试题解析
6. 掷一颗骰子并观察出现的点数.已知出现的点数不超过 $4$ ，则出现的点数是奇数的概率是.

查看试题解析
7. 已知随机变量 $X$ 服从正态分布 $N (1.5 ， σ^{2})$ ，且 $P (1.5 < X \leq 3) = 0.38$ ，则 $P (X < 0) =$ ．

查看试题解析
8. 若数列 ${a_{n}}$ 的通项公式 $a_{n} = {(\frac{1}{3})}^{n - 1}$ （n为正整数）， ${a_{n}}$ 的前n项和是 $S_{n}$ ，则 $\underset{n \to + \infty}{l i m} S_{n} =$ .

查看试题解析
9. 设双曲线 $C_{1} ： \frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0 ， b > 0)$ ，以C₁的实轴为虚轴，以C₁的虚轴为实轴的双曲线C₂叫做C₁的共轭双曲线，通过研究可以得到双曲线C₁和它的共轭双曲线C₂有很多相同的性质，请写出其中的一个性质：.

查看试题解析
10. 某校在高二开展了选课走班的活动，已知该校提供了3门选修课供学生选择，现有5名同学参加选课走班的活动，要求这5名同学每人选修一门课程且每门课程都有人选，则5名同学选课的种数为.

查看试题解析
11. 已知抛物 $C ： y^{2} = 4 x$ 的焦点为F ，准线为l ，点P在C上，直线PF交y轴于点Q ，若 $\vec{P F} = 3 \vec{F Q}$ ，则P到准线l的距离为.

查看试题解析
12. 已知点 $P (x_{0} ， e^{x_{0}})$ 是函数 $y = e^{x}$ 图像上任意一点，点 $Q$ 是曲线 ${(x - e^{4} - 2)}^{2} + y^{2} = 1$ 上一点，则 $P$ 、 $Q$ 两点之间距离的最小值是.

查看试题解析

二、单选题

13. 假设一水渠的横截面曲线是抛物线形，如图所示，它的渠口宽 $A B$ 为2m，渠深 $O C$ 为1.5m，水面 $E F$ 距 $A B$ 为0.5m，则截面图中水面宽 $E F$ 的长度约为（）m.

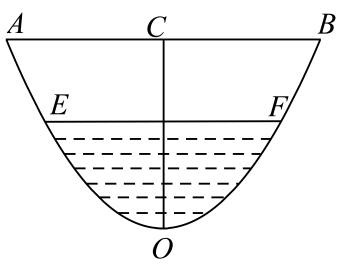A、1.33 B、1.63 C、1.50 D、1.75

查看试题解析
14. 如果 $\bar{A}$ 、 $\bar{B}$ 分别是A、B的对立事件，下列选项中能判断事件A与事件B相互独立的是（）

A、 $P (A \bar{B}) = P (A) \cdot P (\bar{B})$ B、 $P (\bar{A} \bar{B}) = P (A) P (B)$ C、 $P (B | A) = \frac{P (B)}{P (A)}$ D、 $P (B | A) = P (A | B)$

查看试题解析
15. 已知函数 $f (x)$ 的导函数为 $f^{'} (x)$ ，且满足 $f (x) = 2 x f^{'} (1) + l n x$ ，则 $f^{'} (1) =$ （）

A、 $1$ B、 $- \frac{1}{2}$ C、 $- 1$ D、 $e$

查看试题解析
16. 已知数列 ${a_{n}}$ ，设 $m_{n} = \frac{a_{1} + a_{2} + ⋯ + a_{n}}{n}$ （n为正整数）.若 ${a_{n}}$ 满足性质Ω：存在常数c ，使得对于任意两两不等的正整数i、j、k ，都有 $(i - j) m_{k} + (j - k) m_{i} + (k - i) m_{j} = c$ ，则称数列 ${a_{n}}$ 为“梦想数列”.有以下三个命题：
①若数列 ${a_{n}}$ 是“梦想数列”，则常数 $c = 0$ ；
②存在公比不为1的等比数列是“梦想数列”；
③“梦想数列”一定是等差数列.
以上3个命题中真命题的个数是（）个

A、3 B、2 C、1 D、0

查看试题解析

三、解答题

17. 已知在直三棱柱 $A B C - A_{1} B_{1} C_{1}$ 中， $∠ A B C$ 是直角.

(1)、求证：平面 $A_{1} B C$ ⊥平面 $A B B_{1} A_{1}$ ；

(2)、设异面直线 $A_{1} B$ 与 $C_{1} C$ 所成角的大小为 $α$ ，直线 $A_{1} C$ 与平面 $B B_{1} C_{1} C$ 所成角的大小为 $β$ .比较 $α$ 和 $β$ 的大小，并说明理由.

查看试题解析
18. 已知数列 ${b_{n}}$ 是严格增的等比数列， $b_{1} + b_{2} + b_{3} = \frac{21}{8}$ ， $b_{1} b_{2} b_{3} = \frac{1}{8}$ .

(1)、求 ${b_{n}}$ 的通项公式；

(2)、若 $b_{n} = {(\frac{1}{2})}^{a_{n}}$ ，求 $\sum_{i = 1}^{n} a_{3 i - 1}$ .

查看试题解析

19. 某学校研究性学习小组对该校高二学生视力情况进行调查，在高二的全体

1000

名学生中随机抽取了

100

名学生的体检表，并得到如图的频率分布直方图.

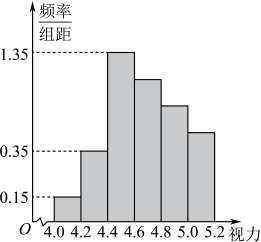
年级名次

是否近视

$1 ∼ 50$

$951 \sim 1000$

近视

$41$

$32$

不近视

$9$

$18$

(1)、若直方图中后四组的频数成等差数列，试估计全年级视力在

5.0

以下的人数；

(2)、学习小组成员发现，学习成绩突出的学生，近视的比较多，为了研究学生的视力与学习成绩是否有关系，对年级名次在

1 ∼ 50

名和

951 \sim 1000

名的学生进行了调查，得到右表中数据，根据

χ^{2}

分布概率表中的数据，能否有

95 %

的把握认为视力与学习成绩有关系？请说明理由；

(3)、在（2）中调查的

100

名学生中，按照分层抽样在不近视的学生中抽取了

9

人进一步调查他们良好的护眼习惯，并且在这

9

人中任取

3

人，记名次在

1 ∼ 50

的学生人数为

X

，求

X

的分布列和数学期望.

附：

$P (χ^{2} ≥ k)$	$0.100$	$0.050$	$0.025$	$0.010$	$0.005$
$k$	$2.706$	$3.841$	$5.624$	$6.635$	$7.879$

$χ^{2} = \frac{n {(a d - b c)}^{2}}{(a + b) (c + d) (a + c) (b + d)}$ .其中 $n = a + b + c + d$ .

查看试题解析

20. 已知椭圆 $\frac{x^{2}}{4} + \frac{y^{2}}{3} = 1$ ，该椭圆与x轴的交点分别是A和B（A在B的左侧），该椭圆的两个焦点分别是F₁和F₂（F₁在F₂的左侧），椭圆与y轴的一个交点是P.

(1)、若P为椭圆的上顶点，求经过点F₁ ， F₂ ， P三点的圆的方程；

(2)、已知点P到过点F₂的直线l的距离是1，求直线l的方程；

(3)、已知椭圆上有不同的两点M、N ，且直线MN不与坐标轴垂直，设直线MA、NB的斜率分别为k₁、k₂ ，求证：“ $\frac{k_{2}}{k_{1}} = 3$ ”是“直线MN经过定点（1，0）”的充要条件.

查看试题解析
21. 对于函数 $y = f (x)$ 的导函数 $y^{'} = f^{'} (x)$ ，若在其定义域内存在实数 $x_{0} ， t$ ，使得 $f (x_{0} + t) = (t + 1) f^{'} (x_{0})$ 成立，则称 $y = f (x)$ 是“跃点”函数，并称 $x_{0}$ 是函数 $y = f (x)$ 的“t跃点”

(1)、若m为实数，函数 $y = s i n x - m$ ， $x \in R$ 是“ $\frac{π}{2}$ 跃点”函数，求m的取值范围；

(2)、若a为非零实数，函数 $y = x^{3} - 2 x^{2} + a x - 12$ ， $x \in R$ 是“2跃点”函数，且在定义域内存在两个不同的“2跃点”，求a的值：

(3)、若b为实数，函数 $y = e^{x} + b x ， x \in R$ 是“1跃点”函数，且在定义域内恰存在一个“1跃点”，求b的取值范围.

查看试题解析