安徽省合肥六校联盟2022-2023学年高一下册数学期末联考试卷

试卷更新日期：2023-08-18 类型：期末考试

进入出卷网下载

一、单选题

1. 若复数 $z$ 满足 $i \cdot z = 3 - 4 i$ ，则 $| z | =$ （）

A、1 B、5 C、7 D、25

查看试题解析
2. $s i n 18 ° c o s 63 ° - s i n 72 ° s i n 117 °$ 的值为（）

A、 $- \frac{\sqrt{2}}{2}$ B、 $\frac{\sqrt{2}}{2}$ C、 $\frac{1}{2}$ D、 $- \frac{1}{2}$

查看试题解析
3. 从装有2个红球和2个黑球的口袋内任取2个球，那么互斥而不对立的两个事件是（）

A、至少有一个黑球与都是黑球 B、至少有一个黑球与都是红球 C、恰有一个黑球与恰有两个黑球 D、至少有一个黑球与至少有一个红球

查看试题解析
4. 已知命题p： $x^{2} - 3 x - 10 > 0$ ，命题q： $x ＞ m^{2} ﹣ m + 3$ ，若 $\neg p$ 是 $\neg q$ 的充分不必要条件，则实数m的取值范围是（）

A、[﹣1，2] B、（﹣∞，﹣1]∪[2，+∞） C、（﹣∞，﹣1）∪（2，+∞） D、（﹣1，2）

查看试题解析
5. 已知 $[x]$ 表示不超过实数 $x$ 的最大整数， $g (x) = [x]$ 为取整函数， $x_{0}$ 是函数 $f (x) = \ln x + x - 4$ 的零点，则 $g (x_{0}) =$ （）

A、4 B、5 C、2 D、3

查看试题解析
6. 设 $m$ ， $n$ 是两条不同的直线， $α$ ， $β$ 是两个不同的平面，下列命题中正确的是（）

A、若 $α ⊥ β$ ， $m \subset α$ ， $n \subset β$ ，则 $m ⊥ n$ B、若 $α // β$ ， $m \subset α$ ， $n \subset β$ ，则 $m // n$ C、若 $m ⊥ n$ ， $m \subset α$ ， $n \subset β$ ，则 $α ⊥ β$ D、若 $m ⊥ α$ ， $m // n$ ， $n // β$ ，则 $α ⊥ β$

查看试题解析
7. 一个电路如图所示，A，B，C，D，E，F为6个开关，其闭合的概率为 $\frac{1}{2}$ ，且是相互独立的，则灯亮的概率是（）

A、 $\frac{1}{64}$ B、 $\frac{55}{64}$ C、 $\frac{1}{8}$ D、 $\frac{1}{16}$

查看试题解析
8. 半正多面体亦称“阿基米德多面体”，是由边数不全相同的正多边形围成的多面体，体现了数学的对称美．二十四等边体就是一种半正多面体，是由正方体切截而成的，它由八个正三角形和六个正方形围成（如图所示），若它所有棱的长都为2，则（）

A、 $B C ⊥$ 平面 $A B E$ B、该二十四等边体的体积为 $\frac{32 \sqrt{2}}{3}$ C、ME与PN所成的角为 $4 5^{∘}$ D、该二十四等边体的外接球的表面积为 $16 π$

查看试题解析

二、多选题

9. 已知向量 $\vec{a} = (1 ， 1)$ ， $\vec{b} = (c o s θ ， s i n θ) (0 \leq θ \leq π)$ ，则下列命题正确的是（）

A、若 $\vec{b} = (\frac{\sqrt{2}}{2} ， \frac{\sqrt{2}}{2})$ ，则 $θ = \frac{π}{4}$ B、向量 $\vec{a}$ 与 $\vec{b}$ 夹角的取值范围是 $[0 ， \frac{3 π}{4}]$ C、与 $\vec{a}$ 共线的单位向量为 $(\frac{\sqrt{2}}{2} ， \frac{\sqrt{2}}{2})$ D、存在 $θ$ ，使得 $| \vec{a} + \vec{b} | = | \vec{a} - \vec{b} |$

查看试题解析
10. 如图为国家统计局公布的2017~2022年全国城镇居民人均可支配收入及人均消费支出统计图，则（）

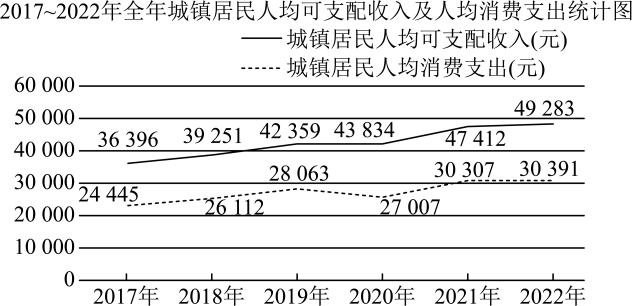A、2017~2022年全国城镇居民人均可支配收入及人均消费支出均呈增长趋势 B、2017~2022年全国城镇居民人均消费支出的中位数为27535 C、2017~2022年全国城镇居民人均可支配收入的极差大于人均消费支出的极差 D、2017~2022年全国城镇居民人均消费支出占人均可支配收入的比例均大于80%

查看试题解析
11. 关于函数f(x)＝sin|x|＋|sin x|的叙述正确的是（）

A、f(x)是偶函数 B、f(x)在区间 $(\frac{π}{2} ， π)$ 单调递增 C、f(x)在[－π，π]有4个零点 D、f(x)的最大值为2

查看试题解析
12. 已知正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ ，则（）

A、直线 $B C_{1}$ 与 $A B_{1}$ 所成的角为60° B、直线 $B C_{1}$ 与 $A_{1} C$ 所成的角为90° C、直线 $B C_{1}$ 平面 $A B B_{1} A_{1}$ 所成的角为45° D、直线 $B C_{1}$ 与平面 $B D D_{1} B_{1}$ 所成的角为45°

查看试题解析

三、填空题

13. 函数 $f (x) = {log}_{2} \sqrt{x} \cdot {log}_{\sqrt{2}} (2 x)$ 的最小值为．

查看试题解析
14. 已知非零向量 $\vec{a} ， \vec{b}$ 满足 $| \vec{a} | = 2 | \vec{b} |$ ，且 $(\vec{a} - \vec{b}) ⊥ \vec{b}$ ，则 $\vec{a}$ 与 $\vec{b}$ 的夹角为．

查看试题解析
15. 在 $△ A B C$ 中，若 $c - a c o s B = (2 a - b) c o s A$ ，则 $△ A B C$ 的形状为.

查看试题解析
16. 从2至8的7个整数中随机取2个不同的数，则这2个数互质的概率为.

查看试题解析

四、解答题

17. 已知一个圆锥的底面半径为 $R$ ，高为 $h$ ，在其内部有一个高为 $x$ 的内接圆柱．

(1)、求圆柱的侧面积；

(2)、求圆柱的侧面积的最大值及此时 $x$ 的值．

查看试题解析
18. 已知向量 $\overset{⇀}{a} = (c o s α ， s i n α)$ ， $\overset{⇀}{b} = (c o s β ， s i n β)$ ， $| \overset{⇀}{a} - \overset{⇀}{b} | = \frac{4 \sqrt{13}}{13}$ .

(1)、求 $c o s (α - β)$ 的值；

(2)、若 $0 < α < \frac{π}{2}$ ， $- \frac{π}{2} < β < 0$ ，且 $s i n β = - \frac{4}{5}$ ，求 $s i n α$ 的值.

查看试题解析
19. 定义在 $[- 4 ， 4]$ 上的奇函数 $f (x)$ ，已知当 $x \in [- 4 ， 0]$ 时， $f (x) = \frac{1}{4^{x}} + \frac{a}{3^{x}}$ ．

(1)、求 $f (x)$ 在 $[0 ， 4]$ 上的解析式；

(2)、若 $\exists x \in [- 2 ， - 1]$ 使不等式 $f (x) \leq \frac{m}{2^{x}} - \frac{1}{3^{x - 1}}$ 成立，求实数m的取值范围．

查看试题解析
20. 在 $△ A B C$ 中，内角 $A ， B ， C$ 的对边分别为 $a ， b ， c$ ，设 $△ A B C$ 的面积为 $S$ ，满足 $a^{2} s i n C = a c c o s B s i n C + S$ .

(1)、求角 $C$ ；

(2)、若 $b s i n C + c s i n B = 6 s i n B$ ，求 $△ A B C$ 周长的最大值.

查看试题解析
21. 随着老年人消费需求从“生存型”向“发展型”转变．消费层次不断提升，“银发经济”成为社会热门话题之一，被各企业持续关注.某企业为了解该地老年人消费能力情况，对该地年龄在 $[60 ， 80)$ 的老年人的年收入按年龄 $[60 ， 70)$ ， $[70 ， 80)$ 分成两组进行分层抽样调查，已知抽取了年龄在 $[60 ， 70)$ 的老年人500人．年龄在 $[70 ， 80)$ 的老年人300人．现作出年龄在 $[60 ， 70)$ 的老年人年收入的频率分布直方图（如下图所示）．

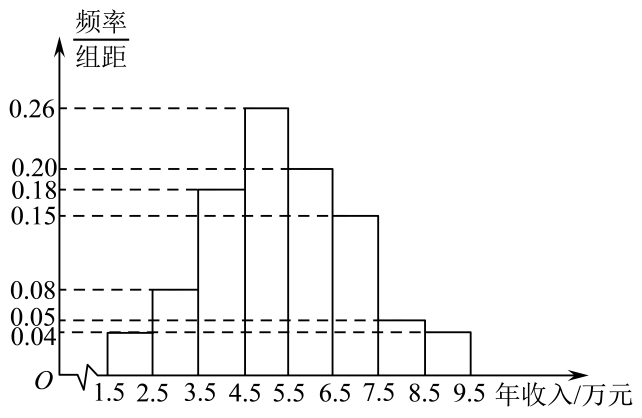(1)、根据频率分布直方图，估计该地年龄在 $[60 ， 70)$ 的老年人年收入的平均数及第95百分位数；

(2)、已知年龄在 $[60 ， 70)$ 的老年人年收入的方差为3，年龄在 $[70 ， 80)$ 的老年人年收入的平均数和方差分别为3.75和1.4，试估计年龄在 $[60 ， 80)$ 的老年人年收入的方差．

查看试题解析
22. 如图， $A B$ 是半球的直径， $O$ 为球心， $A B = 4 ， M ， N$ 依次是半圆 $\overset{⌢}{A B}$ 上的两个三等分点， $P$ 是半球面上一点，且 $P N ⊥ M B$ ，

(1)、证明：平面 $P B M ⊥$ 平面 $P O N$ ；

(2)、若点 $P$ 在底面圆内的射影恰在 $B M$ 上，求二面角 $A - P B - N$ 的余弦值．

查看试题解析