辽宁省鞍山市2022-2023学年高二下册数学期末试卷
试卷更新日期:2023-08-18 类型:期末考试
一、单选题
-
1. 已知集合 , , 则( )A、 B、 C、 D、2. 命题“ , ”的否定是( )A、 , B、 , C、 , D、 ,3. 已知 , ,且 ,则 的最小值为( )A、8 B、 C、9 D、4. 若函数的定义域为 , 值域为 , 则函数的图像可能是( )A、
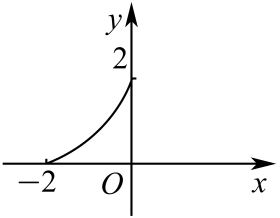 B、
B、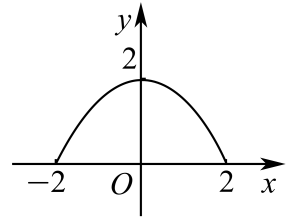 C、
C、 D、
D、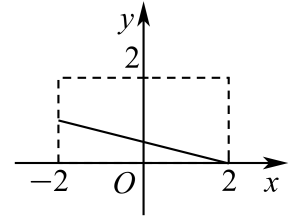 5. 已知 , 则( ).A、 B、 C、 D、6. 已知函数y=f(x+1)的定义域是[-2,3],则y=f(x)的定义域是( )A、[0,5] B、[-1,4] C、[-3,2] D、[-2,3]7. 已知偶函数 的定义域为R,当 时, 单调递增,则 , , 的大小关系是( )A、 B、 C、 D、8. 已知函数是R上的增函数,则a的取值范围是( )A、[-4,0) B、[-4,-2) C、[-4,+∞) D、(-∞,-2)
5. 已知 , 则( ).A、 B、 C、 D、6. 已知函数y=f(x+1)的定义域是[-2,3],则y=f(x)的定义域是( )A、[0,5] B、[-1,4] C、[-3,2] D、[-2,3]7. 已知偶函数 的定义域为R,当 时, 单调递增,则 , , 的大小关系是( )A、 B、 C、 D、8. 已知函数是R上的增函数,则a的取值范围是( )A、[-4,0) B、[-4,-2) C、[-4,+∞) D、(-∞,-2)二、多选题
-
9. 下列函数既是偶函数,在 上又是增函数的是( )A、 B、 C、 D、10. 下列说法正确的是( )A、命题“”的否定是“”. B、命题“”的否定是“” C、“是“”的必要条件. D、“”是“关于的方程有一正一负根”的充要条件11. 下列各组函数中,两个函数是同一函数的有( )A、与 B、与 C、与 D、与12. 下列说法正确的有( )A、的最小值为2 B、已知 , 则的最小值为 C、若正数x,y为实数,若 , 则的最大值为3 D、设x,y为实数,若 , 则的最大值为
三、填空题
-
13. 已知函数的定义域为R , 则实数a的取值范围是 .14. 已知 , 若幂函数为奇函数,且在上是严格减函数,则取值的集合是 .15. 不等式的解集是 , 则不等式的解集为.16. 已知定义域为 的奇函数 ,则 的解集为 .
四、解答题
-
17. 已知集合 .(1)、若 , 求实数m的取值范围;(2)、当集合A变为时,求A的非空真子集的个数;(3)、若 , 求实数m的取值范围.18. 在① , ② , 且 , ③恒成立,且这三个条件中任选一个,补充在下面的问题中,并作答.问题:已知二次函数的图像经过点(1,2), ▲ .(1)、求的解析式;(2)、求在上的值域.19. 已知函数.(1)、当时,证明在区间上的单调递减;(2)、当时,恒成立,求实数的取值范围.20. 近日,随着新冠肺炎疫情在多地零星散发,一些城市陆续发出“春节期间非必要不返乡,就地过年”的倡议.为最大程度减少人员流动,减少疫情发生的可能性,某地政府积极制定政策,决定政企联动,鼓励企业在春节期间留住员工在本市过年并加班追产.为此,该地政府决定为当地某企业春节期间加班追产提供(万元)的专项补贴.企业在收到政府(万元)补贴后,产量将增加到(万件).同时企业生产(万件)产品需要投入成本为(万元),并以每件元的价格将其生产的产品全部售出.注:收益销售金额政府专项补贴成本.(1)、求企业春节期间加班追产所获收益(万元)关于政府补贴(万元)的函数关系式;(2)、当政府的专项补贴为多少万元时,企业春节期间加班追产所获收益最大?