江西省上饶市2022-2023学年高一下册数学期末试卷
试卷更新日期:2023-08-18 类型:期末考试
一、单选题
-
1. 已知 , 是虚数单位,若与互为共轭复数,则( )A、1 B、 C、3 D、2. 已知角的始边在轴的非负半轴上,终边经过点 , 则( )A、 B、 C、 D、3. 设l是直线, 是两个不同的平面,下列命题中正确的是( )A、若 ,则 B、若 ,则 C、若 ,则 D、若 ,则4. 已知 , 则( )A、 B、 C、 D、5. 双塔公园,位于上饶市信州区信江北岸.“双塔”指五桂塔和奎文塔,始建于明清年间,是上饶市历史文化遗存的宝贵财富.某校开展数学建模活动,有建模课题组的学生选择测量五桂塔的高度,为此,他们设计了测量方案.如图,五桂塔垂直于水平面,他们选取了与王桂塔底部在同一水平面上的 , 两点,测得米,在 , 两点观察塔顶点,仰角分别为和 , , 则五桂塔的高度是( )

 A、10米 B、17米 C、25米 D、34米6. 函数的部分图象如图所示,则下列结论正确的是( )
A、10米 B、17米 C、25米 D、34米6. 函数的部分图象如图所示,则下列结论正确的是( ) A、 B、 C、的图象关于点对称 D、的图象关于直线对称7. 如图,已知棱长为的正方体中,点在正方体的棱、、上运动,平面 , 垂足为 , 则点形成图形中的各线段长度之和是( )
A、 B、 C、的图象关于点对称 D、的图象关于直线对称7. 如图,已知棱长为的正方体中,点在正方体的棱、、上运动,平面 , 垂足为 , 则点形成图形中的各线段长度之和是( )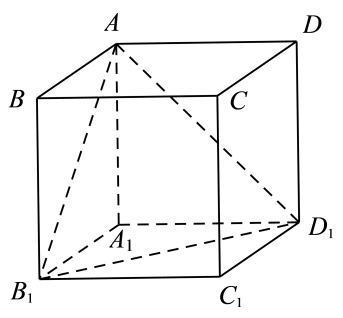 A、2 B、 C、 D、8. 已知函数在上单调,而函数有最大值1,则下列数值可作为取值的是( )A、 B、 C、1 D、2
A、2 B、 C、 D、8. 已知函数在上单调,而函数有最大值1,则下列数值可作为取值的是( )A、 B、 C、1 D、2二、多选题
-
9. 复数 , 是虚数单位,则以下结论正确的是( )A、 B、 C、的虚部为2 D、在复平面内对应点位于第一象限10. 如图,点P在正方体的面对角线上运动,则下列四个结论一定正确的有( )
 A、∥ B、∥面 C、∥面 D、三棱锥的体积不变11. 已知函数的图象向右平移个单位得到函数的图象,函数为偶函数,则的值可以是( )A、 B、 C、 D、12. 在平面直角坐标系中,已知 , , 则下列结论正确的是( )A、的取值范围是 B、当时,在方向上的投影数量的取值范围是 C、的最大值是 D、若 , 且 , 则最大值为2
A、∥ B、∥面 C、∥面 D、三棱锥的体积不变11. 已知函数的图象向右平移个单位得到函数的图象,函数为偶函数,则的值可以是( )A、 B、 C、 D、12. 在平面直角坐标系中,已知 , , 则下列结论正确的是( )A、的取值范围是 B、当时,在方向上的投影数量的取值范围是 C、的最大值是 D、若 , 且 , 则最大值为2三、填空题
-
13. 如图,一个水平放置的平面图形的斜二测直观图是直角梯形 , 且 , , , 则该平面图形的高为.
 14. 已知 , , 则.15. 如图,长方体中, , 则四面体的外接球的体积为.
14. 已知 , , 则.15. 如图,长方体中, , 则四面体的外接球的体积为. 16. 已知是边长为2的等边三角形.如图,将的顶点与原点重合,在轴上,然后将三角形沿着轴正方向滚动,每当顶点再次回落到轴上时,将相邻两个点之间的距离称为“一个周期”,则完成“一个周期”时,顶点的路径长度为.
16. 已知是边长为2的等边三角形.如图,将的顶点与原点重合,在轴上,然后将三角形沿着轴正方向滚动,每当顶点再次回落到轴上时,将相邻两个点之间的距离称为“一个周期”,则完成“一个周期”时,顶点的路径长度为.
四、解答题
-
17. 已知 , , .(1)、若 , 求实数的值;(2)、若 , 求实数的值.18. 设的内角 , , 所对的边分别为 , , , 已知.(1)、求角;(2)、已知 , , 点是边上的点,求线段的最小值.19. 如图,正四棱台中, , , .
 (1)、证明:平面;(2)、若 , 求异面直线与所成的角的余弦值.20. 如图四棱锥中,平面 , 为平行四边形,且 , , , 是棱上的一点, .
(1)、证明:平面;(2)、若 , 求异面直线与所成的角的余弦值.20. 如图四棱锥中,平面 , 为平行四边形,且 , , , 是棱上的一点, . (1)、证明:平面;(2)、求三棱锥的体积.21. 筒车是我国古代发明的一种灌溉工具,因其经济又环保,至今还在农业生产中得到使用(图1).如图2,现有一个半径为4米的筒车按逆时针方向每分钟匀速旋转1圈,筒车的轴心距离水面的高度为2米,若以盛水筒刚浮出水面在点处时为初始时刻,设经过秒后盛水筒到水面的距离为(单位:米)(在水面下则为负数).筒车上均匀分布着12个盛水筒,假设盛水筒在最高处时把水倾倒到水槽上.
(1)、证明:平面;(2)、求三棱锥的体积.21. 筒车是我国古代发明的一种灌溉工具,因其经济又环保,至今还在农业生产中得到使用(图1).如图2,现有一个半径为4米的筒车按逆时针方向每分钟匀速旋转1圈,筒车的轴心距离水面的高度为2米,若以盛水筒刚浮出水面在点处时为初始时刻,设经过秒后盛水筒到水面的距离为(单位:米)(在水面下则为负数).筒车上均匀分布着12个盛水筒,假设盛水筒在最高处时把水倾倒到水槽上. (1)、求函数的表达式;(2)、求第一筒水倾倒的时刻和相邻两个盛水筒倾倒的时间差;(3)、若某一稻田灌溉需水量为100立方米,一个盛水筒倾倒到水槽的水约为0.01立方米,求需要多少小时才能完成该稻田的浇灌.(精确到0.1小时)22. 已知函数.(1)、求函数的单调递增区间;(2)、若 , 存在 , 对任意 , 有恒成立,求的最小值;(3)、若函数在内恰有2023个零点,求与的值.
(1)、求函数的表达式;(2)、求第一筒水倾倒的时刻和相邻两个盛水筒倾倒的时间差;(3)、若某一稻田灌溉需水量为100立方米,一个盛水筒倾倒到水槽的水约为0.01立方米,求需要多少小时才能完成该稻田的浇灌.(精确到0.1小时)22. 已知函数.(1)、求函数的单调递增区间;(2)、若 , 存在 , 对任意 , 有恒成立,求的最小值;(3)、若函数在内恰有2023个零点,求与的值.