【备考2024】高考数学(三角函数版块)细点逐一突破训练:三角函数的值域与最值
试卷更新日期:2023-08-18 类型:二轮复习
一、选择题
-
1. 已知函数 .给出下列结论:
① 的最小正周期为 ;② 是 的最大值;③把函数 的图象上所有点向左平移 个单位长度,可得到函数 的图象.其中所有正确结论的序号是( )
A、① B、①③ C、②③ D、①②③2. 在锐角中,角所对的边为 , 若 , 且 , 则的可能取值为( )A、 B、2 C、 D、3. 已知函数 , , , 在上单调,则的最大值为( ).A、3 B、5 C、6 D、74. 众所周知的“太极图”,其形状如对称的阴阳两鱼互抱在一起,因而也被称为“阴阳鱼太极图”.如图是放在平面直角坐标系中的“太极图”,整个图形是一个圆形,其中黑色阴影区域在y轴右侧部分的边界为一个半圆.给出以下命题:
①在太极图中随机取一点,此点取自黑色阴影部分的概率是;
②当时,直线与黑色阴影部分有公共点;
③黑色阴影部分中一点 , 则的最大值为2.
其中所有正确结论的序号是
A、① B、② C、①③ D、①②5. 已知函数 . 给出以下几个结论:①若对任意 , 均有 , 则的最小值为2;
②若对任意 , 均有 , 则的最小值为5;
③若在区间上的极小值点有且仅有2个,则 .
其中,正确结论的序号是()
A、①② B、①③ C、②③ D、①②③6. 已知函数的部分图像如图所示,将的图像向右平移个单位后,得到函数的图像,若对于任意的 , 则值可以为()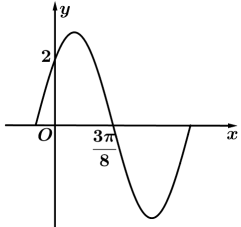 A、 B、 C、 D、7. 已知 , 函数在上单调递增,且对任意 , 都有 , 则的取值范围为( )A、 B、 C、 D、8. 已知函数的图象向左平移个单位长度后得到函数的图象,关于函数 , 下列选项不正确的是( )A、最小正周期为 B、 C、图象的对称中心为 D、当时,取得最大值9. 设 , , 则的最大值是( )A、1 B、 C、 D、210. 若函数在区间内存在唯一的 , 使得 , 则的值不可能是( )A、 B、 C、 D、11. 已知定义在上的函数( )A、若恰有两个零点,则的取值范围是 B、若恰有两个零点,则的取值范围是 C、若的最大值为 , 则的取值个数最多为2 D、若的最大值为 , 则的取值个数最多为3
A、 B、 C、 D、7. 已知 , 函数在上单调递增,且对任意 , 都有 , 则的取值范围为( )A、 B、 C、 D、8. 已知函数的图象向左平移个单位长度后得到函数的图象,关于函数 , 下列选项不正确的是( )A、最小正周期为 B、 C、图象的对称中心为 D、当时,取得最大值9. 设 , , 则的最大值是( )A、1 B、 C、 D、210. 若函数在区间内存在唯一的 , 使得 , 则的值不可能是( )A、 B、 C、 D、11. 已知定义在上的函数( )A、若恰有两个零点,则的取值范围是 B、若恰有两个零点,则的取值范围是 C、若的最大值为 , 则的取值个数最多为2 D、若的最大值为 , 则的取值个数最多为3二、填空题
-
12. 如图,在正方体ABCD﹣A1B1C1D1中,E是AB的中点,F在CC1上,且CF=2FC1 , 点P是侧面AA1D1D(包括边界)上一动点,且PB1∥平面DEF,则tan∠ABP的取值范围为 .
 13. 已知函数 ,则 的最小值是.14. 已知 , 函数在区间上有唯一的最小值-2,则的取值范围为 .15. 若函数的最大值为 , 则常数的值为 .16. 在中, , 则;点是上靠近点的一个三等分点,记 , 则当取最大值时, .17. 设点P在以A为圆心,半径为1的圆弧 上运动(包含B,C两个端点),∠BAC= ,且 ,x+y的取值范围为 .
13. 已知函数 ,则 的最小值是.14. 已知 , 函数在区间上有唯一的最小值-2,则的取值范围为 .15. 若函数的最大值为 , 则常数的值为 .16. 在中, , 则;点是上靠近点的一个三等分点,记 , 则当取最大值时, .17. 设点P在以A为圆心,半径为1的圆弧 上运动(包含B,C两个端点),∠BAC= ,且 ,x+y的取值范围为 . 18. 某地进行老旧小区改造,有半径为60米,圆心角为的一块扇形空置地(如图),现欲从中规划出一块三角形绿地 , 其中在上, , 垂足为 , , 垂足为 , 设 , 则(用表示);当在上运动时,这块三角形绿地的最大面积是.
18. 某地进行老旧小区改造,有半径为60米,圆心角为的一块扇形空置地(如图),现欲从中规划出一块三角形绿地 , 其中在上, , 垂足为 , , 垂足为 , 设 , 则(用表示);当在上运动时,这块三角形绿地的最大面积是. 19. 已知点P在圆上, , , 则的最小值为.20. 已知函数的部分图象如图所示,则时,函数的值域为.
19. 已知点P在圆上, , , 则的最小值为.20. 已知函数的部分图象如图所示,则时,函数的值域为. 21. 已知单位向量满足 , , 则对任意 , 的最小值为.22. 已知向量 , , 满足 , , , 则的最大值是.23. 若向量、的夹角为 , 且 , 则的最大值为.
21. 已知单位向量满足 , , 则对任意 , 的最小值为.22. 已知向量 , , 满足 , , , 则的最大值是.23. 若向量、的夹角为 , 且 , 则的最大值为.三、解答题
-
24. 已知函数f(x)=sin2xsin2x.(1)、讨论f(x)在区间(0,π)的单调性;(2)、证明: ;(3)、设n∈N*,证明:sin2xsin22xsin24x…sin22nx≤ .25. 已知函数
(Ⅰ)求 的最小正周期
(Ⅱ)若 在区间 上的最大值为 ,求 的最小值.
26. 在锐角中,角所对的边分别为 , 且.(1)、求角的大小;(2)、若边 , 边的中点为 , 求中线长的取值范围.27. 已知a,b,c分别为中三内角A,B,C的对边,且 , , D为直线BC上一动点.(1)、求A;(2)、在① , ② , ③这三个条件中任选一个,求线段AD长度的最小值.28. 已知 , , 均为正实数,且.(1)、若 , 求证:;(2)、若 , 求的取值范围.29. 已知 , , 的内角A,B,C所对的,边分别为a,b,c,若的最大值为.(1)、求A;(2)、当 , 时,求的面积.30. 在锐角中,内角A、B、C所对边分别为a、b、c,且 .(1)、求角B;(2)、求的最大值.31. 如图所示,在平面四边形中, , , , 设 . (1)、若 , 求的长;(2)、当为何值时,的面积取得最大值,并求出该最大值.32. 在平面直角坐标系中,圆的参数方程为(θ为参数),以原点为极点,轴的非负半轴为极轴建立极坐标系,曲线的极坐标方程为.(1)、求圆的极坐标方程及曲线的直角坐标方程;(2)、设射线与圆交于异于原点的一点 , 与曲线交于点 , 求与面积之比的最大值.33. 在直角坐标系中,曲线(为参数,常数).以坐标原点为极点,轴非负半轴为极轴建立极坐标系,并在两坐标系中取相同的长度单位.曲线的极坐标方程为 .
(1)、若 , 求的长;(2)、当为何值时,的面积取得最大值,并求出该最大值.32. 在平面直角坐标系中,圆的参数方程为(θ为参数),以原点为极点,轴的非负半轴为极轴建立极坐标系,曲线的极坐标方程为.(1)、求圆的极坐标方程及曲线的直角坐标方程;(2)、设射线与圆交于异于原点的一点 , 与曲线交于点 , 求与面积之比的最大值.33. 在直角坐标系中,曲线(为参数,常数).以坐标原点为极点,轴非负半轴为极轴建立极坐标系,并在两坐标系中取相同的长度单位.曲线的极坐标方程为 .(Ⅰ)若曲线与有公共点,求的取值范围;
(Ⅱ)若 , 过曲线上任意一点作曲线的切线,切点为 , 求的最小值.