【备考2024】高考数学(三角函数版块)细点逐一突破训练:三角函数的周期性1
试卷更新日期:2023-08-18 类型:二轮复习
一、选择题
-
1. 已知函数的一条对称轴为直线 , 一个周期为4,则的解析式可能为( )A、 B、 C、 D、2. 已知 , 关于该函数有下列四个说法:
①的最小正周期为;
②在上单调递增;
③当时,的取值范围为;
④的图象可由的图象向左平移个单位长度得到.
以上四个说法中,正确的个数为( )
A、1 B、2 C、3 D、43. 设函数 在 的图像大致如下图,则f(x)的最小正周期为( )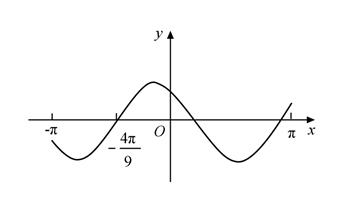 A、 B、 C、 D、4. 已知函数 .给出下列结论:
A、 B、 C、 D、4. 已知函数 .给出下列结论:① 的最小正周期为 ;② 是 的最大值;③把函数 的图象上所有点向左平移 个单位长度,可得到函数 的图象.其中所有正确结论的序号是( )
A、① B、①③ C、②③ D、①②③5. 已知函数()的图象的两个相邻对称中心之间的距离为 , 则( )A、2 B、4 C、8 D、166. 已知函数的最小正周期为 , 且的图象过点 , 则下列结论中正确的是( )A、的最大值为 B、的图象一条对称轴为 C、在上单调递减 D、把的图象向左平移个单位长度,得到函数的图象7. 质点P和Q在以坐标原点O为圆心,半径为1的上逆时针作匀速圆周运动,同时出发.P的角速度大小为 , 起点为与x轴正半轴的交点;Q的角速度大小为 , 起点为射线与的交点.则当Q与P重合时,Q的坐标可以为( )A、 B、 C、 D、8. 下列四个函数中,最小正周期与其余三个函数不同的是( )A、 B、 C、 D、9. 已知函数 , 以下结论错误的是( )A、π是的一个周期 B、在区间单调递减 C、是偶函数 D、在区间恰有两个零点10. 下列函数中最小正周期不是的周期函数为( )A、 B、 C、 D、11. 将函数的图象向左平移个单位,得到函数的图象,若函数在区间上单调递增,则的值可能为( )A、 B、 C、3 D、412. “”是“函数的最小正周期为”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件13. 已知将函数 的图象向右平移 个单位后得到函数 的图象,则 的值为( )A、 B、 C、 D、14. 已知函数 , 则下列说法正确的是( )A、的最小正周期是 B、的值域是 C、在区间上单调递减 D、的图象关于点对称二、填空题
-
15. 函数的非负零点按照从小到大的顺序分别记为 , . ,若 , 则的值可以是 . (写出符合条件的一个值即可)16. 函数的最小正周期为 .17. 设函数相邻两条对称轴之间的距离为 , , 则的最小值为 .18. 已知函数的两个相邻零点之间的距离是 , 则 .19. 已知函数的图象关于直线对称,若对任意 , 总存在 , 使得 , 则的最小值为 , 当取得最小值时,对恒成立,则的最大值为.20. 将函数的图像分别向左、向右各平移个单位长度后,所得的两个函数图象的对称轴重合,则的最小值为.21. 定义运算“★”: .设函数 ,给出下列四个结论:① 是 的最小正周期;② 在 有2个零点;③ 在 上是单调递增函数;④ 的图象可以由 的图象向右平移 个单位长度得到.其中所有正确结论的序号是 .22. 函数的最小正周期是.23. 函数的最小正周期为.24. 已知定义在 上函数 ( )振幅为2,满足 ,且 .则 上 零点个数最少为 .
三、解答题
-
25. 已知函数 .(1)、求 的值;(2)、求 的最小正周期.26. 已知函数.(1)、若 , 求函数的最小正周期;(2)、若图象在内有且仅有一条对称轴,求的取值范围.27. 已知函数 .(1)、当时,求在点处的切线方程;(2)、当时, , 求实数m的取值范围.28. 已知函数 .(1)、求的最小正周期;(2)、若在区间上的最小值为 , 求的最大值.29. 设函数.(1)、求函数的最小正周期;(2)、求函数在上的最小值.30. 已知 , ,(1)、求的最小正周期及单调递减区间;(2)、已知锐角的内角的对边分别为 , 且 , , 求边上的高的最大值.31. 设函数 .(1)、求函数f(x)的最大值和最小正周期;(2)、设A,B,C为 的三个内角, ,且C为锐角, ,a=4,求c边的长.32. 已知函数 在 处取得最大值.(1)、求函数 的最小正周期;(2)、若 的角 , , 所对的边分别为 , , ,且 , , ,求 .33. 向量 , ,已知函数 ,(1)、求函数 的最小正周期和单调递减区间;(2)、 的内角 的对边分别为 ,其中 ,若锐角 满足 ,且 ,求 的值.