【备考2024】高考数学(三角函数版块)细点逐一突破训练:五点法画三角函数的图象
试卷更新日期:2023-08-18 类型:二轮复习
一、选择题
-
1. 已知函数的图象过点 , , , 且在上仅有1个极值点,则( )A、 B、 C、1 D、-12. 某同学用“五点法”画函数在一个周期内的简图时,列表如下:
0
x
y
0
2
0
-2
0
则的解析式为( )
A、 B、 C、 D、3. 设函数 ( ),若 在 有且仅有5个极值点,则( )A、 在 有且仅有3个极大值点 B、 在 有且仅有4个零点 C、 的取值范围是 D、 在 上单调递增4. 函数( , , )的部分图象如图所示,将的图象上所有点的横坐标扩大到原来的4倍(纵坐标不变),再把所得的图象沿轴向左平移个单位长度,得到函数的图象,则函数的一个单调递增区间为( ) A、 B、 C、 D、5. 如图的曲线就像横放的葫芦的轴截面的边缘线,我们叫葫芦曲线(也像湖面上高低起伏的小岛在水中的倒影与自身形成的图形,也可以形象地称它为倒影曲线),它对应的方程为 其中记 为不超过 的最大整数),且过点 ,若葫芦曲线上一点 到 轴的距离为 ,则点 到 轴的距离为( )
A、 B、 C、 D、5. 如图的曲线就像横放的葫芦的轴截面的边缘线,我们叫葫芦曲线(也像湖面上高低起伏的小岛在水中的倒影与自身形成的图形,也可以形象地称它为倒影曲线),它对应的方程为 其中记 为不超过 的最大整数),且过点 ,若葫芦曲线上一点 到 轴的距离为 ,则点 到 轴的距离为( ) A、 B、 C、 D、6. 用五点法画y=sin x,x∈[0,2π]的图像时,下列哪个点不是关键点( )A、 B、 C、(π,0) D、(2π,0)7. 小明用“五点法”画函数在某一个周期内的图象时列表并填入了部分数据,如下表:
A、 B、 C、 D、6. 用五点法画y=sin x,x∈[0,2π]的图像时,下列哪个点不是关键点( )A、 B、 C、(π,0) D、(2π,0)7. 小明用“五点法”画函数在某一个周期内的图象时列表并填入了部分数据,如下表:0
x
0
2
0
0
请你根据已有信息推算A,的值依次为( )
A、2,2, B、2,2, C、2, , D、2,2,8. 设函数 ( , , )的部分图象如图所示,则 ( ) A、 B、 C、 D、9. 函数 的部分图象如图所示,下列结论中正确的是( )
A、 B、 C、 D、9. 函数 的部分图象如图所示,下列结论中正确的是( ) A、将函数 的图象向右平移 个单位得到函数 的图象 B、函数 的图象关于点 对称 C、函数 的单调递增区间为 D、直线 是函数 图象的一条对称轴10. 已知函数 的部分图像如图所示,记关于 的方程 在区间 上所有解的和为 ,则 ( )
A、将函数 的图象向右平移 个单位得到函数 的图象 B、函数 的图象关于点 对称 C、函数 的单调递增区间为 D、直线 是函数 图象的一条对称轴10. 已知函数 的部分图像如图所示,记关于 的方程 在区间 上所有解的和为 ,则 ( ) A、 B、 C、 D、11. 已知函数 的图象与 轴相邻交点的横坐标相差 ,把函数 的图象沿 轴向左平移 个单位,得到函数 的图象.关于函数 ,下列说法正确的是( )A、在 上是增函数 B、其图象关于直线 对称 C、函数 是奇函数 D、当 时,函数 的值域是12. 用五点法作函数 的图象时,得到如下表格:
A、 B、 C、 D、11. 已知函数 的图象与 轴相邻交点的横坐标相差 ,把函数 的图象沿 轴向左平移 个单位,得到函数 的图象.关于函数 ,下列说法正确的是( )A、在 上是增函数 B、其图象关于直线 对称 C、函数 是奇函数 D、当 时,函数 的值域是12. 用五点法作函数 的图象时,得到如下表格:0
0
4
0
-4
0
则 , , 的值分别为( )
A、4,2, B、4, , C、4,2, D、4, ,13. 已知函数 的定义域为 ,值域为 ,则 的值不可能是( )A、 B、 C、 D、14. 用“五点法”作 的图像时,首先描出的五个点的横坐标是( )A、 B、 C、 D、15. 将函数 的图象向左平移 个单位长度后得到函数 的图象如图所示,则函数 的解析式是( ) A、
A、 B、
B、 C、
C、 D、
D、 16. 已知a是实数,则函数 的图象不可能是( )A、
16. 已知a是实数,则函数 的图象不可能是( )A、 B、
B、 C、
C、 D、
D、 17. 函数 (其中 )的图象如图所示,为了得到 的图象,则只要将 的图象( )
17. 函数 (其中 )的图象如图所示,为了得到 的图象,则只要将 的图象( ) A、向右平移 个单位长度 B、向右平移 个单位长度 C、向左平移 个单位长度 D、向左平移 个单位长度18. 已知函数f(x)=|sin(2x- |,则下列说法中正确的是( )A、函数f(x)的周期是 B、函数f(x)的图象的一条对称轴方程是x= C、函数f(x)在区间[ , ]为减函数 D、函数f(x)是偶函数19. 下列说法正确的是( )A、函数
A、向右平移 个单位长度 B、向右平移 个单位长度 C、向左平移 个单位长度 D、向左平移 个单位长度18. 已知函数f(x)=|sin(2x- |,则下列说法中正确的是( )A、函数f(x)的周期是 B、函数f(x)的图象的一条对称轴方程是x= C、函数f(x)在区间[ , ]为减函数 D、函数f(x)是偶函数19. 下列说法正确的是( )A、函数 的图像关于
的图像关于  对称 .
B、将函数
对称 .
B、将函数  的图像上所有点的横坐标伸长到原来的
的图像上所有点的横坐标伸长到原来的  倍后得到
倍后得到  .
C、命题
.
C、命题  都是假命题,则命题“
都是假命题,则命题“  ”为真命题.
D、
”为真命题.
D、 ,函数
,函数  都不是偶函数.
20. 已知函数 在一个周期内的图像如图所示。若方程 在区间 上有两个不同的实数解 ,则 的值为( )
都不是偶函数.
20. 已知函数 在一个周期内的图像如图所示。若方程 在区间 上有两个不同的实数解 ,则 的值为( ) A、 B、 C、 D、 或21. 如图是函数 的图象,那么( )
A、 B、 C、 D、 或21. 如图是函数 的图象,那么( )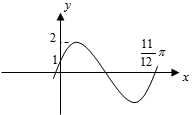 A、 B、 C、 D、22. 已知函数 的周期为 ,将函数 的图象沿着 轴向上平移一个单位得到函数 图象,对任意的 时 恒成立,当 取得最小值时, 的值是( )A、 B、1 C、 D、223. 函数 ( , , )的部分图象如图所示,则该函数的图象可由函数 的图象( )
A、 B、 C、 D、22. 已知函数 的周期为 ,将函数 的图象沿着 轴向上平移一个单位得到函数 图象,对任意的 时 恒成立,当 取得最小值时, 的值是( )A、 B、1 C、 D、223. 函数 ( , , )的部分图象如图所示,则该函数的图象可由函数 的图象( ) A、向左平移 个单位得到 B、向右平移 个单位得到 C、向左平移 个单位得到 D、向右平移 个单位得到24. 已知函数 的部分图象如图所示,则下列判断正确的是( )
A、向左平移 个单位得到 B、向右平移 个单位得到 C、向左平移 个单位得到 D、向右平移 个单位得到24. 已知函数 的部分图象如图所示,则下列判断正确的是( ) A、函数 的最小正周期为 B、函数 的值域为 C、函数 的图象关于直线 对称 D、函数 的图象向左平移 个单位得到函数 的图象25. 函数 的图象与函数 的图象所有交点的横坐标之和等于( )
A、函数 的最小正周期为 B、函数 的值域为 C、函数 的图象关于直线 对称 D、函数 的图象向左平移 个单位得到函数 的图象25. 函数 的图象与函数 的图象所有交点的横坐标之和等于( )
A、18 B、14 C、16 D、1226. 某同学用“五点法”画函数y=Asin(ωx+φ)(A>0,ω>0)在一个周期内简图时,列表如下:ωx+φ
0
π
2π
x
y
0
2
0
﹣2
0
则有( )
A、A=0,ω= ,φ=0 B、A=2,ω=3,φ= C、A=2,ω=3,φ=﹣ D、A=1,ω=2,φ=﹣27. 下列命题正确的是( )A、y=sinx的图象向右平移 个单位得y=cosx的图象 B、y=cosx的图象向右平移 个单位得y=sinx的图象 C、当φ>0时,y=sinx的图象向右平移φ个单位可得y=sin(x+φ)的图象 D、当φ<0时,y=sinx的图象向左平移φ个单位可得y=sin(x﹣φ)的图象28. 将函数y=sinx的图象上每点的横坐标缩小为原来的 (纵坐标不变),再把所得图象向左平移 个单位,得到的函数解析式为( ) A、y=sin(2x+ ) B、y=sin(2x+ ) C、y=sin( + ) D、y=sin( + )29. 用“五点法”画y=sin x,x∈[﹣2π,0]的简图时,正确的五个点应为( )A、(0,0),( ),(π,0),( ,﹣1),(2π,0) B、(0,0),(﹣ ,﹣1),(﹣π,0),(﹣ ,1),(﹣2π,0) C、(0,1),( ,0),(π,1),( ,0),(2π,﹣1) D、(0,﹣1),(﹣ ,0),(﹣π,1),(﹣ ,0),(﹣2π,﹣1)30. 设k∈R,则函数f(x)=sin(kx+ )+k的部分图象不可能是( )A、
(纵坐标不变),再把所得图象向左平移 个单位,得到的函数解析式为( ) A、y=sin(2x+ ) B、y=sin(2x+ ) C、y=sin( + ) D、y=sin( + )29. 用“五点法”画y=sin x,x∈[﹣2π,0]的简图时,正确的五个点应为( )A、(0,0),( ),(π,0),( ,﹣1),(2π,0) B、(0,0),(﹣ ,﹣1),(﹣π,0),(﹣ ,1),(﹣2π,0) C、(0,1),( ,0),(π,1),( ,0),(2π,﹣1) D、(0,﹣1),(﹣ ,0),(﹣π,1),(﹣ ,0),(﹣2π,﹣1)30. 设k∈R,则函数f(x)=sin(kx+ )+k的部分图象不可能是( )A、 B、
B、 C、
C、 D、
D、
二、解答题
-
31. 已知函数f(x)=sin(wx+φ)(w>0,0<φ<π)的周期为π,图象的一个对称中心为( ,0),将函数f(x)图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再将得到的图象向右平移个 单位长度后得到函数g(x)的图象.(1)、求函数f(x)与g(x)的解析式(2)、是否存在x0∈( ),使得f(x0),g(x0),f(x0)g(x0)按照某种顺序成等差数列?若存在,请确定x0的个数,若不存在,说明理由;(3)、求实数a与正整数n,使得F(x)=f(x)+ag(x)在(0,nπ)内恰有2013个零点.