【备考2024】高考数学（三角函数版块）细点逐一突破训练：任意角的三角函数之诱导公式3

试卷更新日期：2023-08-18 类型：二轮复习

进入出卷网下载

一、选择题

1. tan255°=（）

A、 $- 2 - \sqrt{3}$ B、 $- 2 + \sqrt{3}$ C、 $2 - \sqrt{3}$ D、 $2 + \sqrt{3}$

查看试题解析
2. 函数f（x）= $\frac{1}{5}$ sin（x+ $\frac{π}{3}$ ）+cos（x﹣ $\frac{π}{6}$ ）的最大值为（　　）

A、 $\frac{6}{5}$ B、1 C、 $\frac{3}{5}$ D、 $\frac{1}{5}$

查看试题解析
3. 已知函数 $f (x) = \frac{2 t a n \frac{x}{2}}{1 + t a n^{2} \frac{x}{2}}$ ，当 $x \in [0 ， \frac{π}{3}]$ 时， $f (x)$ 的最大值为（）.

A、 $\frac{1}{2}$ B、 $\frac{\sqrt{3}}{3}$ C、 $\frac{\sqrt{3}}{2}$ D、 $\sqrt{3}$

查看试题解析
4. 已知向量 $\vec{a} = (- 1 ， 2)$ ， $\vec{b} = (1 ， 2)$ ，设 $\vec{a}$ ， $\vec{b}$ 的夹角为 $θ$ ，则 $s i n (\frac{3 π}{2} - 2 θ) =$ （）

A、 $- \frac{18}{25}$ B、 $\frac{18}{25}$ C、 $- \frac{7}{25}$ D、 $\frac{7}{25}$

查看试题解析
5. 若直线 $x = 2 \sqrt{2} y - 3 \sqrt{2}$ 与圆 $x^{2} + y^{2} = 4$ 相交于 $A ， B$ 两点， $O$ 为坐标原点，则 $\vec{O A} \cdot \vec{A B} =$ （）

A、 $2 \sqrt{2}$ B、4 C、 $- 2 \sqrt{2}$ D、－4

查看试题解析
6. 已知 $s i n (α - \frac{π}{3}) = \frac{2}{3}$ ，则 $c o s (2 α + \frac{π}{3}) =$ （）

A、 $- \frac{1}{9}$ B、 $\frac{1}{9}$ C、 $- \frac{4 \sqrt{5}}{9}$ D、 $\frac{4 \sqrt{5}}{9}$

查看试题解析
7. 若 $\sin (π - α) = \frac{4}{5}$ ，则 cos2α ＝（）

A、－ $\frac{24}{25}$ B、 $\frac{7}{25}$ C、－ $\frac{7}{25}$ D、 $\frac{24}{25}$

查看试题解析
8. 已知 $(1 ， 2)$ 为角 $α$ 终边上一点，关于 $x$ 的函数 $f (x) = c o s 2 x c o s α - s i n 2 x s i n α$ 有对称轴 $x = m$ ，则 $t a n 2 m =$ （）

A、-2 B、2 C、 $- \frac{1}{2}$ D、 $\frac{1}{2}$

查看试题解析
9. 已知 $f (x) = 1 - 2 c o s^{2} (ω x + \frac{π}{3}) (ω > 0)$ ，则下列判断中，错误的是（）

A、若 $f (x_{1}) = 1$ ， $f (x_{2}) = - 1$ ，且 ${| x_{1} - x_{2} |}_{m i n} = π$ ，则 $ω = 2$ B、存在 $ω \in (0 ， 2)$ ，使得 $f (x)$ 的图像右移 $\frac{π}{6}$ 个单位长度后得到的图像关于 $y$ 轴对称 C、若 $f (x)$ 在 $[0 ， 2 π]$ 上恰有7个零点，则 $ω$ 的取值范围为 $[\frac{41}{24} ， \frac{47}{24}]$ D、若 $f (x)$ 在 $[- \frac{π}{6} ， \frac{π}{4}]$ 上单调递增，则 $ω$ 的取值范围为 $(0 ， \frac{2}{3}]$

查看试题解析
10. 已知 $c o s (\frac{π}{2} + α) + 3 c o s (α - π) = 0$ ，则 $\frac{s i n α - s i n^{3} α}{s i n (\frac{π}{2} + α)} =$ （）

A、 $\frac{3}{5}$ B、 $- \frac{3}{5}$ C、 $\frac{3}{10}$ D、 $- \frac{3}{10}$

查看试题解析
11. 已知 $P (1 ， 3)$ 为角 $α$ 终边上一点，则 $\frac{2 c o s α c o s (α + \frac{π}{2})}{c o s^{2} α + c o s 2 α} =$ （）

A、 $- \frac{1}{7}$ B、 $- \frac{6}{7}$ C、 $\frac{6}{7}$ D、 $\frac{1}{7}$

查看试题解析
12. $\sin \frac{94}{3} π =$ （）

A、 $\frac{\sqrt{3}}{2}$ B、 $- \frac{\sqrt{3}}{2}$ C、 $\frac{1}{2}$ D、 $- \frac{1}{2}$

查看试题解析

二、填空题

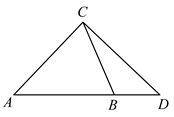
13. 在平面直角坐标系xOy中，角α与角β均以Ox为始边，它们的终边关于y轴对称，若sinα= $\frac{1}{3}$ ，则sinβ= ．

查看试题解析
14. 在平面直角坐标系xOy中，角α与角β均以Ox为始边，它们的终边关于y轴对称，若sinα= $\frac{1}{3}$ ，则cos（α﹣β）= ．

查看试题解析
15. 已知 $\sin x = \frac{3}{5}$ ， $x \in (\frac{π}{2} ， π)$ ，则cos(π﹣x)=.

查看试题解析
16. 曲线 $y = e^{x} + x^{2} - \frac{2}{3} x$ 在 $x = 0$ 处的切线的倾斜角为 $α$ ，则 $\sin (2 α + \frac{π}{2}) =$ ．

查看试题解析
17. 若 $\sin (α + \frac{π}{4}) = \frac{1}{3}$ ，则 $\sin 2 α =$ .

查看试题解析
18. 已知角 $α$ 的终边经过点 $(- 3, 4)$ ，则 $\cos (\frac{3 π}{2} + α)$ 的值是.

查看试题解析
19. 已知锐角 $△ A B C$ 中， $A B = 6 \cos A$ ， $A C = 2 A B - 2$ ， $\sin \frac{A}{2} = \frac{1}{2}$ ，延长 $A B$ 到点 $D$ ，使 $\sin ∠ B C D = \frac{\sqrt{39}}{26}$ ，则 $S_{△ B C D} =$ .

查看试题解析
20. 在矩形ABCD中，其中 $A B = 3$ ， $A D = 1$ ，AB上的点E满足 $\vec{A E} + 2 \vec{B E} = \vec{0}$ ，F为AD上任意一点，则 $\vec{E B} \cdot \vec{B F} =$ .

查看试题解析
21. 某参考辅导书上有这样的一个题：△ $A B C$ 中， $\tan A$ 与 $\tan B$ 方程 $x^{2} - 3 x - 1 = 0$ 的两个根，则 $\tan C$ 的值为（）
A． $- \frac{3}{2}$ B． $\frac{3}{2}$ C． $- \frac{1}{2}$ D． $\frac{1}{2}$

你对这个题目的评价是.(用简短语句回答)

查看试题解析
22. 下列命题中正确命题的序号是..
①若 $sin α = 3 cos α$ ，则 $tan (π + 2 α) = - \frac{3}{4}$ ；

②设 $a > 0, b > 0$ ，且 $a + b = 1$ ，则 $\frac{4}{a} + \frac{1}{b}$ 的最大值为9；

③ $\int_{1}^{2} (\frac{1}{x} + 2 x) d x = m$ ，则 ${(x - \frac{2}{x})}^{4 e^{(m - 3)}}$ 展开式中的常数项为1120；

④对任意 $x \in R$ ，都有 $x^{2} - 2 x + 3 ⩾ 0$ 的否定为：存在 $x_{0} \in R$ ，使得 $x_{0}^{2} - 2 x_{0} + 3 ⩽ 0.$

查看试题解析
23. 已知 $θ$ 为第二象限角，且 $\sin (\frac{θ}{2} + \frac{π}{4}) = \frac{3 \sqrt{10}}{10}$ ，则 $\tan θ =$ .

查看试题解析
24. 曲线 $y = l n x - \frac{2}{x}$ 在 $x = 1$ 处的切线的倾斜角为 $α$ ，则 $s i n (α + \frac{π}{2}) =$ .

查看试题解析

三、解答题

25. 设函数f（x）=sin（ωx﹣ $\frac{π}{6}$ ）+sin（ωx﹣ $\frac{π}{2}$ ），其中0＜ω＜3，已知f（ $\frac{π}{6}$ ）=0．

（Ⅰ）求ω；
（Ⅱ）将函数y=f（x）的图象上各点的横坐标伸长为原来的2倍（纵坐标不变），再将得到的图象向左平移 $\frac{π}{4}$ 个单位，得到函数y=g（x）的图象，求g（x）在[﹣ $\frac{π}{4}$ ， $\frac{3 π}{4}$ ]上的最小值．

查看试题解析
26. 已知向量 $\vec{a} = (\sqrt{3} \sin x ， \cos x)$ ， $\vec{b} = (\cos x ， \cos x)$ .

(1)、若 $\vec{a} // \vec{b}$ ，且 $x \in (- π ， 0)$ ，求 $x$ 的值；

(2)、若函数 $f (x) = 2 \vec{a} \cdot \vec{b} - 1$ ，且 $f (\frac{x}{2}) = \frac{1}{3}$ ，求 $\sin (2 x - \frac{π}{6})$ 的值.

查看试题解析
27. 已知 $\tan (α + π) = 3$ .

(1)、求 $\frac{\tan 2 α}{\tan (2021 π - α)}$ 的值；

(2)、求 $\frac{\sin 2 α + \cos^{2} α}{2 + \sin^{2} α}$ 值.

查看试题解析
28. 在 $△ A B C$ 中，角A ， B ， C的对边分别为a ， b ， c ，且 $10 \sin^{2} \frac{A + C}{2} = 7 - \cos 2 B$ ，

(1)、求角B的大小；

(2)、已知点D满足 $\vec{B D} = \frac{1}{4} \vec{B C}$ ，且 $A B > B D$ ，若 $S_{△ A B D} = \frac{3 \sqrt{3}}{4}$ ， $A D = \sqrt{7}$ ，求AC．

查看试题解析
29. 已知 $△ A B C$ 的三个内角A ， B ， C的对边分别为a ， b ， c ， $a + c = 3$ ， $\frac{\cos C}{\cos B} = \frac{2 a - c}{b}$ ．

(1)、求角B的大小；

(2)、若 $a < b$ ， $b = 2$ ，求 $\cos (A + \frac{π}{6})$ 的值．

查看试题解析
30. 如图，在平面四边形ABCD中， $B C =1， ∠ A B C = 90^{°} ， ∠ B C D = 60^{°}$ ， $∠ B A D = 75^{°}$ ．

(1)、若 $∠ C B D = 30^{°}$ ，求三角形ABD的面积；

(2)、若 $A D = \frac{\sqrt{6} - \sqrt{2}}{2} ，$ 求 $∠ C B D$ 的大小．

查看试题解析
31. 已知 $△ A B C$ 的内角 $A$ ， $B$ ， $C$ 所对的边分别是 $a$ ， $b$ ， $c$ ，若 $\sin (A + C) = 8 \sin^{2} \frac{B}{2}$ ．

(1)、求 $\cos B$ ；

(2)、若 $a + c = 6$ ， $△ A B C$ 的面积为2，求 $b$ ．

查看试题解析
32. 在 $△ A B C$ 中，角 $A ， B ， C$ 的对边分别为 $a ， b ， c$ ，且 $cos 2 A = 1 + 3 cos (B + C)$

(1)、求角 $A$ 的值；

(2)、点 $D$ 在线段 $A C$ 上， $B D = B C ， cos ∠ A B D = \frac{13}{14}$ 且 $A C = 5$ ，求边长 $B D .$

查看试题解析
33. 在① $\cos C + (\cos A - \sqrt{3} \sin A) \cos B = 0$ ，② $\cos 2 B - 3 \cos (A + C) = 1$ ，③ $b \cos C + \frac{\sqrt{3}}{3} c \sin B = a$ 这三个条件中任选一个，补充在下面问题中.
问题：在 $△ A B C$ 中，角 $A$ 、 $B$ 、 $C$ 对应的边分别为 $a$ 、 $b$ 、 $c$ ，若 $a + c = 1$ ， ▲ ，求角 $B$ 的值和 $b$ 的最小值.

查看试题解析
34. 在① $b ＝ \sqrt{3} a$ ；② $a = 3 \cos B$ ；③ $a \sin C = 1$ 这三个条件中任选一个，补充在下面问题中．若问题中的三角形存在，求该三角形面积的值；若问题中的三角形不存在，说明理由．
问题：是否存在 $△ A B C$ ，它的内角 $A, B, C$ 的对边分别为 $a, b, c$ ，且 $\sin B - \sin (A - C) = \sqrt{3} \sin C$ ， $c = 3$ ▲ ？

查看试题解析
35. 如图，在四边形 $A B C D$ 中， $A B // C D$ ， $A B = 2 \sqrt{6}$ ， $C D = \sqrt{6}$ ， $\cos A = \frac{\sqrt{6}}{3}$ ， $\cos ∠ A D B = \frac{1}{3}$ .

(1)、求 $\cos ∠ B D C$ ；

(2)、求 $B C$ 的长.

查看试题解析