【备考2024】高考数学（三角函数版块）细点逐一突破训练：任意角的三角函数之诱导公式2

试卷更新日期：2023-08-18 类型：二轮复习

进入出卷网下载

一、选择题

1. 下图是函数y= sin(ωx+φ)的部分图像，则sin(ωx+φ)= （）

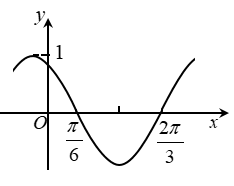
A、 $sin(x + \frac{π}{3} ）$ B、 $sin(\frac{π}{3} - 2 x)$ C、 $cos(2 x + \frac{π}{6} ）$ D、 $cos(\frac{5 π}{6} - 2 x)$

查看试题解析
2. 已知 $α, β \in R$ ，则“存在 $k \in Z$ 使得 $α = k π + {(- 1)}^{k} β$ ”是“ $\sin α = \sin β$ ”的（）．

A、充分而不必要条件 B、必要而不充分条件 C、充分必要条件 D、既不充分也不必要条件

查看试题解析
3. 已知函数 $f (x) = 2 s i n x + 4 c o s x$ 在 $x = φ$ 处取得最大值，则 $c o s φ =$ （）

A、 $\frac{2 \sqrt{5}}{5}$ B、 $\frac{\sqrt{5}}{5}$ C、 $- \frac{\sqrt{5}}{5}$ D、 $- \frac{2 \sqrt{5}}{5}$

查看试题解析
4. 若 $t a n (α - \frac{π}{12}) = s i n \frac{13 π}{3}$ ，则 $t a n (α - \frac{π}{4}) =$ （）

A、 $- \frac{\sqrt{3}}{9}$ B、 $- \frac{\sqrt{3}}{5}$ C、 $\frac{\sqrt{3}}{9}$ D、 $\frac{\sqrt{3}}{5}$

查看试题解析
5. 已知角 $α$ 在第四象限内， $s i n (2 α + \frac{3 π}{2}) = \frac{1}{2}$ ，则 $s i n α =$ （）

A、 $- \frac{1}{2}$ B、 $\frac{1}{2}$ C、 $\frac{\sqrt{2} - \sqrt{6}}{4}$ D、 $- \frac{\sqrt{3}}{2}$

查看试题解析
6. 已知函数 $f (x) = c o s (\frac{2}{3} x + φ)$ 满足 $f (- \frac{π}{6}) = f (\frac{2 π}{3})$ ，若 $f (x)$ 在 $[0 ， a]$ 至少有两个零点，则实数 $a$ 的最小值为（）

A、 $\frac{3 π}{2}$ B、 $2 π$ C、 $\frac{5 π}{2}$ D、 $3 π$

查看试题解析
7. 下列是函数 $f (x) = 2 s i n (x + \frac{3 π}{4}) s i n (x + \frac{π}{4})$ 图像的对称轴的是（）

A、 $x = \frac{π}{6}$ B、 $x = \frac{π}{4}$ C、 $x = \frac{π}{3}$ D、 $x = \frac{π}{2}$

查看试题解析
8. 设 $c o s x = \frac{1}{3}$ ，则 $s i n (x - \frac{π}{2}) =$ （）

A、 $\frac{1}{3}$ B、 $- \frac{1}{3}$ C、 $\frac{2 \sqrt{2}}{3}$ D、 $- \frac{2 \sqrt{2}}{3}$

查看试题解析
9. 已知 $\tan α = \frac{2 \cos α}{5 + \sin α}$ ，则 $\cos (\frac{3 π}{2} - α) =$ （）

A、 $\frac{1}{3}$ B、 $- \frac{2 \sqrt{2}}{3}$ C、 $- \frac{1}{3}$ D、 $\frac{2 \sqrt{2}}{3}$

查看试题解析
10. 若 $\sin (\frac{π}{4} - α) = \frac{2}{3}$ ，则 $\sin 2 α =$ （）

A、 $\frac{1}{9}$ B、 $\frac{4}{9}$ C、 $\frac{5}{9}$ D、 $\frac{8}{9}$

查看试题解析
11. $\cos (- 600 °) =$ （）

A、 $\frac{\sqrt{3}}{2}$ B、 $- \frac{\sqrt{3}}{2}$ C、 $\frac{1}{2}$ D、 $- \frac{1}{2}$

查看试题解析
12. 已知角 $θ \in (\frac{π}{2} ， π)$ ，角 $α \in (0 ， 2 π)$ ， $α$ 终边上有一点 $(- s i n θ ， c o s θ)$ ，则 $α =$ （）

A、 $θ + \frac{π}{2}$ B、 $θ + \frac{3 π}{2}$ C、 $\frac{π}{4}$ D、 $\frac{5 π}{4}$

查看试题解析

二、填空题

13. 若点 $P (\cos θ, \sin θ)$ 与点 $Q (\cos (θ + \frac{π}{6}), \sin (θ + \frac{π}{6}))$ 关于 $y$ 轴对称，写出一个符合题意的 $θ =$ ．

查看试题解析
14. 以俄国著名数学家切比雪夫（Tschebyscheff，1821-1894）的名字命名的第一类切比雪夫多项式 $T_{n} (x)$ 和第二类切比雪夫多项式 $U_{n} (x)$ ，起源于多倍角的余弦函数和正弦函数的展开式，是与棣莫弗定理有关、以递归方式定义的多项式序列，是计算数学中的特殊函数． $T_{n} (x)$ 有许多良好的结论，例如：① $T_{1} (x) = x$ ， $T_{2} (x) = 2 x^{2} - 1$ ，对于正整数 $n \geq 3$ 时，有 $T_{n} (x) = 2 x \cdot T_{n - 1} (x) - T_{n - 2} (x)$ 成立，② $\forall θ \in R$ ， $T_{n} (c o s θ) = c o s n θ$ 成立．由上述结论可得 $T_{4} (c o s 18 °)$ 的数值为．

查看试题解析
15. 已知函数 $f (x) = s i n (c o s x) + c o s x$ ，现有以下说法：
①直线 $x = π$ 是 $f (x)$ 图象的一条对称轴；
② $f (x)$ 在 $[π ， 2 π]$ 单调递增；
③ $\exists x \in R$ ， $f (x) \geq 1 + \frac{\sqrt{6} + \sqrt{2}}{4}$ .
则上述说法正确的序号是.

查看试题解析
16. 已知 $s i n (α + \frac{π}{2}) = - \frac{1}{3}$ ， $α \in [0 ， π]$ ，则 $t a n α =$ .

查看试题解析
17. 已知 $t a n (θ + \frac{5 π}{4}) = - 2$ ，则tanθ=.

查看试题解析
18. 已知 $α$ 为锐角，若 $s i n (α + \frac{3 π}{2}) = - \frac{1}{3}$ ，则 $c o s (α - \frac{π}{4}) =$ ．

查看试题解析
19. 若 $s i n α = \frac{3}{5}$ ， $α \in (\frac{π}{2} ， π)$ ，则 $t a n α =$ .

查看试题解析
20. 在平面直角坐标系中，角 $α$ 的顶点在坐标原点，始边在x轴的非负半轴，终边过点 $(- 2 ， y)$ 且 $t a n (π - α) = 2$ ，则 $s i n α =$ ．

查看试题解析
21. 已知 $c o s \frac{π}{12} c o s x + s i n \frac{π}{12} s i n \frac{7 π}{6} = \frac{\sqrt{2}}{2}$ ，请写出一个满足条件的 $x =$ ．

查看试题解析
22. $\cos (α - \frac{π}{4}) = \frac{\sqrt{2}}{4}$ ，则 $\sin 2 α$ 的值为．

查看试题解析
23. 已知 $α$ ， $β$ 均为锐角，若 $\cos (α + β) = 0$ ， $\tan β = \frac{1}{3}$ ，则 $\cos α =$ ．

查看试题解析

三、解答题

24. △ABC的内角A，B，C的对边分别为a，b，c，已知 $\cos^{2} (\frac{π}{2} + A) + \cos A = \frac{5}{4}$ ．

(1)、求A；

(2)、若 $b - c = \frac{\sqrt{3}}{3} a$ ，证明：△ABC是直角三角形．

查看试题解析
25. 在① $a c = \sqrt{3}$ ，② $c sin A = 3$ ，③ $c = \sqrt{3} b$ 这三个条件中任选一个，补充在下面问题中，若问题中的三角形存在，求 $c$ 的值；若问题中的三角形不存在，说明理由．
问题：是否存在 $△ A B C$ ，它的内角 $A, B, C$ 的对边分别为 $a, b, c$ ，且 $sin A = \sqrt{3} sin B$ ， $C = \frac{π}{6}$ ， ▲ ?

注：如果选择多个条件分别解答，按第一个解答计分．

查看试题解析
26. 设函数 $f (x) = s i n x - c o s x$ $(x \in R)$ .

(1)、求函数 $y = f (x) \cdot f (- x)$ 的最小正周期及其对称中心；

(2)、求函数 $y = [f (x)]^{2} + {[f (x + \frac{π}{4})]}^{2}$ 在 $[- \frac{π}{4} ， \frac{π}{4}]$ 上的值域.

查看试题解析
27. 如图，在 $△ A B C$ 中，D是AC边上一点， $∠ A B C$ 为钝角， $∠ D B C = 90 °$ ．

(1)、证明： $c o s ∠ A D B + s i n C = 0$ ；

(2)、若 $A B = 2 \sqrt{7}$ ， $B C = 2$ ，再从下面①②中选取一个作为条件，求 $△ A B D$ 的面积．
① $s i n ∠ A B C = \frac{3 \sqrt{21}}{14}$ ； ② $A C = 3 A D$ ．
注：若选择两个条件分别解答，则按第一个解答计分．

查看试题解析
28. 在 $△ A B C$ 中，角A，B，C的对边分别为a，b，c.已知 $b = 2$ ， $c s i n \frac{B + C}{2} = a s i n C$

(1)、求角A的大小；

(2)、请在① $s i n B = \frac{\sqrt{21}}{7}$ ② $a + c = 7$ 两个条件任选一个，求 $△ A B C$ 的面积.（如果分别选择多个条件进行解答.按第一个解答过程计分）

查看试题解析
29. 在△ABC中，a，b，c分别为角A，B，C的对边，已知 $\sqrt{3} b s i n (\frac{π}{2} + A) = a s i n B$ ．

(1)、求角A的大小；

(2)、若b，a，c成等比数列，判断△ABC的形状．

查看试题解析
30. 在 $△ A B C$ 中，角A，B，C所对的边分别为a，b，c，其中 $c = 4$ ，且满足 $a c o s C = c s i n A$ ．

(1)、求角C的大小；

(2)、若 $2 s i n (B + \frac{π}{4}) = c - 2 \sqrt{3} c o s A$ ，求 $△ A B C$ 的面积．

查看试题解析
31. 在 $△ A B C$ 中，内角A，B，C所对的边分别为a，b，c，已知 $\sqrt{3} b s i n \frac{B + C}{2} = a s i n B$ ．

(1)、求A；

(2)、若D为 $A C$ 的中点，E为 $∠ B A C$ 的平分线与 $B C$ 的交点，且 $B D = A C$ ，求 $\frac{C E}{B E}$ 的值．

查看试题解析
32. 在 $△ A B C$ 中，内角 $A$ ， $B$ ， $C$ 所对的边分别为 $a$ ， $b$ ， $c$ ， $s i n B = s i n \frac{A + C}{2}$ .

(1)、求 $B$ ；

(2)、若 $s i n A = 2 s i n B - s i n C$ ， $△ A B C$ 面积为 $\frac{\sqrt{3}}{4}$ ，求 $△ A B C$ 的周长．

查看试题解析
33. 如图，在平面四边形 $A B C D$ 中，对角线 $A C$ 平分 $∠ B A D$ ， $△ A B C$ 的内角A，B，C的对边分别为a，b，c，已知 $\sqrt{2} b c o s B + a c o s C + c c o s A = 0$

(1)、求B；

(2)、若 $A B = C D = 2$ ， $△ A B C$ 的面积为2，求 $A D$

查看试题解析
34. 在 $△ A B C$ 中，角A，B，C对应的边分别是a，b，c．已知 $c o s 2 B = 3 c o s (A + C) + 1$ ．

(1)、求B；

(2)、若 $△ A B C$ 的面积 $S = 5 \sqrt{3} ， a = 10$ ，求 $s i n A s i n C$ 的值．

查看试题解析
35. 在 $△ A B C$ 中，a，b，c分别为角A，B，C所对的边，已知 $c^{2} = a^{2} - b^{2} + \sqrt{3} b c$ ， $c o s A = 3 - \frac{a c o s B}{b}$ ．

(1)、求角A及 $\frac{c}{b}$ 的值；

(2)、若D为AB边上一点，且 $C D ⊥ A C$ ， $C D = 2$ ，求 $△ B C D$ 的面积．

查看试题解析