【备考2024】高考数学(三角函数版块)细点逐一突破训练:同角三角函数间的基本关系3
试卷更新日期:2023-08-18 类型:二轮复习
一、选择题
-
1. 在△ABC中,cosC= ,AC=4,BC=3,则tanB=( )A、 B、2 C、4 D、82. 已知 ,且 ,则 ( )A、 B、 C、 D、3. 若 , , 则( )A、 B、 C、 D、4. 已知 , 则( )A、 B、 C、 D、5. 若为第二象限角,且 , 则=( )A、 B、 C、 D、6. 已知 , 则( )A、2 B、 C、 D、7. 已知 , 则( )A、 B、 C、 D、8. 已知 , 则( )A、 B、 C、 D、9. 已知 , , 则( )A、 B、 C、 D、10. 已知角的始边与轴非负半轴重合,终边上一点 , 若 , 则( )A、3 B、 C、 D、11. 已知 , , 则( )A、 B、 C、 D、12. 若 ,则 等于( )A、 B、2 C、-1 D、
二、填空题
-
13. 已知tanθ=2,则cos2θ=;tan(θ﹣ )= .14. 如图,四边形中,且 , 则四边形面积取最大值时,.
 15. 已知函数 ,给出下列四个命题:① 的图象关于 轴对称;②8为 的一个周期;③当 时, ;④ 在 上单调递增.其中真命题有(填序号).16. 在中, , D是线段上一点,且 , 则 , 的长为 .17. 已知 , , 则.18. 已知为锐角,且 , 则的值为 .19. 如图,在 中, , , ,点 是边 (端点除外)上的一动点.若将 沿直线 翻折,能使点 在平面 内的射影 落在 的内部(不包含边界),且 .设 ,则t的取值范围是.
15. 已知函数 ,给出下列四个命题:① 的图象关于 轴对称;②8为 的一个周期;③当 时, ;④ 在 上单调递增.其中真命题有(填序号).16. 在中, , D是线段上一点,且 , 则 , 的长为 .17. 已知 , , 则.18. 已知为锐角,且 , 则的值为 .19. 如图,在 中, , , ,点 是边 (端点除外)上的一动点.若将 沿直线 翻折,能使点 在平面 内的射影 落在 的内部(不包含边界),且 .设 ,则t的取值范围是.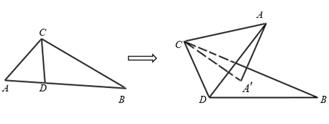 20. 已知为锐角, , 则.21. 在中,角A,B,C所对的边分别为a,b,c,且满足 , 则的取值范围是.22. 已知为第二象限角,若 , 则的值为 .23. 若=3,则= .
20. 已知为锐角, , 则.21. 在中,角A,B,C所对的边分别为a,b,c,且满足 , 则的取值范围是.22. 已知为第二象限角,若 , 则的值为 .23. 若=3,则= .三、解答题
-
24. △ABC的内角A,B,C的对边分别为a,b,c,已知 .(1)、求A;(2)、若 ,证明:△ABC是直角三角形.25. 在△ABC中,角A,B,C的对边分别为a,b,c,已知 .
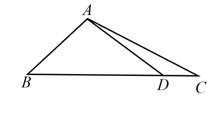 (1)、求 的值;(2)、在边BC上取一点D,使得 ,求 的值.26. 在 中, ,再从条件①、条件②这两个条件中选择一个作为已知,求:
(1)、求 的值;(2)、在边BC上取一点D,使得 ,求 的值.26. 在 中, ,再从条件①、条件②这两个条件中选择一个作为已知,求:(Ⅰ)a的值:
(Ⅱ) 和 的面积.
条件①: ;
条件②: .
注:如果选择条件①和条件②分别解答,按第一个解答计分.
27. 在中,内角A,B,C所对的边分别为a,b,c,且 . 求:(1)、;(2)、的取值范围.28. 已知为非直角三角形,.(1)、证明:;(2)、求的最小值.29. 如图,一架飞机从地飞往地,两地相距.飞行员为了避开某一区域的雷雨云层,从机场起飞以后,就沿与原来的飞行方向成角的方向飞行,飞行到地,再沿与原来的飞行方向成角的方向继续飞行到达终点. (1)、求、两地之间的距离;(2)、求.30. 在① , ② , ③三个条件中任选一个,补充到下面问题中,并解答.
(1)、求、两地之间的距离;(2)、求.30. 在① , ② , ③三个条件中任选一个,补充到下面问题中,并解答.已知锐角的内角A,B,C,的对边分别为a,b,c满足____(填写序号即可)
(1)、求B﹔(2)、若 , 求的取值范围.31. 如图,在四边形中, , , , .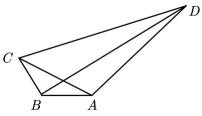 (1)、求;(2)、求 .32. 在△中,内角 , , 的对边分别为 , , , 若.(1)、求角;(2)、点在线段上,且 , , 求△的面积.33. 中,内角A,B,C所对的边分别为a,b,c,且 .(1)、求;(2)、若的外接圆半径为 , 且 , 求的面积.
(1)、求;(2)、求 .32. 在△中,内角 , , 的对边分别为 , , , 若.(1)、求角;(2)、点在线段上,且 , , 求△的面积.33. 中,内角A,B,C所对的边分别为a,b,c,且 .(1)、求;(2)、若的外接圆半径为 , 且 , 求的面积.