【备考2024】高考数学(三角函数版块)细点逐一突破训练:任意角的三角函数1
试卷更新日期:2023-08-18 类型:二轮复习
一、选择题
-
1. 如图,A,B是半径为2的圆周上的定点,P为圆周上的动点,∠APB是锐角,大小为β.图中阴影区域的面积的最大值为( )
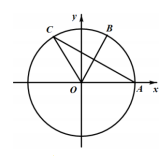
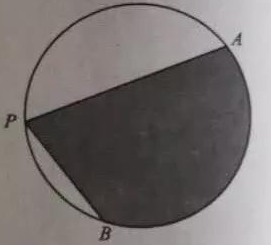 A、4β+4cosβ B、4β+4sinβ C、2β+2cosβ D、2β+2sinβ2. 已知角α的顶点为坐标原点,始边与x轴的非负半轴重合,终边上有两点A(1,a),B(2,b),且cos2α= ,则|a-b|=( )A、 B、 C、 D、13. 在平面坐标系中, , , , 是圆 上的四段弧(如图),点P在其中一段上,角 以Ox为始边,OP为终边,若 ,则P所在的圆弧是( )
A、4β+4cosβ B、4β+4sinβ C、2β+2cosβ D、2β+2sinβ2. 已知角α的顶点为坐标原点,始边与x轴的非负半轴重合,终边上有两点A(1,a),B(2,b),且cos2α= ,则|a-b|=( )A、 B、 C、 D、13. 在平面坐标系中, , , , 是圆 上的四段弧(如图),点P在其中一段上,角 以Ox为始边,OP为终边,若 ,则P所在的圆弧是( ) A、 B、 C、 D、4. 如图,正方形ABCD的边长为1,延长BA至E,使AE=1,连接EC、ED则sin∠CED=( )
A、 B、 C、 D、4. 如图,正方形ABCD的边长为1,延长BA至E,使AE=1,连接EC、ED则sin∠CED=( ) A、 B、 C、 D、5. 已知 , 则“”是“”的A、充分不必要条件 B、必要不充分条件 C、充分必要条件 D、既不充分也不必要条件6. 已知角α的顶点在原点,始边与x轴的正半轴重合,终边经过点 , 则( )A、 B、 C、 D、27. 设 , 若在区间上存在a,b且 , 使得 , 则下列所给的值中只可能是( )A、 B、 C、2 D、8. 在平面直角坐标系中,角 , 均以坐标原点为顶点,轴的正半轴为始边.若点在角的终边上,点在角的终边上,则( )A、 B、 C、 D、9. 三棱锥中,平面 , , 记 , , , 则下列正确的是( )A、 B、 C、 D、若 , 则与平面所成的角为10. 在平面直角坐标系中,若角以轴非负半轴为始边,其终边与单位圆交点的横坐标为 , 则的一个可能取值为( )A、 B、 C、 D、11. 在平面直角坐标系中,角以为始边,终边与单位圆交于点 , 则( )A、 B、 C、 D、12. 如图,( )
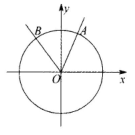
A、 B、 C、 D、5. 已知 , 则“”是“”的A、充分不必要条件 B、必要不充分条件 C、充分必要条件 D、既不充分也不必要条件6. 已知角α的顶点在原点,始边与x轴的正半轴重合,终边经过点 , 则( )A、 B、 C、 D、27. 设 , 若在区间上存在a,b且 , 使得 , 则下列所给的值中只可能是( )A、 B、 C、2 D、8. 在平面直角坐标系中,角 , 均以坐标原点为顶点,轴的正半轴为始边.若点在角的终边上,点在角的终边上,则( )A、 B、 C、 D、9. 三棱锥中,平面 , , 记 , , , 则下列正确的是( )A、 B、 C、 D、若 , 则与平面所成的角为10. 在平面直角坐标系中,若角以轴非负半轴为始边,其终边与单位圆交点的横坐标为 , 则的一个可能取值为( )A、 B、 C、 D、11. 在平面直角坐标系中,角以为始边,终边与单位圆交于点 , 则( )A、 B、 C、 D、12. 如图,( )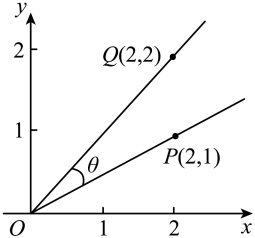 A、 B、 C、 D、13. 如图,在平面直角坐标系中,分别是单位圆上的四段弧,点在其中一段上,角以为始边,为终边.若 , 则所在的圆弧是( )
A、 B、 C、 D、13. 如图,在平面直角坐标系中,分别是单位圆上的四段弧,点在其中一段上,角以为始边,为终边.若 , 则所在的圆弧是( )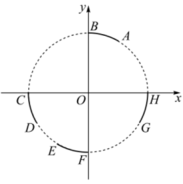 A、 B、 C、 D、14. 下图改编自李约瑟所著的《中国科学技术史》,用于说明元代数学家郭守敬在编制《授时历》时所做的天文计算.图中的 , , , 都是以O为圆心的圆弧,CMNK是为计算所做的矩形,其中M,N,K分别在线段OD,OB,OA上, , . 记 , , , , 则( )
A、 B、 C、 D、14. 下图改编自李约瑟所著的《中国科学技术史》,用于说明元代数学家郭守敬在编制《授时历》时所做的天文计算.图中的 , , , 都是以O为圆心的圆弧,CMNK是为计算所做的矩形,其中M,N,K分别在线段OD,OB,OA上, , . 记 , , , , 则( )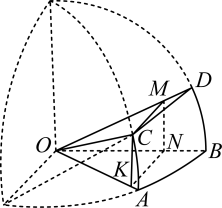 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
15. 已知点P在圆x2+y2=1上,点A的坐标为(﹣2,0),O为原点,则 • 的最大值为 .16. 在平面直角坐标系中,若角的顶点为坐标原点,始边与x轴的非负半轴重合,终边与以点O为圆心的单位圆交于点 , 则的值为.17. 已知函数的图象在处的切线的倾斜角为α,则 .18. 在平面直角坐标系中,点绕着原点顺时针旋转 得到点 , 点的横坐标为.19. 在平面直角坐标系中,角的终边经过点 , 则 .20. 某游乐场中的摩天轮作匀速圆周运动,其中心距地面20.5米,半径为20米.假设从小军同学在最低点处登上摩天轮开始计时,第6分钟第一次到达最高点.则第10分钟小军同学离地面的高度为米.
 21. 如图所示,角的终边与单位圆交于点 , 已知点的坐标为 , 则 .
21. 如图所示,角的终边与单位圆交于点 , 已知点的坐标为 , 则 .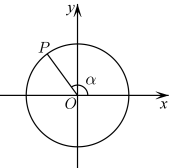 22. 已知角θ的终边过点 ,且 ,则tanθ= .23. 在平面直角坐标系xOy中,圆O与x轴的正半轴交于点A,点B,C在圆O上,若射线OB平分∠AOC,B( , ),则点C的横坐标为.24. 某中学开展劳动实习,学生需测量某零件中圆弧的半径.如图,将三个半径为的小球放在圆弧上,使它们与圆弧都相切,左、右两个小球与中间小球相切.利用“十”字尺测得小球的高度差为 , 则圆弧的半径为.
22. 已知角θ的终边过点 ,且 ,则tanθ= .23. 在平面直角坐标系xOy中,圆O与x轴的正半轴交于点A,点B,C在圆O上,若射线OB平分∠AOC,B( , ),则点C的横坐标为.24. 某中学开展劳动实习,学生需测量某零件中圆弧的半径.如图,将三个半径为的小球放在圆弧上,使它们与圆弧都相切,左、右两个小球与中间小球相切.利用“十”字尺测得小球的高度差为 , 则圆弧的半径为. 25. 如图,已知扇形的半径为 , 以为原点建立平面直角坐标系, , , 则的中点的坐标为.
25. 如图,已知扇形的半径为 , 以为原点建立平面直角坐标系, , , 则的中点的坐标为.
三、解答题
-
26. 在平面直角坐标系 中, 在以原点 为圆心半径等1的圆上,将射线 绕原点 逆时针方向旋转 后交该圆于点 ,设点 的横坐标为 ,纵坐标 .
 (1)、如果 , ,求 的值(用 表示);(2)、如果 ,求 的值.27. 已知角的顶点与原点O重合,它的始边与x轴的非负半轴重合,终边过点.(1)、求的值;(2)、求值:.28. 在极坐标系中,O为极点,直线与以点为圆心,且过点的圆相交于A,B两点.(1)、求圆C的极坐标方程;(2)、若 , 求 .29. 在极坐标系中,射线与以为圆心,为半径的圆相交于两点.(1)、求圆的极坐标方程;(2)、若 , 求 .30. 在平面直角坐标系 中,已知角a的顶点在坐标原点,始边与x轴的非负半轴重合,终边经过一点 .(1)、若 ,求 的值;(2)、若 且 ,求 的单调增区间.31. 在直角坐标系 xOy 中,以坐标原点为极点, x 轴正半轴为极轴建立极坐标系,曲线 C 的参数方程为 (θ为参数),直线 l 经过点 且倾斜角为 α .
(1)、如果 , ,求 的值(用 表示);(2)、如果 ,求 的值.27. 已知角的顶点与原点O重合,它的始边与x轴的非负半轴重合,终边过点.(1)、求的值;(2)、求值:.28. 在极坐标系中,O为极点,直线与以点为圆心,且过点的圆相交于A,B两点.(1)、求圆C的极坐标方程;(2)、若 , 求 .29. 在极坐标系中,射线与以为圆心,为半径的圆相交于两点.(1)、求圆的极坐标方程;(2)、若 , 求 .30. 在平面直角坐标系 中,已知角a的顶点在坐标原点,始边与x轴的非负半轴重合,终边经过一点 .(1)、若 ,求 的值;(2)、若 且 ,求 的单调增区间.31. 在直角坐标系 xOy 中,以坐标原点为极点, x 轴正半轴为极轴建立极坐标系,曲线 C 的参数方程为 (θ为参数),直线 l 经过点 且倾斜角为 α .
(1)、求曲线 C 的极坐标方程和直线 的参数方程;
(2)、已知直线 l 与曲线 C 交于 A, B,满足 A 为 MB 的中点,求 tanα .
32. 已知角 的顶点与原点 重合,始边与 轴的非负半轴重合,它的终边经过单位圆上一点 .(1)、求 的值;(2)、若角 满足 ,求 的值.