甘肃省白银市2022-2023学年七年级下学期数学期末考试试卷
试卷更新日期:2023-08-18 类型:期末考试
一、单选题
-
1. 在一些汉字的美术字中,有一些是轴对称图形,下面四个美术字中,可以近似地看作是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 计算的结果是( )A、 B、 C、5 D、3. 如图,在中,为边上的中线,若 , 则( )
2. 计算的结果是( )A、 B、 C、5 D、3. 如图,在中,为边上的中线,若 , 则( ) A、2 B、3 C、4 D、54. 用直尺和圆规作一个角的平分线的示意图如图所示,则能说明∠AOC=∠BOC的依据是( )
A、2 B、3 C、4 D、54. 用直尺和圆规作一个角的平分线的示意图如图所示,则能说明∠AOC=∠BOC的依据是( )
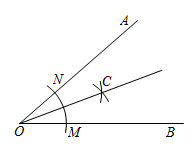 A、SSS B、ASA C、AAS D、SAS5. 将2个红球、3个白球放入一个不透明的袋子里,从中摸出4个球,恰好红球、白球都摸到,这件事情( )A、可能发生 B、不可能发生 C、必然发生 D、无法确定6. 如图,若 , 则的度数是( )
A、SSS B、ASA C、AAS D、SAS5. 将2个红球、3个白球放入一个不透明的袋子里,从中摸出4个球,恰好红球、白球都摸到,这件事情( )A、可能发生 B、不可能发生 C、必然发生 D、无法确定6. 如图,若 , 则的度数是( ) A、 B、 C、 D、7. 如图,已知 , , 那么要得到 , 还应给出的条件是( )
A、 B、 C、 D、7. 如图,已知 , , 那么要得到 , 还应给出的条件是( ) A、 B、 C、 D、8. 周末,小明在黄河湿地公园匀速骑行游玩,沿直线骑行前进了800米,停车欣赏了一下迷人的风景,又原路返回了600米,再前进了1000米,在这个过程中,他离起点的距离s与时间t的关系示意图是( )A、
A、 B、 C、 D、8. 周末,小明在黄河湿地公园匀速骑行游玩,沿直线骑行前进了800米,停车欣赏了一下迷人的风景,又原路返回了600米,再前进了1000米,在这个过程中,他离起点的距离s与时间t的关系示意图是( )A、 B、
B、 C、
C、 D、
D、 9. 若是一个二项式的平方,则m的值为( )A、 B、10 C、4或 D、或1010. 如图,直线 , 的顶点B , C分别在上,若 , 则的度数是( )
9. 若是一个二项式的平方,则m的值为( )A、 B、10 C、4或 D、或1010. 如图,直线 , 的顶点B , C分别在上,若 , 则的度数是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 环境空气质量问题已经成为人们日常生活所关心的重要问题,我国新修订的《环境空气质量标准》中增加了 检测指标,“ ”是指大气中危害健康的直径小于或等于2.5微米的颗粒物,2.5微米即0.0000025米.用科学记数法表示0.0000025为.12. 计算: .13. 等边三角形是轴对称图形,它的对称轴共有 条.14. 已知 , , , 则的度数为 .15. 某人购进一批大庙香水梨到市场上零售,已知卖出香水梨的质量x与售价y的关系如下表:
质量x/kg
1
2
3
4
5
售价y/元
20
40
60
80
100
写出用x表示y的关系式: .
16. 如图,已知ab,∠1=65°,则∠2的度数为 . 17. 如图,是小鹏自己创作的正方形飞镖盘,并在盒内画了两个小正方形,则小鹏在投掷飞镖时,飞镖扎在阴影部分的概率
17. 如图,是小鹏自己创作的正方形飞镖盘,并在盒内画了两个小正方形,则小鹏在投掷飞镖时,飞镖扎在阴影部分的概率 18. 如图,第1个图中有1个三角形,第2个图中共有5个三角形,第3个图中共有9个三角形,…,依此类推,则第2023个图中共有个三角形.
18. 如图,第1个图中有1个三角形,第2个图中共有5个三角形,第3个图中共有9个三角形,…,依此类推,则第2023个图中共有个三角形.
三、解答题
-
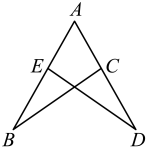
19. 计算: .20. 如图, , , 与全等吗?为什么?
 21. 先化简,再求值: , 其中 .22. 如图,这是一个由4条线段构成的“鱼”形图案,其中 , , , 找出图中的平行线,并说明理由.
21. 先化简,再求值: , 其中 .22. 如图,这是一个由4条线段构成的“鱼”形图案,其中 , , , 找出图中的平行线,并说明理由. 23. 如图,在中是的垂直平分线, , 的周长为 , 求的周长.
23. 如图,在中是的垂直平分线, , 的周长为 , 求的周长. 24. 如图,已知线段a和 , 利用尺规作 , 使得 , , .
24. 如图,已知线段a和 , 利用尺规作 , 使得 , , . 25. 如图,在一个边长为的正方形的四个角上,都剪去一个大小相同的小正方形,当小正方形的边长由小到大变化时,图中阴影部分的面积也随之发生变化.
25. 如图,在一个边长为的正方形的四个角上,都剪去一个大小相同的小正方形,当小正方形的边长由小到大变化时,图中阴影部分的面积也随之发生变化. (1)、在这个变化过程中,自变量、因变量各是什么?(2)、若小正方形的边长为 , 图中阴影部分的面积为 , 请直接写出y与x之间的关系式;并求出当时,图中阴影部分的面积.26. 小明和小强都想参加学校社团组织的暑假实践活动,但只有一个名额,小明提议用如下的办法决定谁去参加活动:将一个转盘9等分,分别标上1至9九个数字,随意转动一次转盘,若转到奇数,小明去参加活动;若转到偶数,小强去参加活动.
(1)、在这个变化过程中,自变量、因变量各是什么?(2)、若小正方形的边长为 , 图中阴影部分的面积为 , 请直接写出y与x之间的关系式;并求出当时,图中阴影部分的面积.26. 小明和小强都想参加学校社团组织的暑假实践活动,但只有一个名额,小明提议用如下的办法决定谁去参加活动:将一个转盘9等分,分别标上1至9九个数字,随意转动一次转盘,若转到奇数,小明去参加活动;若转到偶数,小强去参加活动. (1)、转盘转到奇数的概率是多少?(2)、你认为这个游戏公平吗?请说明理由.27. 如图,在中,D , E分别是 , 上任意一点,连接 , 若 , .
(1)、转盘转到奇数的概率是多少?(2)、你认为这个游戏公平吗?请说明理由.27. 如图,在中,D , E分别是 , 上任意一点,连接 , 若 , . (1)、求线段的取值范围;(2)、若 , , , 求的度数.28. 如图,在等边中, , 现有M、N两点分别从点A、点B同时出发,沿三角形的边按顺时针方向运动,已知点M的速度为 , 点N的速度为 . 当点N第一次到达点B时,M、N两点同时停止运动.
(1)、求线段的取值范围;(2)、若 , , , 求的度数.28. 如图,在等边中, , 现有M、N两点分别从点A、点B同时出发,沿三角形的边按顺时针方向运动,已知点M的速度为 , 点N的速度为 . 当点N第一次到达点B时,M、N两点同时停止运动.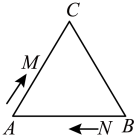 (1)、点M、N运动几秒后,M、N两点重合?(2)、点M、N运动几秒后,可得到等边?(提示:有一个角是的等腰三角形是等边三角形)(3)、当点M、N在边上运动时,是否存在以为底边的等腰?若存在,请求出此时点M、N运动的时间;若不存在,请说明理由.
(1)、点M、N运动几秒后,M、N两点重合?(2)、点M、N运动几秒后,可得到等边?(提示:有一个角是的等腰三角形是等边三角形)(3)、当点M、N在边上运动时,是否存在以为底边的等腰?若存在,请求出此时点M、N运动的时间;若不存在,请说明理由.