贵州省黔东南州2022-2023学年七年级下学期数学期末考试试卷

试卷更新日期：2023-08-18 类型：期末考试

进入出卷网下载

一、单选题

1. $\sqrt{4}$ 的值为（）

A、2 B、 $- 2$ C、 $\pm 2$ D、 $- 4$

查看试题解析
2. 已知坐标平面内点A的坐标为 $（ - 2 ， 6 ）$ ，则点A在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
3. 下列方程组是二元一次方程组的是（）

A、 ${\begin{array}{l} m n = 2 \\ m + n = 3 \end{array}$ B、 ${\begin{array}{l} 5 m - 2 n = 0 \\ \frac{1}{m} + n = 3 \end{array}$ C、 ${\begin{array}{l} m + n = 0 \\ 3 m + 2 a = \frac{1}{6} \end{array}$ D、 ${\begin{array}{l} m = 8 \\ \frac{m}{3} - \frac{n}{2} = 1 \end{array}$

查看试题解析
4. 下列调查中，适宜采用全面调查（普查）方式的是（）

A、对一批灯泡使用寿命的调查 B、对一枚用于发射卫星的运载火箭各零部件的检查 C、对某品牌烟花爆竹燃放安全的调查 D、对全国九年级学生身高现状的调查

查看试题解析
5. 在数轴上表示不等式组 ${\begin{array}{l} x < 2 \\ x > 1 \end{array}$ 的解集，其中正确的是（）

A、 B、 C、 D、

查看试题解析
6. 下列说法，①同位角相等；②经过一点，有且只有一条直线与已知直线平行；③垂直于同一条直线的两条直线互相平行；④两条直线被第三条直线所截，同旁内角的平分线互相垂直；其中正确的是（）

A、0个 B、1个 C、2个 D、3个

查看试题解析
7. 如图，下列条件中能判定直线l₁//l₂的是（）

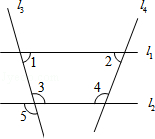A、∠1=∠2 B、∠1=∠5 C、∠1+∠3=180° D、∠3=∠5

查看试题解析
8. 下列式子正确的是（）

A、 $\sqrt{9} = \pm 3$ B、 $\sqrt{16} = 8$ C、 $\sqrt{{(- 2)}^{2}} = - 2$ D、 $- \sqrt[3]{8} = - 2$

查看试题解析
9. 已知直线 $M N$ 平行于 $x$ 轴，若点M的坐标为 $(- 1 ， 3)$ ，且点N到y轴的距离等于4，则点N的坐标是（）

A、 $(- 1 ， 4)$ 或 $(- 1 ， - 4)$ B、 $(4 ， 3)$ 或 $(- 4 ， - 3)$ C、 $(- 1 ， 4)$ 或 $(1 ， - 4)$ D、 $(4 ， 3)$ 或 $(- 4 ， 3)$

查看试题解析
10. 已知 $\sqrt{5.21} \approx 2.28$ ， $\sqrt{52.1} \approx 7.22$ ，则 $\sqrt{0.0521}$ 的值约为（）

A、 $0.228$ B、 $0.0722$ C、 $0.0228$ D、 $0.722$

查看试题解析
11. 已知关于 $x$ 的不等式 $3 x - a > 1$ 有且只有1个负整数解，则 $a$ 的取值范围是（）

A、 $a$ ＞4 B、 $- 7 \leq a < - 4$ C、 $- 7 < a \leq - 4$ D、 $a \leq 4$

查看试题解析
12. 打折前，买60件A商品和30件B商品用了1080元，买50件A商品和10件B商品用了840元打折后，买500件A商品和500件B商品用了9600元，比不打折少花（）

A、300元 B、400元 C、500元 D、600元

查看试题解析

二、填空题

13. 电影院里5排2号的座位记为 $(5 ， 2)$ ，则 $(3 ， 4)$ 表示．

查看试题解析
14. 将实数 $- π$ ， $0$ ， $- \sqrt{3}$ ， $2$ 由小到大用“ $<$ ”号连起来，可表示为．

查看试题解析
15. 如图，已知直线 $A B ∥ C D$ ，直线 $M N$ 分别交 $A B$ 、 $C D$ 于点 $O$ 、 $P$ ，过点 $O$ 作 $O E ⊥ M N$ ，垂足为点 $O$ ，若 $∠ B O E = 58 °$ ，则 $∠ D P N =$ ．

查看试题解析
16. 如图，平面直角坐标系中有两点 $A (0 ， 3)$ 和 $B (4 ， 0)$ ， $A B = 5$ ， M为 $A B$ 上一动点，连接 $O M$ ，则 $O M$ 的最小值为．

查看试题解析

三、解答题

17. 计算：

(1)、 $\sqrt{3} (\sqrt{3} + 1) - 2 \sqrt{3}$ ；

(2)、 ${(- 1)}^{2} + \sqrt{{(- 2)}^{2}} - \sqrt[3]{8} + | 1 - \sqrt{2} |$ ．

查看试题解析
18.

(1)、解方程组 ${\begin{array}{l} 2 m - n = 4 \\ 3 m + 2 n = - 1 \end{array}$ ；

(2)、解不等式组 ${\begin{array}{l} 3 (x - 1) > 5 x + 1 \\ \frac{x - 5}{4} \leq 1 - \frac{1}{2} x \end{array}$ ，并把它的解集表示在数轴上．

查看试题解析
19. 如图，已知 $△ A B C$ 中，点 $A (- 2 ， 1) ， B (- 3 ， - 2) ， C (1 ， - 2)$ ，平移 $△ A B C$ ，使得点A平移到点 $A_{1} （ 2 ， 4 ）$ 的位置，得到 $△ A_{1} B_{1} C_{1}$ ．

(1)、在图中画出 $△ A_{1} B_{1} C_{1}$ ；

(2)、写出点 $B_{1} ， C_{1}$ 的坐标；

(3)、在y轴上有一点P ，且 $△ B C P$ 与 $△ A B C$ 面积相等，请直接写出点P的坐标．

查看试题解析
20. 某校七年级学生参加60秒跳绳测试，从七年级学生中随机抽取了部分同学的成绩，并绘制了如下不完整的统计表和统计图，请解答下列问题：
次数分组
频数
百分比
$60 \leq x < 80$
3
$6 %$
$80 \leq x < 100$
4
$8 %$
$100 \leq x < 120$
19
$38 %$
$120 \leq x \leq 140$
m
$20 %$
$140 \leq x \leq 160$
8
$160 \leq x \leq 180$
n
$180 \leq x \leq 200$
2
$4 %$
合计
$100 %$

(1)、 $m =$ ， $n =$ ；

(2)、请补全频数分布直方图；

(3)、若该校七年级有300名学生，请估计60秒能跳120次及以上的学生有多少人？

查看试题解析
21. 完成下面推理过程：如图，已知 $D E ∥ B C$ ， $D F 、 B E$ 分别平分 $∠ A D E 、 ∠ A B C$ ，请写出可推得 $∠ F D E = ∠ D E B$ 的理由：
∵ $D E ∥ B C$ （已知），
∴ $∠ A D E =$     ▲ （               ），
∵ $D F 、 B E$ 分别平分 $∠ A D E 、 ∠ A B C$ ，
∴ $∠ A D F = \frac{1}{2}$     ▲ ， $∠ A B E = \frac{1}{2}$     ▲ ，（）
∴ $∠ A D F = ∠ A B E$ ，
∴    ▲ $∥$     ▲ （                   ）
∴ $∠ F D E = ∠ D E B$ ．（                    ）．

查看试题解析
22. 已知：如图AB∥CD ， EF交AB于G ，交CD于F ， FH平分∠EFD ，交AB于H ， ∠AGE＝50°，求：∠BHF的度数．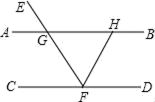

查看试题解析
23. 学校组织学生参加“防溺水”安全知识竞赛，并为这次竞赛获奖的学生准备了羽毛球拍和乒乓球拍两种奖品（每副羽毛球拍的价格相同，每副乒乓球拍的价格相同），已知购买 $1$ 副羽毛球拍和 $1$ 副乒乓球拍共需 $159$ 元；每副羽毛球拍的价格是每副乒乓球拍价格的 $2$ 倍少 $9$ 元．

(1)、每副羽毛球拍和每副乒乓球拍的价格各是多少元？

(2)、根据学校实际情况，需一次性购买羽毛球拍和乒乓球拍共 $20$ 副，但要求购买羽毛球拍和乒乓球拍的总费用不超过 $1550$ 元，学校最多可以购买多少副羽毛球拍？

查看试题解析
24. 如图，已知直线 $E F ∥ M N$ ，直线 $G H$ 分别与 $E F ， M N$ 交于C ， D两点. 点A ， B分别在直线 $E F ， M N$ 上，且与点C ， D不重合，点P是直线 $G H$ 上的动点．
　　

(1)、【问题解决】写出图1中一对相等的角；

(2)、【问题探究】如图1，若点P是线段 $C D$ 上的动点，试探究 $∠ A P B ， ∠ P A C$ ， $∠ P B D$ 之间的关系，并说明理由；

(3)、【拓展延伸】如图2，若点P在线段 $C D$ 的延长线上时，探究 $∠ A P B ， ∠ P A C$ ， $∠ P B D$ 之间的关系，并说明理由．

查看试题解析

次数分组	频数	百分比
$60 \leq x < 80$	3	$6 %$
$80 \leq x < 100$	4	$8 %$
$100 \leq x < 120$	19	$38 %$
$120 \leq x \leq 140$	m	$20 %$
$140 \leq x \leq 160$	8
$160 \leq x \leq 180$		n
$180 \leq x \leq 200$	2	$4 %$
合计		$100 %$