贵州省毕节市七星关区2022-2023学年七年级下学期数学期末考试试卷

试卷更新日期：2023-08-18 类型：期末考试

进入出卷网下载

一、单选题

1. 计算2^－2的结果是

A、 $\frac{1}{4}$ B、－ $\frac{1}{4}$ C、4 D、－4

查看试题解析
2. 一本笔记本5元，买 $x$ 本共付 $y$ 元，则5和 $x$ 分别是（）

A、常量，常量 B、变量，变量 C、常量，变量 D、变量，常量

查看试题解析
3. 下列各图中，∠1 与∠2 是对顶角的是（）

A、 B、 C、 D、

查看试题解析
4. 绿化做得好，染污就减少；垃圾分类放，环境有保障，在以下绿色食品､回收､节能､节水四个标志中，轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
5. 已知 $∠ A = 76 °$ ，则 $∠ A$ 的余角是（　　）

A、 $104 °$ B、 $124 °$ C、 $14 °$ D、 $24 °$

查看试题解析
6. 一个氧原子的质量是0.000 000 000 000 000 000 000 000 02657kg，把它用科学记数法表示是（）

A、26.57×10^-25 B、26.57×10^-27 C、2.657×10^-26 D、2.657×10^-27

查看试题解析
7. 下列长度的三条线段能组成三角形的是（　　）

A、3cm ， 5cm ， 7cm B、3cm ， 3cm ， 7cm C、4cm ， 4cm ， 8cm D、4cm ， 5cm ， 9cm

查看试题解析
8. 下列运算正确的是（　　）

A、 $a \cdot a = 2 a$ B、 ${(2 a b)}^{2} = 2 a^{2} b^{2}$ C、 $a + a = 2 a$ D、 ${(a^{2})}^{3} = a^{5}$

查看试题解析
9. 如图， $A B / / C D ， E C$ 平分 $∠ A E F$ ，若 $∠ E F D = 130 °$ ，则 $∠ E C F$ 的度数是（）

A、 $50 °$ B、 $55 °$ C、 $60 °$ D、 $65 °$

查看试题解析
10. 如图，点D在BC上，AB＝AD，∠B＝∠ADE，则补充下列条件，不一定能使△ABC≌△ADE的是（）

A、AC＝AE B、BC＝DE C、∠BAD＝∠CAE D、∠CDE＝∠CAE

查看试题解析
11. 已知 $x + y = 5$ 且 $x y = 6$ ，则 ${(x - y)}^{2}$ 的值是（　　）

A、25 B、12 C、5 D、1

查看试题解析
12. 如图所示， $△$ ABC中，AB=AC，∠A=36°，D是AC上一点，且BD=BC，过点D分别作DE⊥AB，DF⊥BC，垂足分别是E，F，下列结论：①DE=DF；②D是AC的中点；③E是AB的中点；④AB=BC+CD．其中正确的个数为（）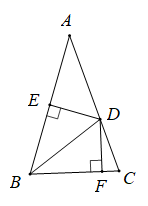

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

13. 用抽签的办法从 A 、B 、C 、D 四人中任选一人去打扫公共场地，选中 A 的概率是．

查看试题解析
14. 一个三角形的两边长分别为3和8，且第三边长为奇数，则这个三角形的周长是．

查看试题解析
15. $若 x^{2} - k x + 9$ 是一个完全平方式，则 $k =$ ．

查看试题解析
16. 在一次实验中，小强把一根弹簧的上端固定，在其下端悬挂物体，下面是测得的弹簧的长度y与所挂物体的重量x的一组对应值：在弹簧允许范围内，写出弹簧长 $y c m$ 与所挂重物 $x k g$ 的关系式．
所挂物重量 $x (k g)$
0
1
2
3
4
5
弹簧长度 $y (c m)$
20
22
24
26
28
30

查看试题解析

三、解答题

17. 计算：

(1)、 $(- 2 x^{5} + 3 x^{3} - \frac{1}{2} x^{2}) \div {(- \frac{1}{2} x)}^{2}$

(2)、 ${(3 a - b)}^{2} {(3 a + b)}^{2}$

查看试题解析
18. 先化简，再求值： $x (x + 2 y) - {(x + 1)}^{2} + 2 x$ ，其中 $x = \frac{1}{25}$ ， $y = - 25$ .

查看试题解析
19. 在一个口袋中装有4个红球和8个白球，它们除颜色外完全相同．

(1)、判断事件“从口袋中随机摸出一个球是黑球”是什么事件，并写出其发生的概率；

(2)、求从口袋中随机摸出一个球是红球的概率；；

(3)、现从口袋中取走若干个白球，并放入相同数量的红球，充分摇匀后，要使从中随机摸出一个球是红球的概率是 $\frac{5}{6}$ ，问取走了多少个白球？

查看试题解析
20. 如图，点D在 $△ A B C$ 的BC边上， $A C ∥ B E$ ， $B C = B E$ ， $∠ A B C = ∠ E$ .

(1)、求证： $△ A B C ≌ △ D E B$ ；

(2)、若 $B E = 9$ ， $A C = 4$ ，求CD的长，

查看试题解析
21. 如图：在正方形网格上有一个△ABC ．

(1)、作△ABC关于直线MN的对称图形△A'B'C′（不写作法）．

(2)、若网格上的最小正方形的边长为1，求△ABC的面积．

查看试题解析
22. 某中学的小明同学和朱老师一起从相同地点向同一方向跑步锻炼身体，朱老师先跑．当小明出发时，朱老师已经距起点200米了．他们距起点的距离s（米）与小明出发的时间t（秒）之间的关系如图所示（不完整）．据图中给出的信息，解答下列问题：

(1)、在上述变化过程中，自变量是，因变量是；

(2)、分别求朱老师和小明跑步的速度；

(3)、当小明追上朱老师时，求小明距起点的距离是多少米？

查看试题解析
23. 探究活动：

(1)、如图①，可以求出阴影部分的面积是（写成两数平方差的形式）；

(2)、如图②，若将图①中阴影部分裁剪下来，重新拼成一个长方形，面积是（写成多项式乘法的形式）；

(3)、比较图①，图②阴影部分的面积，可以得到公式．

(4)、计算：① $(a + b - 2 c) (a + b + 2 c)$ ；
② $(2 a + b - 3 c) (- 2 a + b + 3 c)$ ．

查看试题解析
24. 如图，在△ABC中，AB的垂直平分线MN交AB于点D，交AC于点E，且 $A C = 15 c m$ ， △BCE的周长等于 $24 c m$ ．

(1)、求BC的长；

(2)、若 $∠ A = 36 °$ ，并且 $A B = A C$ ．求证： $B C = B E$ ．

查看试题解析
25. 已知AB∥CD ，线段EF分别与AB、CD相交于点E、F ．

(1)、如图①，当∠A=20°，∠APC=70°时，求∠C的度数；

(2)、如图②，当点P在线段EF上运动时（不包括E、F两点），∠A、∠APC与∠C之间有怎样的数量？试证明你的结论；

(3)、如图③，当点P在直线EF上运动时，（2）中的结论还成立吗？如果成立，说明理由；如果不成立，直接写出它们之间的数量关系．（提示：三角形内角和为180°）

查看试题解析

所挂物重量 $x (k g)$	0	1	2	3	4	5
弹簧长度 $y (c m)$	20	22	24	26	28	30