贵州省黔东南州教学资源共建共享实验基地名校2022-2023学年七年级下学期数学期末考试试卷
试卷更新日期:2023-08-18 类型:期末考试
一、单选题
-
1. 下列给出的数中,是无理数的是( )A、 B、0 C、 D、2. 在平面直角坐标系中,已知点P(﹣2,3),则点P在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 以下调查中,最适合采用抽样调查的是( )A、学校招聘教师,对应聘人员进行面试 B、了解全班50名同学每天体育锻炼的时间 C、了解全国中学生的视力和用眼卫生情况 D、为保证神舟十四号载人飞船成功发射,对其零部件进行检查4. 不等式2x+3≥5的解集在数轴上表示正确的是( )
A、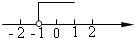 B、
B、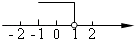 C、
C、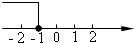 D、
D、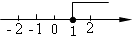 5. 如图,一把矩形直尺沿直线断开并错位,点E、D、B、F在同一条直线上.若 , 则的度数为( )
5. 如图,一把矩形直尺沿直线断开并错位,点E、D、B、F在同一条直线上.若 , 则的度数为( ) A、 B、 C、 D、6. 如图,将沿方向平移得到对应的 . 若 , 则的长是( )
A、 B、 C、 D、6. 如图,将沿方向平移得到对应的 . 若 , 则的长是( )
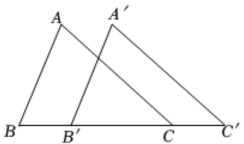 A、 B、 C、 D、7. 在矩形中, , , , 则点D的坐标为( )
A、 B、 C、 D、7. 在矩形中, , , , 则点D的坐标为( )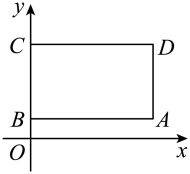 A、 B、 C、 D、8. 已知线段CD是由线段AB平移得到的,点A(–1,4)的对应点为C(4,7),则点B(–4,–1)的对应点D的坐标为( )A、(1,2) B、(2,9) C、(5,3) D、(–9,–4)9. 对于二元一次方程组 , 将①式代入②式,消去可以得到( )A、 B、 C、 D、10. 《九章算术》是中国传统数学名著,其中记载:“今有牛五、羊二,直金十两;牛二、羊五,直金八两.问牛、羊各直金几何?”译文:“假设有5头牛,2只羊,值金10两;2头牛,5只羊,值金8两.问每头牛、每只羊各值金多少两?”若设每头牛、每只羊分别值金x两、y两,则可列方程组为( )
A、 B、 C、 D、8. 已知线段CD是由线段AB平移得到的,点A(–1,4)的对应点为C(4,7),则点B(–4,–1)的对应点D的坐标为( )A、(1,2) B、(2,9) C、(5,3) D、(–9,–4)9. 对于二元一次方程组 , 将①式代入②式,消去可以得到( )A、 B、 C、 D、10. 《九章算术》是中国传统数学名著,其中记载:“今有牛五、羊二,直金十两;牛二、羊五,直金八两.问牛、羊各直金几何?”译文:“假设有5头牛,2只羊,值金10两;2头牛,5只羊,值金8两.问每头牛、每只羊各值金多少两?”若设每头牛、每只羊分别值金x两、y两,则可列方程组为( )
A、 B、 C、 D、11. 不等式组的整数解有三个,则的取值范围是( )A、 B、 C、 D、12. 在 , , , , 中,无理数的个数是( )A、44 B、45 C、1978 D、1979二、填空题
-
13. 要了解一批灯泡的使用寿命,从10000只灯泡中抽取60只灯泡进行试验,在这个问题中,样本容量是 .14. 已知直线过点 , 且与轴平行,直线过点 , 并与轴平行,则两直线的交点坐标是 .15. 如右图所示,已知直线、被所截,是的角平分线,若 , , 则的度数是 .
 16. 如图,在平面直角坐标系中,一动点从原点出发,按向上,向右,向下,向右的方向不断地移动,每移动一个单位,得到点 , , , , ……,那么点的坐标为 .
16. 如图,在平面直角坐标系中,一动点从原点出发,按向上,向右,向下,向右的方向不断地移动,每移动一个单位,得到点 , , , , ……,那么点的坐标为 .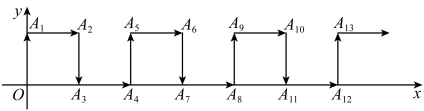
三、解答题
-
17.(1)、计算:;(2)、已知 , 求x的值.18.(1)、解方程组;(2)、解不等式组 , 请结合题意完成本题的解答(每空只需填出最后结果).
解:解不等式①,得 ▲ ,
解不等式②得 ▲ ,
把不等式①和②的解集在数轴上表示出来;

所以原不等式组解集为 ▲ .
19. 随着社会的发展,私家车变得越来越普及,使用节能低油耗汽车,被抽样的该型号汽车,在耗油1L的情况下所行驶的路程(单位:km),结果如图所示.
(注:记A为12~12.5,B为12.5~13,C为13~13.5,D为13.5~14,E为14~14.5)
请依据统计结果回答以下问题:
(1)、试求进行该试验的车辆数;(2)、请补全频数直方图;(3)、求扇形D的圆心角的度数.20. 某班去革命老区研学旅行,研学基地有甲乙两种快餐可供选择,买1份甲种快餐和2份乙种快餐共需70元,买2份甲种快餐和3份乙种快餐共需120元.(1)、买一份甲种快餐和一份乙种快餐各需多少元?(2)、已知该班共买55份甲乙两种快餐,所花快餐费不超过1280元,问至少买乙种快餐多少份?21. 补全下面的证明过程,并在括号内填上适当的理由.如图, , . 求证: .

证明:( )
( )
(已知),
▲ (对顶角相等)
( )
( )
22. 如图,在每个小正方形边长均为1个单位长度的方格中,有一个 , 每个顶点均与小正方形的顶点重合,且点 , .
请根据题意在图上建立平面直角坐标系;
在方格中,将向下平移5个单位长度,再向左平移2个单位长度得到 , 请画出 , 并写出点、、的坐标.
求的面积.
23. 如图, , , , 是的平分线.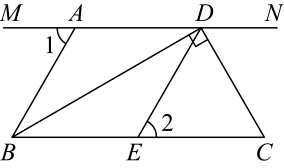 (1)、与平行吗?请说明理由;(2)、求的度数.24. 大家知道是无理数,而无理数是无限不循环小数,因此的小数部分我们不可能全部写出来,于是小明用来表示的小数部分,你同意小明的表示方法吗?
(1)、与平行吗?请说明理由;(2)、求的度数.24. 大家知道是无理数,而无理数是无限不循环小数,因此的小数部分我们不可能全部写出来,于是小明用来表示的小数部分,你同意小明的表示方法吗?事实上,小明的表示方法有道理、因为的整数部分是1,将减去其整数部分,差就是小数部分.
又例如:因为 , 即 , 所以的整数部分为2,小数部分为 .
根据以上内容,解答下列问题:
(1)、的整数部分是 , 小数部分是;(2)、如果的小数部分为a , 的整数部分为b , 求的值;(3)、已知 , 其中x是整数,且 , 求的值.25. 问题情境:如图1, , , , 求度数.小明的思路是:过作 , 通过平行线性质来求 .
 (1)、按小明的思路,易求得的度数为度;(直接写出答案)(2)、问题迁移:如图2, , 点在射线上运动,记 , , 当点在、两点之间运动时,问与、之间有何数量关系?请说明理由;(3)、在(2)的条件下,如果点在、两点外侧运动时(点与点、、三点不重合),请直接写出与、之间的数量关系.
(1)、按小明的思路,易求得的度数为度;(直接写出答案)(2)、问题迁移:如图2, , 点在射线上运动,记 , , 当点在、两点之间运动时,问与、之间有何数量关系?请说明理由;(3)、在(2)的条件下,如果点在、两点外侧运动时(点与点、、三点不重合),请直接写出与、之间的数量关系.