湖南省常德市鼎城区2022-2023学年七年级下学期数学期末考试试卷
试卷更新日期:2023-08-18 类型:期末考试
一、单选题
-
1. “认识交通标志,遵守交通规则”,下列交通标志中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列计算结果正确的是( )A、(a3)2=a6 B、a3•a2=a6 C、a3+a2=a5 D、(a-b)2=a2-b23. 在庆祝中国共产党成立100周年的校园歌唱比赛中,名参赛同学的成绩各不相同,按照成绩取前名进入决赛.如果小明知道了自己的比赛成绩,要判断能否进入决赛,小明需要知道这名同学成绩的( )A、中位数 B、众数 C、平均数 D、方差4. 已知是二元一次方程组的解,则( )A、6 B、8 C、10 D、115. 如图,将三角形绕点A逆时针旋转得到三角形 , 若 , 则的度数是( )
2. 下列计算结果正确的是( )A、(a3)2=a6 B、a3•a2=a6 C、a3+a2=a5 D、(a-b)2=a2-b23. 在庆祝中国共产党成立100周年的校园歌唱比赛中,名参赛同学的成绩各不相同,按照成绩取前名进入决赛.如果小明知道了自己的比赛成绩,要判断能否进入决赛,小明需要知道这名同学成绩的( )A、中位数 B、众数 C、平均数 D、方差4. 已知是二元一次方程组的解,则( )A、6 B、8 C、10 D、115. 如图,将三角形绕点A逆时针旋转得到三角形 , 若 , 则的度数是( ) A、 B、 C、 D、6. 如图,已知 , 若 , 则等于( )
A、 B、 C、 D、6. 如图,已知 , 若 , 则等于( ) A、 B、 C、 D、7. 当m为自然数时,一定能被下列哪个数整除( )A、 B、 C、 D、8. 如图,在三角形 , , 将三角形沿方向平移得到三角形 , 其中 , , , 则阴影部分的面积是( )
A、 B、 C、 D、7. 当m为自然数时,一定能被下列哪个数整除( )A、 B、 C、 D、8. 如图,在三角形 , , 将三角形沿方向平移得到三角形 , 其中 , , , 则阴影部分的面积是( ) A、15 B、18 C、21 D、不确定
A、15 B、18 C、21 D、不确定二、填空题
-
9. 计算: .10. 计算: .11. 小丹参加校园歌手比赛,唱功得90分,音乐常识得100分,综合知识得80分,学校按唱功、音乐常识、综合知识的5∶3∶2的比例计算总评成绩,那么小丹的总评成绩是 .12. 已知=0,则a+b=.13. 如图,已知相交于O , 于O , , 则的度数是 .
 14. 如图, , , 且三角形面积为12,则点C到的距离为 .
14. 如图, , , 且三角形面积为12,则点C到的距离为 . 15. 若 , , 则 .16. 某中学举行象棋比赛活动,通过抽签,甲、乙两名同学进行对弈,已知甲在6盘结束后,以净胜乙2分的成绩取胜,比赛的积分规则是:每盘比赛胜者得2分,负者得0分,和棋各得1分,则甲同学的总积分为 .
15. 若 , , 则 .16. 某中学举行象棋比赛活动,通过抽签,甲、乙两名同学进行对弈,已知甲在6盘结束后,以净胜乙2分的成绩取胜,比赛的积分规则是:每盘比赛胜者得2分,负者得0分,和棋各得1分,则甲同学的总积分为 .三、解答题
-
17. 计算:18. 因式分解:19. 解方程组:20. 先化简,再求值: , 其中 .21. 如图,已知三角形ABC和直线MN , 且三角形ABC的顶点在网格的交点上

画出三角形ABC向上平移4小格后的三角形A1B1C1;
画出三角形ABC关于直线MN成轴对称的三角形A2B2C2;
画出三角形ABC绕点B按逆时针方向旋转90°后的三角形A3BC3 .
22. 如图,直线 , 点在直线上,且 , , 求的度数.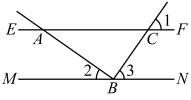 23. 如图,点E在直线上,点B在直线上,如果 , , 那么 .
23. 如图,点E在直线上,点B在直线上,如果 , , 那么 .
填空并填写理由:
解:因为(已知).
且( ).
所以(等量代换).
所以 ▲ ( ).
故( ).
又因为(已知),
所以 ▲ (等量代换).
所以( ).
所以( ).
24. 甲、乙两位同学5次参加“数学学科素养赛”选拔赛的成绩统计如表,他们5次测试的总成绩相同,请同学们完成下列问题:第1次
第2次
第3次
第4次
第5次
甲成绩
80
40
70
50
60
乙成绩
70
50
70
70
(1)、根据统计表求 , 甲同学成绩的中位数,乙同学成绩的众数;(2)、小林计算出甲同学的成绩平均数为60,方差是 . 请你求出乙同学成绩的平均数和方差;(3)、从平均数和方差的角度分析,甲、乙两位同学谁的成绩更稳定.25. 玲玲家准备装修一套新住房,若甲、乙两个装饰公司合作,需要6周完成,共需装修费5.2万元;若甲公司单独做4周后,剩下的由乙公司来做,还需9周才能完成,共需装修费4.8万元,玲玲的爸爸妈妈商量后决定只选一个公司单独完成.(1)、设工作总量为1,甲公司的每周工作效率为m , 乙公司每周的工作效率为n , 根据题意列出关于m、n的二元一次方程组.(2)、如果从节约时间的角度考虑,应选哪家公司?请说明理由.(3)、如果从节约开支的角度考虑,应选哪家公司?请说明理由.26. 已知直线 , 点P为直线 , 所确定的平面内的一点. (1)、问题提出:如图1, , , 求的度数;(2)、问题迁移:如图2,写出 , , 之间的数量关系,并说明理由;(3)、问题应用:如图3,点E在射线上,过点E作 , 作 , 点G在直线上,作的平分线交于点H , 若 , , 求的度数,不用写出计算过程.
(1)、问题提出:如图1, , , 求的度数;(2)、问题迁移:如图2,写出 , , 之间的数量关系,并说明理由;(3)、问题应用:如图3,点E在射线上,过点E作 , 作 , 点G在直线上,作的平分线交于点H , 若 , , 求的度数,不用写出计算过程.