甘肃省兰州市教育局第四片区2022-2023学年七年级下学期数学期末考试试卷

试卷更新日期：2023-08-18 类型：期末考试

进入出卷网下载

一、单选题

1. 2022年卡塔尔世界杯是第二十二届世界杯足球赛．下列四个图案是历届会徽图案上的一部分图形，其中轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 中国古代数学有着辉煌的成就，《周牌算经》《算学启蒙》《测圆海镜》《四元玉鉴》是我国古代数学的重要文献．某中学拟从这4部数学名著中选择1部作为校本课程“数学文化”的学习内容，恰好选中《算学启蒙》的概率是（）

A、 $\frac{1}{4}$ B、 $\frac{1}{2}$ C、 $\frac{1}{3}$ D、 $\frac{1}{6}$

查看试题解析
3. 若一个三角形两边的长分别为2和6，则这个三角形第三边的长可以是（）

A、3 B、4 C、6 D、9

查看试题解析
4. 下列说法中正确的是（　）

A、1000件产品中只有一件是次品，从中随机抽取一件，“是次品”是不可能事件 B、在装有红绿灯的十字路口，“遇到红灯”是随机事件 C、天气预报明天老河口有雨，“老河口明天下雨”是必然事件 D、从某校1000名男生中随机抽取2名进行引体向上测试，其中有一名成绩不及格，说明该校 $50 %$ 的男生引体向上成绩不及格

查看试题解析
5. 下列运算正确的是（）

A、 $m^{3} - m^{2} = m$ B、 $3 m^{2} \cdot 2 m^{3} = 6 m^{5}$ C、 $3 m^{2} + 2 m^{3} = 5 m^{5}$ D、 ${(2 m^{2})}^{3} = 8 m^{5}$

查看试题解析
6. 数学综合与实践小组的同学想测量一个池塘两端A ． B之间的距离，他门设计了如图所示的方案，在平地上选取能够直接到达点A和点B的一点C；连接 $B C$ 并延长，使 $C E = B C$ ；连接 $A C$ 并延长，使 $C D = A C$ ，连接 $D E$ 并测量其长度， $D E$ 的长度就是A、B之间的距离，此方案依据的数学定理或基本事实是（　　）

A、 $S A S$ B、 $S S S$ C、 $A S A$ D、 $A A S$

查看试题解析
7. 如图， $△ A B C$ 与 $△ A^{'} B^{'} C^{'}$ 关于直线l对称， $∠ A = 54 °$ ， $∠ C^{'} = 26 °$ ，则 $∠ B$ 等于（　　）

A、 $36 °$ B、 $154 °$ C、 $80 °$ D、 $100 °$

查看试题解析
8. 如图， $A B ∥ C D$ ，含 $30 °$ 的直角三角板的直角顶点在直线 $C D$ 上，若 $∠ E D C = 24 °$ ，则 $∠ A B E$ 的度数为（）

A、 $24 °$ B、 $30 °$ C、 $36 °$ D、 $45 °$

查看试题解析
9. 如图，直线 $l_{1} ∥ l_{2}$ ，点C、A分别在 $l_{1}$ 、 $l_{2}$ 上，以点C为圆心， $C A$ 长为半径画弧，交 $l_{1}$ 于点B ，连接 $A B$ 若 $∠ B C A = 130$ °，则∠1的度数为（）

A、 $15 °$ B、 $20 °$ C、 $25 °$ D、 $50 °$

查看试题解析
10. 如图， $O C$ 平分 $∠ A O B$ ，点P是射线 $O C$ 上一点， $P M ⊥ O B$ 于点M ，点N是射线 $O A$ 上的一个动点．若 $P M = 5$ ，则 $P N$ 的长度不可能是（　　）

A、5 B、6 C、7 D、4

查看试题解析
11. 下面的说法正确的个数为（　　）
①若 $∠ α = ∠ β$ ，则 $∠ α$ 和 $∠ β$ 是一对对顶角；

②若 $∠ α$ 与 $∠ β$ 互为补角，则 $∠ α + ∠ β = 180 °$ ；

③角平分线上的点到这个角的两边的距离相等；

④同旁内角相等，两直线平行．

A、1 B、2 C、3 D、4

查看试题解析
12. 如图，曲线表示一只蜜蜂在飞行过程中离地面的高度h（m）随飞行时间t（s）的变化而变化的情况，根据图象判断，下列说法正确的是（）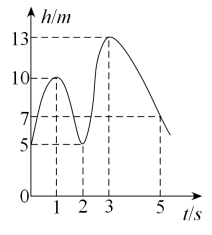

A、在这个变化过程中，h是自变量，t是因变量 B、飞行时间在1s～3s期间，蜜蜂距离地面的高度持续下降 C、飞行时间为4s时，蜜蜂距离地面的高度为15m D、在0s和2s时，蜜蜂距离地面的高度大致相同

查看试题解析

二、填空题

13. 近年来，我国研发的北斗芯片实现了22纳米制程的突破，22纳米等于0.000000022米．用科学记数法表示0.000000022是．

查看试题解析
14. 某家庭电话月租费为10元，若市内通话费平均每次为0.2元，则该家庭一个月的话费y（元）与通话次数x（次）之间的关系式是．

查看试题解析
15. 如图， $C D$ 是 $△ A B C$ 的高， $∠ A C B = 90 °$ ．若 $∠ A = 32 °$ ，则 $∠ B C D$ 的度数是．

查看试题解析
16. 如图，将一张长方形纸片按如图所示折叠，如果 $∠ 1 = 50 °$ ，那么 $∠ 2 =$ $°$ ．

查看试题解析

三、解答题

17. 计算：

(1)、 $(6 m^{3} n^{4} + 8 m^{2}) \div 2 m$ ；

(2)、 ${(- 1)}^{5} - | - 4 | + {(π - 3.14)}^{0} + {(\frac{1}{2})}^{- 3}$ ；

(3)、 ${(2 x^{3} y)}^{2} \cdot (- 2 x y^{2}) \div (- 2 x^{7} y^{2})$ ；

(4)、 $(9 x - 2 y) (x + y)$ ．

查看试题解析
18. 先化简，再求值： $x (x + 4) + (2 - x) (2 + x)$ ，其中 $x = 1$ ．

查看试题解析
19. 尺规作图：已知： $△ A B C$ ，求作： $△ D E F$ ，使得 $△ D E F ≌ △ A B C$ ．（保留作图痕迹，不写作法）

查看试题解析
20. 如图，在 $△ A B C$ 中， $A B = A C$ ，直线 $D E$ 垂直平分 $A B$ ，若 $∠ A = 40 °$ ，求 $∠ D B C$ 的度数．

查看试题解析
21. 如图，点C是 $A E$ 上一点， $C D$ 交 $E B$ 于点F， $C F = D F$ ， $E A ∥ D B$ ，求证： $E F = B F$ ．

查看试题解析
22. 如图，在每个小正方形的边长均为 $1$ 个单位长度的方格纸中，有 $△ A B C$ 和直线 $M N$ ，点 $A$ ， $B$ ， $C$ 均在小正方形的顶点（网格点）上．

$（ 1 ）$ 在方格纸中画出 $△ D B C$ ，使 $△ A B C$ 与 $△ D C B$ 关于直线 $M N$ 对称；

$（ 2 ）$ 在方格纸的网格点中找一点 $E$ ，使得 $C A = C E$ ，连接 $E A$ ， $E C$ ，并求出 $△ A C E$ 的面积．

查看试题解析
23. 如图，已知 $∠ B = ∠ E$ ， $A B = A E$ ， $∠ 1 = ∠ 2$ ．

(1)、求证： $△ A B C ≅ △ A E D$ ；

(2)、若 $∠ 1 = 40 °$ ，求 $∠ 3$ 的度数．

查看试题解析
24. 在一个不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共20只，某学习小组做摸球实验，将球搅匀后从中随机摸出一个球记下颜色，再把它放回袋中，不断重复，下表是活动进行中的一组统计数据：
摸球的次数 $n$
100
150
200
500
800
1000
摸到白球的次数 $m$
58
96
116
295
484
601
摸到白球的频率
$0.58$
$0.64$
$0.58$
$0.59$
$0.605$
$0.601$

(1)、请估计：当n很大时，摸到白球的频率将会接近；(精确到0.01)

(2)、假如你去摸一次，你摸到白球的概率是，摸到黑球的概率是；

(3)、试估算口袋中黑、白两种颜色的球各有多少只？

查看试题解析
25. 如图，小刚站在河边的点A处，在河对面（小刚的正北方向）的点B处有一电线塔，他想知道电线塔离他有多远，于是他向正西方向走了30步到达一棵树C处，接着再向前走了30步到达D处，然后他左转90°直行，从点D处开始计步，当小刚看到电线塔、树与自己现处的位置E在一条直线时，他恰好走了80步，并且小刚一步大约0.5米．由此小刚估计出了在点A处时他与电线塔的距离，请问他的做法是否合理？若合理，请求出在点A处时他与电线塔的距离；若不合理，请说明理由．

查看试题解析
26. 以点A为顶点作两个等腰直角三角形（△ABC，△ADE），如图1所示放置，使得一直角边重合，连接BD，CE．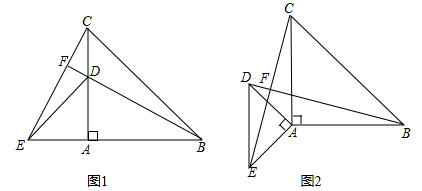

(1)、说明BD=CE；

(2)、延长BD，交CE于点F，求∠BFC的度数；

(3)、若如图2放置，上面的结论还成立吗？请简单说明理由．

查看试题解析

摸球的次数 $n$	100	150	200	500	800	1000
摸到白球的次数 $m$	58	96	116	295	484	601
摸到白球的频率	$0.58$	$0.64$	$0.58$	$0.59$	$0.605$	$0.601$