湖南省常德市澧县2022-2023学年七年级下学期数学期末考试试卷
试卷更新日期:2023-08-18 类型:期末考试
一、单选题
-
1. 下列方程组中,是二元一次方程组的是( )A、 B、 C、 D、2. 下列各图中,与是对顶角的是( )A、
 B、
B、 C、
C、 D、
D、 3. 下列计算正确的是( )A、 B、 C、 D、4. 王林是一位密码编译爱好者,在他的密码手册中有这样一条信息:分别对应六个字:县,爱,我,数,学,澧,现将因式分解,结果呈现的密码信息可能是( )A、我爱数学 B、爱澧县 C、我爱澧县 D、澧县数学5. 如图,下列条件中不能判定的是( )
3. 下列计算正确的是( )A、 B、 C、 D、4. 王林是一位密码编译爱好者,在他的密码手册中有这样一条信息:分别对应六个字:县,爱,我,数,学,澧,现将因式分解,结果呈现的密码信息可能是( )A、我爱数学 B、爱澧县 C、我爱澧县 D、澧县数学5. 如图,下列条件中不能判定的是( ) A、 B、 C、 D、6. 如图,某地进行城市规划,在一条新修公路MN旁有一村庄P,现要建一个汽车站,且有A,B,C,D四个地点可供选择.若要使汽车站离村庄最近,则汽车站应建在( )
A、 B、 C、 D、6. 如图,某地进行城市规划,在一条新修公路MN旁有一村庄P,现要建一个汽车站,且有A,B,C,D四个地点可供选择.若要使汽车站离村庄最近,则汽车站应建在( ) A、点A处 B、点B处 C、点C处 D、点D处7. 某校举办了以“红心颂党恩,喜迎二十大”为主题的演讲比赛.已知某位选手在演讲内容、演讲结构、演讲表达三项的得分分别为94分,80分,90分,若依次按照50%,30%,20%的百分比确定成绩,则该选手的成绩是( )A、85分 B、88分 C、89分 D、90分8. 如图,把长方形沿折叠后,点D,C分别落在 , 的位置.若 , 则是( )
A、点A处 B、点B处 C、点C处 D、点D处7. 某校举办了以“红心颂党恩,喜迎二十大”为主题的演讲比赛.已知某位选手在演讲内容、演讲结构、演讲表达三项的得分分别为94分,80分,90分,若依次按照50%,30%,20%的百分比确定成绩,则该选手的成绩是( )A、85分 B、88分 C、89分 D、90分8. 如图,把长方形沿折叠后,点D,C分别落在 , 的位置.若 , 则是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 二元一次方程组的解是.10. 分解因式: .11. 若 , , 则 .12. 甲、乙两人参加滑雪比赛,经过三轮初赛,他们的平均成绩相同.方差分别是 , ,则成绩更稳定的是(填“甲”或“乙”).13. 如图,将向右平移5个单位长度得到 , 且点B,E,C,F在同一条直线上,若 , 则的长度是 .
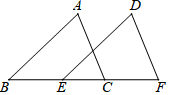 14. 如图, , , 为直线上的任意两点,则(用“ , , ”填写)
14. 如图, , , 为直线上的任意两点,则(用“ , , ”填写)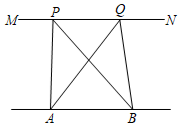 15. 如图,将△ABC绕点C顺时针旋转得到△CDE , 若点A恰好在ED的延长线上,若∠ABC=110°,则∠ADC的度数为 .
15. 如图,将△ABC绕点C顺时针旋转得到△CDE , 若点A恰好在ED的延长线上,若∠ABC=110°,则∠ADC的度数为 . 16. 如图,已知AB//CD,BE平分∠ABC,DE平分∠ADC,∠BAD=70°,∠BCD=40°,则∠BED的度数为.
16. 如图,已知AB//CD,BE平分∠ABC,DE平分∠ADC,∠BAD=70°,∠BCD=40°,则∠BED的度数为.
三、解答题
-
17. 先化简再求值: , 其中 , .18. 已知 , , 求的值.19. 某公司计划从两家皮具生产能力相近的制造厂选择一家来承担外销业务,这两家厂生产的皮具款式和材料都符合要求,因此只需要检测皮具质量的克数是否稳定.现从两家提供的样品中各抽查10件,测得它们的质量如下(单位:克)
甲:500,499,500,500,503,498,497,502,500,501,
乙:499,500,498,501,500,501,500,499,500,502
你认为该选择哪一家制造厂?
20. 看图填空(请将不完整的解题过程及依据补充完整):已知:如图, , , 试说明.

解:∵(已知),
∴ ▲ , (两直线平行,同位角相等)
又∵(已知)
∴∠ ▲ , ( )
∴ , ( )
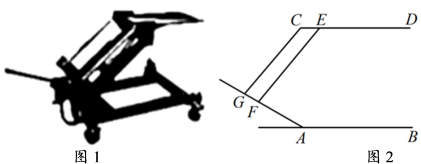
∴.( )
21. 如图1是一个由齿轮、轴承、托架等元件构成的手动变速箱托架,其主要作用是动力传输.如图2是手动变速箱托架工作时某一时刻的示意图,已知AB∥CD,CG∥EF,∠BAG=150°,∠AGC=80°,求∠DEF的度数.