吉林省长春市宽城区2022-2023学年七年级下学期数学期末考试试卷

试卷更新日期：2023-08-18 类型：期末考试

进入出卷网下载

一、单选题

1. 8的立方根为（）

A、 2 B、±2 C、－2 D、4

查看试题解析
2. 下列图形中，既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
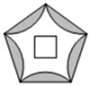3. 由 $3 < 5$ ，得 $3 x > 5 x$ ，则 $x$ 的值可能是（）

A、1 B、0.5 C、0 D、−1

查看试题解析
4. 如图，数轴上A、B两点到原点的距离是三角形两边的长，则该三角形第三边长可能是（）

A、1 B、4 C、7 D、8

查看试题解析
5. 我国古代《算法统宗》里有这样一首诗：“我问开店李三公，众客都来到店中，一房七客多七客，一房九客一房空.”诗中后面两句的意思是：如果一间客房住7人，那么有7人无房可住；如果一间客房住9人，那么就空出一间客房，若设该店有客房x间，房客y人，则列出关于x、y的二元一次方程组正确的是（）

A、 ${\begin{array}{l} 7 x - 7 = y \\ 9 (x - 1) = y \end{array}$ B、 ${\begin{array}{l} 7 x + 7 = y \\ 9 (x - 1) = y \end{array}$ C、 ${\begin{array}{l} 7 x + 7 = y \\ 9 x - 1 = y \end{array}$ D、 ${\begin{array}{l} 7 x - 7 = y \\ 9 x - 1 = y \end{array}$

查看试题解析
6. 用正三角形和正六边形镶嵌，若每一个顶点周围有m个正三角形、n 个正六边形，则m，n满足的关系式是( )

A、2m+3n=12 B、m+n=8 C、2m+n=6 D、m+2n=6

查看试题解析
7. 如图，点 $F$ ， $B$ ， $E$ ， $C$ 在同一条直线上， $△ A B C ≌ △ D E F$ ，若 $∠ A = 36 °$ ， $∠ F = 24 °$ ，则 $∠ D E C$ 的度数为（）

A、50° B、60° C、65° D、120°

查看试题解析
8. 五星红旗上的一个五角星图案如图所示，将图案绕五角星的中心至少旋转 $α$ 度能与自身重合，则 $α$ 为（）

A、108 B、90 C、72 D、60

查看试题解析

二、填空题

9. 化简 $\sqrt{12} =$ ．

查看试题解析
10. a与2的差不大于0，用不等式表示为．

查看试题解析
11. $m 、 n$ 是连续的两个整数，若 $m < \sqrt{6} < n$ ，则 $m + n$ 的值为．

查看试题解析
12. 一个多边形的外角和等于它的内角和，则这个多边形的边数是．

查看试题解析
13. 如图，在 $△ A B C$ 中， $E$ 是中线 $A D$ 的中点.若 $△ A E C$ 的面积是1，则 $△ A B D$ 的面积是.

查看试题解析
14. 如图，正五边形ABCDE和正六边形EFGHMN的边CD、FG在直线l上，正五边形在正六边形左侧，两个正多边形均在l的同侧，则 $∠ D E F$ 的大小是度．

查看试题解析

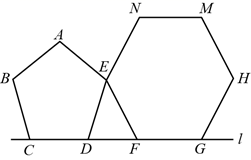
三、解答题

15. 计算： $\sqrt{25} - \sqrt[3]{27} + | - \sqrt{20} |$ ．

查看试题解析
16. 解方程组： ${\begin{array}{l} 2 x - y = 4 \\ 2 x + y + z = 1 \\ x - z = 5 \end{array}$

查看试题解析
17. 解不等式组： ${\begin{array}{l} x - 2 \leq 2 x ， \\ x - 1 < \frac{1 + 2 x}{3} ， \end{array}$ 并将解集在数轴上表示．

查看试题解析
18. 如图所示的正方形网格中，每个小正方形的顶点称为格点，每个小正方形的边长均为1个单位长度， $△ A B C$ 的三个顶点均在格点上，点O、M也在格点上．要求只用无刻度的直尺，在给定的网格中按要求画图．

$（ 1 ）$ 画出 $△ A B C$ 先向右平移5个单位长度，再向下平移5个单位长度后得到的 $△ A_{1} B_{1} C_{1}$ ．
$（ 2 ）$ 画出 $△ A B C$ 关于直线 $O M$ 对称的 $△ A_{2} B_{2} C_{2}$ ．
$（ 3 ）$ 画出 $△ A B C$ 绕点O按顺时针方向旋转 $90 °$ 后得到的 $△ A_{3} B_{3} C_{3}$ ，保留作图痕迹．

查看试题解析
19. 已知 $x - 2$ 的平方根是 $\pm 1$ ， $2 x + y + 6$ 的立方根是 $2$ ．

(1)、求 $x 、 y$ 的值．

(2)、求 $x^{2} + y^{2}$ 的平方根．

查看试题解析
20. 如图，在△ABC中，∠ACB＝∠ABC=2∠A，BD是AC边上的高，

(1)、求∠A的度数

(2)、求∠DBC的度数．

查看试题解析
21. 某公司要生产若干件新产品，需要精加工后，才能投放市场．现在甲、乙两个加工厂都想加工这批产品，已知甲工厂单独加工这批产品比乙工厂单独加工这批产品多用20天，甲工厂每天可加工16件产品，乙工厂每天可加工24件产品．

(1)、求这个公司要加工新产品的件数．

(2)、在加工过程中，公司需支付甲工厂每天加工费80元，乙工厂每天加工费120元．公司还需另派一名工程师每天到厂家进行技术指导，并负担每天5元的午餐补助费．公司制定产品加工方案如下：可由一个工厂单独加工完成，也可由两个工厂合作同时完成．当两个工厂合作时，这名工程师轮流去这两个工厂．请你通过计算帮助公司从所有可供选择的方案中选择一种既省钱，又省时间的加工方案．

查看试题解析
22. 如图，在 $△ A B C$ 中， $∠ A = 60 °$ ， $∠ A C B = 40 °$ ， $D$ 为 $B C$ 边延长线上一点， $B M$ 平分 $∠ A B C$ ， $E$ 为射线 $B M$ 上一点，连结 $C E$ ．

(1)、求 $∠ A B C$ 的度数．

(2)、若 $C E ∥ A B$ ，求 $∠ B E C$ 的度数．

(3)、若 $C E$ 平分 $∠ A C D$ ，求 $∠ B E C$ 的度数．

查看试题解析
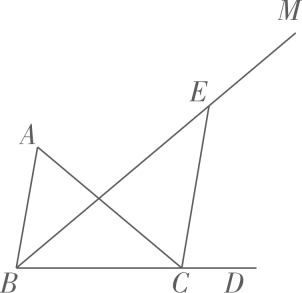23. 绍云中学计划为绘画小组购买某种品牌的A、B两种型号的颜料，若购买1盒A种型号的颜料和2盒B种型号的颜料需用56元；若购买2盒A种型号的颜料和1盒B种型号的颜料需用64元．

(1)、求每盒A种型号的颜料和每盒B种型号的颜料各多少元；

(2)、绍云中学决定购买以上两种型号的颜料共200盒，总费用不超过3920元，那么该中学最多可以购买多少盒A种型号的颜料？

查看试题解析
24. 如图，点O在直线 $A B$ 上， $O C ⊥ A B$ ．在 $△ O D E$ 中， $∠ O D E = 90 °$ ， $∠ E O D = 60 °$ ．先将 $△ O D E$ 的一边 $O E$ 与 $O C$ 重合，然后绕点O顺时针方向旋转，当 $O E$ 与 $O B$ 重合时停止旋转．

(1)、如图①，当 $O D$ 在 $O A$ 与 $O C$ 之间，且 $∠ C O D = 20 °$ 时，则 $∠ A O D =$ 度， $∠ C O E =$ 度．

(2)、如图②，当 $O D$ 在 $O C$ 与 $O B$ 之间时，求 $∠ A O D$ 与 $∠ C O E$ 差的度数．

(3)、在 $△ O D E$ 旋转的过程中，若 $∠ A O E = 7 ∠ C O D$ ，求旋转角的度数．

查看试题解析