江西省吉安市吉安县2022-2023学年七年级下学期数学期末考试试卷
试卷更新日期:2023-08-18 类型:期末考试
一、单选题
-
1. 下列计算正确的是( )A、 B、 C、 D、2. “共圆冰雪梦,一起向未来.”2022年2月4日至20日,第24届冬奥会将在中国北京和张家口举行.以下选取了四届冬奥会会标图案的一部分,其中是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 在党中央的坚强领导下,经过两年的战斗,新型冠状病毒引发的肺炎疫情得到了有效控制.研究发现,某种新型冠状病毒的直径约为213纳米,1纳米米,若用科学记数法表示213纳米,则正确的结果是( )A、米 B、米 C、米 D、米4. 下列事件为必然事件的是( )A、打开电视,它正在播广告 B、抛掷一枚硬币,正面朝上 C、367人中有生日相同的人 D、打雷后会下雨5. 如图,小明用铅笔可以支起一张质地均匀的三角形卡片,则他支起的这个点应是三角形的( )
3. 在党中央的坚强领导下,经过两年的战斗,新型冠状病毒引发的肺炎疫情得到了有效控制.研究发现,某种新型冠状病毒的直径约为213纳米,1纳米米,若用科学记数法表示213纳米,则正确的结果是( )A、米 B、米 C、米 D、米4. 下列事件为必然事件的是( )A、打开电视,它正在播广告 B、抛掷一枚硬币,正面朝上 C、367人中有生日相同的人 D、打雷后会下雨5. 如图,小明用铅笔可以支起一张质地均匀的三角形卡片,则他支起的这个点应是三角形的( )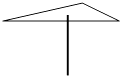 A、三边高的交点 B、三条角平分线的交点 C、三边垂直平分线的交点 D、三边中线的交点6. 小明观看了《中国诗词大会》第三期,主题为“人生自有诗意”,受此启发根据邻居家的故事写了一首小诗:“儿子学成今日返,老父早早到车站,儿子到后细端详,父子高兴把家还”,如图用y轴表示父亲与儿子行进中离家的距离,用x轴表示父亲离家的时间,那么下面图象与上述诗的含义大致相吻合的是( )A、
A、三边高的交点 B、三条角平分线的交点 C、三边垂直平分线的交点 D、三边中线的交点6. 小明观看了《中国诗词大会》第三期,主题为“人生自有诗意”,受此启发根据邻居家的故事写了一首小诗:“儿子学成今日返,老父早早到车站,儿子到后细端详,父子高兴把家还”,如图用y轴表示父亲与儿子行进中离家的距离,用x轴表示父亲离家的时间,那么下面图象与上述诗的含义大致相吻合的是( )A、 B、
B、 C、
C、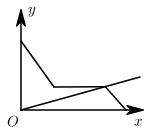 D、
D、
二、填空题
-
7. 如图,为了防止门板变形,小明在门板上钉了一根加固木条,请用数学知识说明这样做的依据.
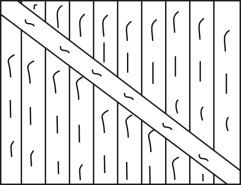 8. 在直角中, , 平分交于点D , 若 , 则点D到斜边的距离为 .
8. 在直角中, , 平分交于点D , 若 , 则点D到斜边的距离为 . 9. 若 , , 则 .10. 已知一等腰三角形的两边长分别为和 , 则此三角形的周长为 .11. 用每片长6cm的纸条,重叠1cm粘贴成一条纸带,如图.纸带的长度y(cm)与纸片的张数x之间的函数关系式是
9. 若 , , 则 .10. 已知一等腰三角形的两边长分别为和 , 则此三角形的周长为 .11. 用每片长6cm的纸条,重叠1cm粘贴成一条纸带,如图.纸带的长度y(cm)与纸片的张数x之间的函数关系式是 12. 等腰三角形一腰上的高与另一边的夹角为 , 这个三角形的各个内角的度数为 .
12. 等腰三角形一腰上的高与另一边的夹角为 , 这个三角形的各个内角的度数为 .三、解答题
-
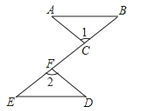
13. 计算:(1)、;(2)、先化简,再求值:化简并求值: . 其中 .14. 如图,点C,F在线段BE上,BF=EC,∠1=∠2,请你添加一个条件,使△ABC≌△DEF,并加以证明.(不再添加辅助线和字母)
 15. 某课题小组为了了解某品牌电动自行车的销售情况,对某专卖店第一季度该品牌A,B,C,D四种型号的销售做了统计,绘制成如下两幅统计图(均不完整)
15. 某课题小组为了了解某品牌电动自行车的销售情况,对某专卖店第一季度该品牌A,B,C,D四种型号的销售做了统计,绘制成如下两幅统计图(均不完整) (1)、该店第一季度售出这种品牌的电动自行车共多少辆?(2)、把两幅统计图补充完整;(3)、若该专卖店计划订购这四款型号的电动自行车1800辆,求C型电动自行车应订购多少辆?16. 作图题:
(1)、该店第一季度售出这种品牌的电动自行车共多少辆?(2)、把两幅统计图补充完整;(3)、若该专卖店计划订购这四款型号的电动自行车1800辆,求C型电动自行车应订购多少辆?16. 作图题:在如图所示的方格纸中不用量角器与三角尺,仅用直尺.

经过点 , 画线段平行于所在直线.
过点 , 画线段垂直于所在直线.
17. 如图,AD∥BC,FC⊥CD,∠1=∠2,∠B=60°.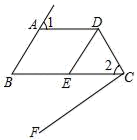 (1)、求∠BCF的度数;(2)、如果DE是∠ADC的平分线,那么DE与AB平行吗?请说明理由.18. 如图,大小两个正方形边长分别为a、b.
(1)、求∠BCF的度数;(2)、如果DE是∠ADC的平分线,那么DE与AB平行吗?请说明理由.18. 如图,大小两个正方形边长分别为a、b. (1)、用含a、b的代数式阴影部分的面积S;(2)、如果a+b=7,ab=5,求阴影部分的面积.19. 公路上依次有A,B,C三个汽车站,上午8时,小明骑自行车从A,B两站之间距离A站8km处出发,向C站匀速前进,他骑车的速度是每小时16.5km,若A,B两站间的路程是26km,B,C两站的路程是15km.(1)、在小明所走的路程与骑车用去的时间这两个变量中,哪个是自变量?哪个是因变量?(2)、设小明出发x小时后,离A站的路程为ykm,请写出y与x之间的关系式.(3)、小明在上午9时是否已经经过了B站?20. 如图,中,D为的中点,厘米,厘米.
(1)、用含a、b的代数式阴影部分的面积S;(2)、如果a+b=7,ab=5,求阴影部分的面积.19. 公路上依次有A,B,C三个汽车站,上午8时,小明骑自行车从A,B两站之间距离A站8km处出发,向C站匀速前进,他骑车的速度是每小时16.5km,若A,B两站间的路程是26km,B,C两站的路程是15km.(1)、在小明所走的路程与骑车用去的时间这两个变量中,哪个是自变量?哪个是因变量?(2)、设小明出发x小时后,离A站的路程为ykm,请写出y与x之间的关系式.(3)、小明在上午9时是否已经经过了B站?20. 如图,中,D为的中点,厘米,厘米. (1)、若点P在线段上以3厘米/秒的速度从点B向终点C运动,同时点Q在线段上从点C向终点A运动,若点Q的速度与点P的速度相等,经1秒钟后,请说明;(2)、若点P以3厘米/秒的速度从点B向点C运动,同时点Q以5厘米/秒的速度从点C向点A运动,它们都依次沿三边运动,则经过多长时间,点Q第一次在的哪条边上追上点P?21. 点O为直线上一点,过点O作射线 , 使 , 一直角三角板的直角顶点放在点O处.
(1)、若点P在线段上以3厘米/秒的速度从点B向终点C运动,同时点Q在线段上从点C向终点A运动,若点Q的速度与点P的速度相等,经1秒钟后,请说明;(2)、若点P以3厘米/秒的速度从点B向点C运动,同时点Q以5厘米/秒的速度从点C向点A运动,它们都依次沿三边运动,则经过多长时间,点Q第一次在的哪条边上追上点P?21. 点O为直线上一点,过点O作射线 , 使 , 一直角三角板的直角顶点放在点O处. (1)、如图1,将三角板的一边与射线重合时,则;(2)、如图2,将图1中的三角板绕点O逆时针旋转一定角度,当恰好是的角平分线时,求的度数;(3)、将图1中的三角尺绕点O逆时针旋转的过程中,设旋转的角度为度,在旋转的过程中,能否使?若能,求出的度数;若不能,说明理由.22. 【知识生成】通常,用两种不同的方法计算同一个图形的面积,可以得到一个恒等式.
(1)、如图1,将三角板的一边与射线重合时,则;(2)、如图2,将图1中的三角板绕点O逆时针旋转一定角度,当恰好是的角平分线时,求的度数;(3)、将图1中的三角尺绕点O逆时针旋转的过程中,设旋转的角度为度,在旋转的过程中,能否使?若能,求出的度数;若不能,说明理由.22. 【知识生成】通常,用两种不同的方法计算同一个图形的面积,可以得到一个恒等式.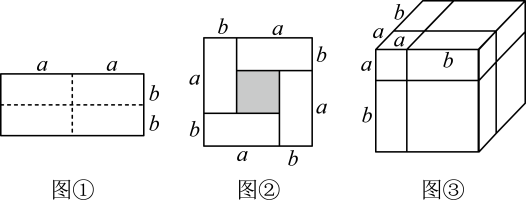
例如:如图①是一个长为 , 宽为的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图②的形状拼成一个正方形.请解答下列问题:
(1)、请用两种不同的方法求图②中阴影部分的面积:方法1:;
方法2:;
由此可以得出、、之间的等量关系是;
(2)、根据图③,写出一个代数恒等式:;(3)、已知 , , 利用上面的规律求的值.23. 已知点C为线段上一点,分别以为边在线段同侧作和 , 且 , 直线与交于点F. (1)、如图①,求证:;(2)、如图①,若 , 则=°;如图②,若 , 则=°;
(1)、如图①,求证:;(2)、如图①,若 , 则=°;如图②,若 , 则=°;如图③,若 , 则=°;
(3)、如图④,若 , 则°(用含的代数式表示);(4)、若A、B、C三点不在同一直线上,线段与线段交于点C(交点F至少在中的一条线段上),如图⑤,若 , 试判断与的数量关系,并说明理由.