吉林省四平市铁西区2022-2023学年七年级下学期数学期末考试试卷

试卷更新日期：2023-08-18 类型：期末考试

进入出卷网下载

一、单选题

1. 下列图形中，∠1和∠2是邻补角的是（）

A、 B、 C、 D、

查看试题解析
2. 下列调查中，最适合采用全面调查的是（）

A、了解全国中学生的睡眠时间 B、了解某河流的水质情况 C、调查全班同学的视力情况 D、对某池塘中现有鱼的数量的调查

查看试题解析
3. 若 $m > n$ ，则下列不等式中错误的是（）

A、 $m - 4 > n - 4$ B、 $\frac{m}{2} > \frac{n}{2}$ C、 $m + 5 > n + 5$ D、 $- \frac{m}{2} > - \frac{n}{2}$

查看试题解析
4. 由 $x - 3 y = 5$ ，得到用x表示y的式子为（）

A、 $y = 3 x - 15$ B、 $y = \frac{1}{3} x - \frac{5}{3}$ C、 $y = \frac{1}{3} x + \frac{5}{3}$ D、 $y = - 3 x + 15$

查看试题解析
5. 如图①，一个容量为500mL的杯子中装有200mL的水，将四颗相同的玻璃球放入这个杯中，结果水没有满，如图②，设每颗玻璃球的体积为 $x c m^{3}$ ，根据题意可列不等式为（）

A、 $200 + 4 x < 500$ B、 $200 + 4 x ≤ 500$ C、 $200 + 4 x > 500$ D、 $200 + 4 x ≥ 500$

查看试题解析
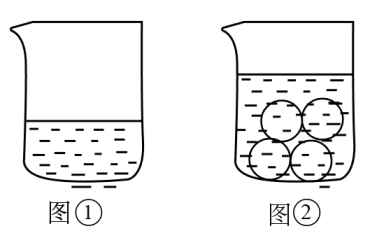6. 解方程组 ${\begin{array}{l} 2 x + 3 y = 8 ， \\ 3 x - 2 y = - 1 \end{array}$ 的思路可用如图的框图表示，圈中应填写的对方程①②所做的变形为（）

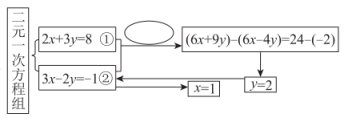A、①×2+②×3 B、①×2-②×3 C、①×3-②×2 D、①×3+②×2

查看试题解析

二、填空题

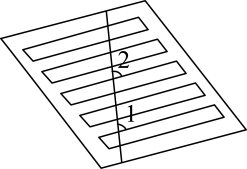
7. 16的算术平方根是

查看试题解析
8. 用不等式表示“a的2倍与b的和不大于3”：．

查看试题解析
9. 若点 $M (2 m - 6 ， m - 1)$ 在y轴上，则点M的坐标为．

查看试题解析
10. 不等式 $x - 1 < 2$ 的最大整数解是．

查看试题解析
11. 斑马线的作用是为了引导行人安全地通过马路．某数学兴趣小组为了验证斑马线是由若干条平行线组成的，在保证安全的前提下，按照如图方式分别测出 $∠ 1 = ∠ 2 = 85 °$ ，这种验证方法的数学依据是．

查看试题解析
12. 在一个样本中，40个数据分别落在5个小组内，第1，2，3，5小组的频数分别是2，8，15，5，则第4小组的频数是．

查看试题解析
13. 若 ${\begin{array}{l} x = - 1 \\ y = 2 \end{array}$ 是二元一次方程 $2 y - a x = - 5$ 的一个解，则a的值为．

查看试题解析
14. 若关于x的一元一次不等式组 ${\begin{array}{l} x - 1 < 3 \\ x - a < 0 \end{array}$ 的解集为 $x < 4$ ，则a的取值范围是．

查看试题解析

三、解答题

15. 解方程组： ${\begin{cases} x + y = 7 \\ 3 x + y = 17 \end{cases}$ ；

查看试题解析
16. 解方程组： ${\begin{array}{l} 2 x + 3 y = - 1 \\ 3 x - 2 y = 18 \end{array}$ ．

查看试题解析
17. 解不等式： $\frac{3 x - 2}{4} - 1 \leq \frac{5 x - 7}{6}$ ．

查看试题解析
18. 解不等式组： ${\begin{array}{l} \frac{x + 1}{2} > x - 1 ① \\ 3 (x + 2) \geq 2 (x + 3) ② \end{array}$ 并把解集在数轴上表示出来．

查看试题解析
19. 已知一个正数的两个平方根分别是 $2 a - 3$ 和 $5 - a$ ， $b - 1$ 的算术平方根为2， $c$ 是 $\sqrt{19}$ 的整数部分，

(1)、求a、b、c的值．

(2)、求 $a + b - c$ 的立方根．

查看试题解析
20. 如图所示，已知 $A D ⊥ B C$ 于点D ， $F E ⊥ B C$ 于点E ，交 $A B$ 于点G ，交 $C A$ 的延长线于点F ，且 $∠ 1 = ∠ 2$ ．问： $A D$ 平分 $∠ B A C$ 吗？并说明理由．

查看试题解析
21. 在平面直角坐标系 $x O y$ 中， $A (2 ， - 1)$ ， $B (4 ， 3)$ ．将线段 $A B$ 先向左平移3个单位，再向下平移1个单位得到线段 $C D$ （其中点A的对应点为点C ，点B的对应点为点D），线段 $C D$ 恰好过点O ．线段 $A B$ 上的点E平移后的对应点为点O ．

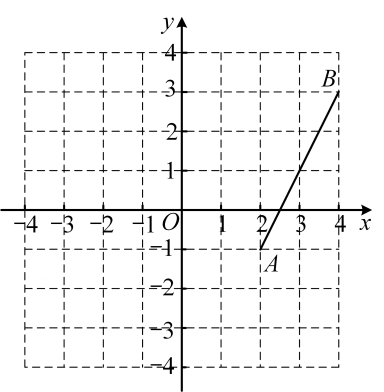(1)、画出线段 $C D$ ；

(2)、直接写出点C和点E的坐标；

(3)、画出四边形 $B D C E$ ；

(4)、直接写出四边形 $B D C E$ 的面积．

查看试题解析
22. 星期天，小明骑自行车去姥姥家，速度为每小时 $12 k m$ ，出发1小时后，小明的爸爸发现小明忘记带家里的钥匙，立即骑摩托车去送，小明的爸爸至少以怎样的速度，才能在20分钟内追上小明？

查看试题解析
23.

(1)、已知关于 $x$ 方程 $3 k - 5 x = - 9$ 的解是非负数，求 $k$ 的取值范围．

(2)、若关于 $x$ 、 $y$ 的方程组 ${\begin{array}{l} 2 x + 3 y = m \\ 3 x + 5 y = m + 2 \end{array}$ 的解满足 $x - y \geq 5$ ，求 $m$ 的最小整数值．

查看试题解析
24. 已知 $∠ X O Y = 2 α (0 ° < α < 45 °)$ ，点A在射线 $O X$ 上，点P在 $∠ X O Y$ 外部， $P A ∥ O Y$ ， $∠ P = \frac{1}{2} ∠ X O Y$ ，它另一边交射线 $O X$ 于点M ，交射线 $O Y$ 于点B ，点C在线段 $B A$ 的延长线上．

(1)、如图，若 $∠ P A C = 40 °$ ， $∠ P B C = 20 °$ ，则 $α =$ °；

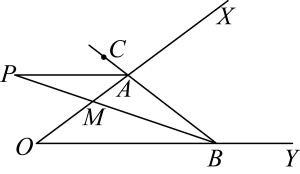(2)、若 $A P$ 平分 $∠ O A C$ ，求证： $B P$ 平分 $∠ O B C$ ；

(3)、当 $P M ⊥ O A$ 时，请直接写出 $α$ 的度数．

查看试题解析
25. 四平市为了更好地适应城市绿化的需求，决定购买东风多利卡雾炮抑尘洒水车，这种洒水车有 $D 7$ 型和 $D 9$ 型两种型号．已知购买一辆 $D 9$ 型洒水车比购买一辆 $D 7$ 型洒水车多2万元，购买2辆 $D 9$ 型洒水车比购买3辆 $D 7$ 型洒水车少 $9.5$ 万元．

(1)、分别求购买一辆 $D 9$ 型洒水车和 $D 7$ 型洒水车的钱数．

(2)、若市政决定购买多利卡雾炮抑尘洒水车共10辆，购买洒水车的总金额不超过140万元，请你为市政设计购买方案，并说明理由．

查看试题解析
26. 如图，在平面直角坐标系中，已知 $A (0 ， a)$ ， $B (b ， 0)$ ， $C (4 ， c)$ 三点，其中 $a 、 b 、 c$ 满足关系式： $| a - 3 | + {(b - 4)}^{2} + \sqrt{c - 5} = 0$ ．

(1)、求 $a 、 b 、 c$ 的值；

(2)、请直接判断 $B C$ 与y轴的位置关系；

(3)、若平面内有一点 $P (m ， \frac{1}{3})$ ，且点P到 $B C$ 的距离为5，请求出 $△ A O P$ 的面积；

(4)、如果点 $P (m ， \frac{1}{3})$ 在第二象限内，是否存在负整数m ，使四边形 $A B O P$ 的面积不小于 $△ A O P$ 面积的3倍？若存在，请直接写出所有满足条件的点P的坐标，若不存在，请说明理由．

查看试题解析