江西省吉安市遂川县2022-2023学年七年级下学期数学期末考试试卷
试卷更新日期:2023-08-18 类型:期末考试
一、单选题
-
1. 计算 的结果是( )A、 B、 C、 D、2. 已知一个角的度数为 , 则下列角中,与已知角的度数为互补关系的可能是( )A、
 B、
B、 C、
C、 D、
D、 3. 下列四所世界名牌大学的校徽图案,是轴对称图形的个数是( )
3. 下列四所世界名牌大学的校徽图案,是轴对称图形的个数是( ) A、1个 B、2个 C、3个 D、4个4. 下列运算中,正确的是( )A、 B、 C、 D、5. 如果一个三角形的两个内角分别为和 , 则这个三角形的形状是( )A、锐角三角形 B、直角三角形 C、钝角三角形 D、无法判断6. 某地美丽乡村建设中,对某一路段进行硬化,如图是某日上午4小时硬化公路长l(单位:m)与施工时间t(单位:h)的函数关系的图象,则下列说法正确的是( )
A、1个 B、2个 C、3个 D、4个4. 下列运算中,正确的是( )A、 B、 C、 D、5. 如果一个三角形的两个内角分别为和 , 则这个三角形的形状是( )A、锐角三角形 B、直角三角形 C、钝角三角形 D、无法判断6. 某地美丽乡村建设中,对某一路段进行硬化,如图是某日上午4小时硬化公路长l(单位:m)与施工时间t(单位:h)的函数关系的图象,则下列说法正确的是( ) A、施工队休息了 B、休息后施工速度为 C、两个时间段修建的公路长相等 D、休息前后每小时修建的公路长相等
A、施工队休息了 B、休息后施工速度为 C、两个时间段修建的公路长相等 D、休息前后每小时修建的公路长相等二、填空题
-
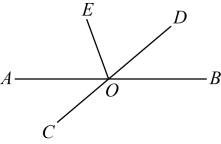
7. 已知 , 则的余角的度数为 .8. 人体最小的细胞是淋巴细胞,直径约为0.0000061m,用科学记数法可将0.0000061表示为 .9. 在变量x与y的关系式中,当自变量时,因变量y的值为 .10. 若 , 则的值为 .11. 如图,直线与交于点O , 平分 , 若 , 则的度数为 .
 12. 在中, , , 点P是上一动点,当为等腰三角形时,的度数为 .
12. 在中, , , 点P是上一动点,当为等腰三角形时,的度数为 .
三、解答题
-
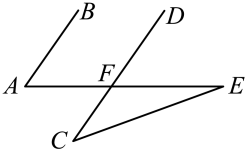
13.(1)、计算:;(2)、如图, , 交于点F , , , 求的度数.
 14. 一个三角形的三个内角的度数之比为1:3:5,判断这个三角形的形状.15. 先化简,再求值: , 其中 , .16. 如图是正方形网格,请仅用无刻度的直尺按下列要求作图.
14. 一个三角形的三个内角的度数之比为1:3:5,判断这个三角形的形状.15. 先化简,再求值: , 其中 , .16. 如图是正方形网格,请仅用无刻度的直尺按下列要求作图. (1)、在图1中,作的平分线;(2)、在图2中,作的边上的高.17. 如图,已知 , , , 点E在上,点F在的延长线上.求证: .
(1)、在图1中,作的平分线;(2)、在图2中,作的边上的高.17. 如图,已知 , , , 点E在上,点F在的延长线上.求证: . 18. 一个正方体的棱长为 , 求它的底面周长和体积.19. 一个不透明的袋中装有2个红球、3个黄球和1个白球,它们除颜色外都相同.(1)、从中随机取出一个球是红球是事件,随机取出一个球是黑球是事件;(2)、求从袋中任意摸出一个球是黄球的概率.20. 如图,已知直线 , 相交于点O , 是射线, , 比大 , 求的度数.
18. 一个正方体的棱长为 , 求它的底面周长和体积.19. 一个不透明的袋中装有2个红球、3个黄球和1个白球,它们除颜色外都相同.(1)、从中随机取出一个球是红球是事件,随机取出一个球是黑球是事件;(2)、求从袋中任意摸出一个球是黄球的概率.20. 如图,已知直线 , 相交于点O , 是射线, , 比大 , 求的度数. 21. 一菜农带了若干千克的土豆进城出售,为了方便,他带了一些零钱备用.在市场先售出一些后,又降价出售.售出土豆千克数x与他手中持有的钱数y(含备用零钱)的关系如图所示,结合图像回答下列问题:
21. 一菜农带了若干千克的土豆进城出售,为了方便,他带了一些零钱备用.在市场先售出一些后,又降价出售.售出土豆千克数x与他手中持有的钱数y(含备用零钱)的关系如图所示,结合图像回答下列问题: (1)、农民自带的零钱是元;(2)、求降价前他每千克土豆出售的价格;(3)、降价后他按每千克0.8元将剩余的土豆售完,这时他手中的钱(含备用的钱)是66元,问进城时他一共带了多少千克的土豆?22. 七年级某班数学小组研究系列算式: , , . ...,将算式计算过程进行变形后,得到如下规律:
(1)、农民自带的零钱是元;(2)、求降价前他每千克土豆出售的价格;(3)、降价后他按每千克0.8元将剩余的土豆售完,这时他手中的钱(含备用的钱)是66元,问进城时他一共带了多少千克的土豆?22. 七年级某班数学小组研究系列算式: , , . ...,将算式计算过程进行变形后,得到如下规律:;
;
;
……
(1)、根据以上规律,直接写出的相应变形算式;(2)、请用含n的代数式直接表示与之积的计算结果,并通过计算验证结果的正确性.23. 某数学小组在探究角平分线上的点与角的顶点、以及射线上的点构建等腰三角形的问题中,经历了如下过程:
如图,为内部的一点,平分 , 是的边上的点,连接 , 分别以 , 为腰向右侧作等腰和等腰 , 使得 , , 交于点 , 且 .
(1)、问题发现当时,的度数为 , 的度数为 .
(2)、猜想论证当时,与存在什么数量关系?请说明理由.
(3)、拓展思考设 , 当与满足什么数量关系时,点落在的下方?直接写出数量关系,不必说明理由.