山西省晋城市阳城县2022-2023学年七年级下学期数学期末考试试卷
试卷更新日期:2023-08-18 类型:期末考试
一、单选题
-
1. 若 , 则a等于( )A、 B、1 C、2 D、2. 下列图案中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 不等式2x≤4的解集在数轴上表示正确的是( )A、
3. 不等式2x≤4的解集在数轴上表示正确的是( )A、 B、
B、 C、
C、 D、
D、 4. 若 , 则下列不等式一定成立的是( )A、 B、 C、 D、5. 《孙子算经》中有“鸡兔同笼”问题:“今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔各几何.”设鸡有x只,可列方程为( )A、 B、 C、 D、6. 某学校七年级2班学生杨冲家和李锐家到学校的直线距离分别是和 . 那么杨冲,李锐两家的直线距离不可能是( )A、 B、 C、 D、7. 如图,为的中线,E为的中点,若的面积为12,则阴影部分的面积为( )
4. 若 , 则下列不等式一定成立的是( )A、 B、 C、 D、5. 《孙子算经》中有“鸡兔同笼”问题:“今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔各几何.”设鸡有x只,可列方程为( )A、 B、 C、 D、6. 某学校七年级2班学生杨冲家和李锐家到学校的直线距离分别是和 . 那么杨冲,李锐两家的直线距离不可能是( )A、 B、 C、 D、7. 如图,为的中线,E为的中点,若的面积为12,则阴影部分的面积为( ) A、24 B、8 C、12 D、68. 如图,AC⊥BE , DE⊥BE , 若△ABC≌△BDE , AC=5,DE=2,则CE等于( )
A、24 B、8 C、12 D、68. 如图,AC⊥BE , DE⊥BE , 若△ABC≌△BDE , AC=5,DE=2,则CE等于( )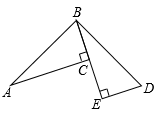 A、2.5 B、3 C、3.5 D、49. 把边长相等的正五边形和正六边形按照如图的方式叠合在一起,是正六边形的对角线,则等于( )
A、2.5 B、3 C、3.5 D、49. 把边长相等的正五边形和正六边形按照如图的方式叠合在一起,是正六边形的对角线,则等于( ) A、 B、 C、 D、10. 如图,已知的内角 , 分别作内角与外角的平分线,两条平分线交于点 , 得;和的平分线交于点 , 得; , 以此类推得到 , 则的度数是( )
A、 B、 C、 D、10. 如图,已知的内角 , 分别作内角与外角的平分线,两条平分线交于点 , 得;和的平分线交于点 , 得; , 以此类推得到 , 则的度数是( )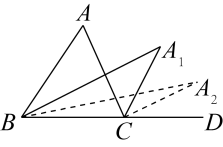 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 已知一个正多边形的一个外角为 , 则这个正多边形的边数是 .12. 如图是《九章算术》中的算筹图,图中各行从左到右列出的算筹数分别表示未知数 , 的系数与相应的常数项.如下图所示的算筹图用方程组形式表述出来,就是 .
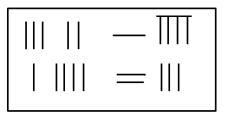
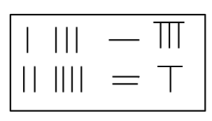
类似地,下图所示的算筹图,可以表述为 .
 13. 小明家装修房屋,想用一种正多边形瓷砖铺地,顶点连着顶点,彼此之间不留空隙又不重叠,请你帮助他选择一种能密铺的瓷砖形状 . (写出一种即可)14. 如图,P是正△ABC内的一点,若将△PAB绕点A逆时针旋转到△P1AC , 则∠PAP1等于度.
13. 小明家装修房屋,想用一种正多边形瓷砖铺地,顶点连着顶点,彼此之间不留空隙又不重叠,请你帮助他选择一种能密铺的瓷砖形状 . (写出一种即可)14. 如图,P是正△ABC内的一点,若将△PAB绕点A逆时针旋转到△P1AC , 则∠PAP1等于度. 15. 如图,中, , , 将其折叠,使点A落在边上处,折痕为 , 则的度数为 .
15. 如图,中, , , 将其折叠,使点A落在边上处,折痕为 , 则的度数为 . 16. 如图,两个全等的直角三角形重叠在一起,将其中一个直角三角形沿的方向平移,平移的距离为线段的长,则阴影部分的面积为 .
16. 如图,两个全等的直角三角形重叠在一起,将其中一个直角三角形沿的方向平移,平移的距离为线段的长,则阴影部分的面积为 .
三、解答题
-
17. 按要求计算下列各题(1)、解方程:(2)、求不等式组的所有整数解.18. 课堂上老师出了一道题目:解方程组(1)、小组学习时,老师发现有同学这么做:
得,③,
得, ,
∴
把代入①得 ∴这个方程组的解是
该同学解这个方程组的过程中使用了消元法,目的是把二元一次方程组转化为 , 这种解题方法主要体现了的数学思想.
(2)、请用另一种方法(代入消元法)解这个方程组.19. 如图,已知正方形的边长是2,点E在上,经顺时针旋转后与重合. (1)、指出旋转的中心和旋转的角度;(2)、向右平移后与重合,平移的距离是多少?(3)、连接 , 那么是什么三角形?请说明理由.20. 在下图的正方形网格中,每个小正方形的边长都是单位1,的顶点均在格点上.
(1)、指出旋转的中心和旋转的角度;(2)、向右平移后与重合,平移的距离是多少?(3)、连接 , 那么是什么三角形?请说明理由.20. 在下图的正方形网格中,每个小正方形的边长都是单位1,的顶点均在格点上.
画出关于直线对称的;
画出 , 使与关于点O成中心对称;
与是否成轴对称.若是,请在图中画出对称轴.
21. 倡导健康生活,推进全民健身,某社区要购进A,B两种型号的健身器材若干套,A,B两种型号健身器材的购买单价分别为每套310元,460元,且每种型号健身器材必须整套购买.(1)、若购买A,B两种型号的健身器材共50套,且恰好支出20000元,求A,B两种型号健身器材各购买多少套?(2)、若购买A,B两种型号的健身器材共50套,且支出不超过18000元,求A种型号健身器材至少要购买多少套?22. 阅读下列材料,并完成相应的任务:有趣的“飞镖图”.如图1的四边形 , 这种形似飞镖的四边形,我们形象地称它为“飞镖图”.它实际上就是凹四边形,同学们通过探究发现:凹四边形中最大内角外面的角等于其余三个内角之和,即如图1, .
“智慧小组”通过互学证明了这个结论:
方法一:如图2,连接 , 则在中, ,
即 ,
又:在中, ,
∴ ,
即 .
“创新小组”想出了另外一种方法
方法二:如图3,连接并延长至F ,
∵和分别是和的一个外角,
……
……
任务:
(1)、填空:“智慧小组”用的“方法一”主要依据的一个数学定理是;(2)、根据“创新小组”用的“方法二”中辅助线的添加方式,写出该证明过程的剩余部分.23. 如图1,将一副直角三角板放在同一条直线上,其中 , . (1)、观察猜想:将图1中的三角尺沿的方向平移至图2的位置,使得点O与点N重合,与相交于点E,则;(2)、操作探究:将图1中的三角尺绕点O按顺时针方向旋转,使一边在的内部,如图3,且OD恰好平分 , 与相交于点E,求的度数;(3)、深化拓展:将图1中的三角尺绕点O按沿顺时针方向旋转一周,在旋转的过程中,当边旋转多少度时,边恰好与边平行?
(1)、观察猜想:将图1中的三角尺沿的方向平移至图2的位置,使得点O与点N重合,与相交于点E,则;(2)、操作探究:将图1中的三角尺绕点O按顺时针方向旋转,使一边在的内部,如图3,且OD恰好平分 , 与相交于点E,求的度数;(3)、深化拓展:将图1中的三角尺绕点O按沿顺时针方向旋转一周,在旋转的过程中,当边旋转多少度时,边恰好与边平行?