山西省大同市2022-2023学年七年级下学期数学期末考试试卷
试卷更新日期:2023-08-18 类型:期末考试
一、单选题
-
1. 27的立方根是( )A、3 B、 C、 D、2. 下列调查中,适合采用全面调查的是( )A、了解某品牌某型号新能源汽车的最大续航里程 B、了解端午节期间去云冈石窟游览的游客的满意度 C、了解某班50名同学的视力情况 D、了解汾河太原城区段的水质情况3. 如图, , 交于点 , 若 , 则的度数为( )
 A、 B、 C、 D、4. 用代入法解方程组 时,代入正确的是( )A、x-2-x=4 B、x-2-2x=4 C、x-2+2x=4 D、x-2+x=45. 若 , , 则下列结论正确的是( )A、 B、 C、 D、6. 将点向右平移个单位长度得到点 , 则点所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限7. 若不等式组的解集是 , 则不等式②可以是( )A、 B、 C、 D、8. 我国清代算书《御制数理精蕴》(卷九)中有这样一题:“设如有甲、乙二人人山采果共得三百枚,但云甲数加六百枚,乙数加二百枚,则甲数比乙数多二倍.问甲、乙各得几何.”设甲数为枚,乙数为枚,根据题意可列方程组为( )A、 B、 C、 D、9. 某学校计划在七年级开设折扇、刺绣、剪纸、陶艺四门校本课程,要求每人必须参加,并且只能选择其中一门课程,为了解学生对这四门课程的选择情况,学校从七年级全体学生中随机抽取部分学生进行问卷调查,并根据调查结果绘制成如图所示的不完整的条形图和扇形图.下列说法正确的是( )
A、 B、 C、 D、4. 用代入法解方程组 时,代入正确的是( )A、x-2-x=4 B、x-2-2x=4 C、x-2+2x=4 D、x-2+x=45. 若 , , 则下列结论正确的是( )A、 B、 C、 D、6. 将点向右平移个单位长度得到点 , 则点所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限7. 若不等式组的解集是 , 则不等式②可以是( )A、 B、 C、 D、8. 我国清代算书《御制数理精蕴》(卷九)中有这样一题:“设如有甲、乙二人人山采果共得三百枚,但云甲数加六百枚,乙数加二百枚,则甲数比乙数多二倍.问甲、乙各得几何.”设甲数为枚,乙数为枚,根据题意可列方程组为( )A、 B、 C、 D、9. 某学校计划在七年级开设折扇、刺绣、剪纸、陶艺四门校本课程,要求每人必须参加,并且只能选择其中一门课程,为了解学生对这四门课程的选择情况,学校从七年级全体学生中随机抽取部分学生进行问卷调查,并根据调查结果绘制成如图所示的不完整的条形图和扇形图.下列说法正确的是( ) A、参加问卷调查的学生人数为名 B、陶艺课程所对应的扇形圆心角的度数是 C、条形图中的剪纸人数为名 D、若该校七年级一共有名学生,则估计选择刺绣课程的学生有名10. 已知关于的不等式组的最小整数解是2,则实数的取值范围是( )A、 B、 C、 D、
A、参加问卷调查的学生人数为名 B、陶艺课程所对应的扇形圆心角的度数是 C、条形图中的剪纸人数为名 D、若该校七年级一共有名学生,则估计选择刺绣课程的学生有名10. 已知关于的不等式组的最小整数解是2,则实数的取值范围是( )A、 B、 C、 D、二、填空题
-
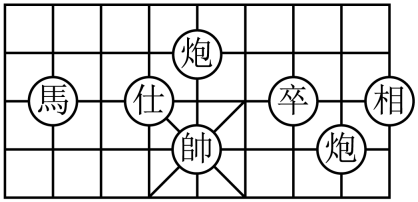
11. 写出一个小于4的正无理数是 .12. “山西,再见!”5月25日,东方甄选山西行专场在山西太原晋祠公园门口告别,此次山西行专场6天带货销售额达亿元,吴宇同学想把这6天每天的销售额占总销售额的百分比用统计图表示出来,则最适宜选用统计图.(填“条形”“扇形”或“折线”)13. 中国象棋有着三千多年的历史,属于二人对抗性游戏的一种,如图是中国象棋的一部分,若棋盘“帥”的位置用表示,“相”的位置用表示,则“馬”的位置表示为 .
 14. 在关于、y的二元一次方程组中,若 , 则a的值为 .15. 某水果超市用每千克元的价格购进千克苹果,经调查在运输和销售过程中质量会损失 , 假设不计超市其他费用,如果超市想要获得及以上的利润,那么这批苹果每千克的售价在进价的基础上应至少提高元.
14. 在关于、y的二元一次方程组中,若 , 则a的值为 .15. 某水果超市用每千克元的价格购进千克苹果,经调查在运输和销售过程中质量会损失 , 假设不计超市其他费用,如果超市想要获得及以上的利润,那么这批苹果每千克的售价在进价的基础上应至少提高元.三、解答题
-
16.(1)、计算:;(2)、解方程组:17. 下面是小明解不等式的过程,请认真阅读并完成任务.
解:去分母,得 . 第一步
去括号,得 . 第二步
移项,得 . 第三步
合并同类项,得 . 第四步
系数化为1,得 . 第五步
(1)、任务一:①以上求解过程中,第一步的依据是 ▲ ;
②以上求解过程中,从第 ▲ 步开始出现错误,错误的原因是 ▲ ;
(2)、任务二:直接写出该不等式的正确解集,并在数轴上表示出来. 18. 已知三角形是由三角形经过平移得到的,它们各顶点在平面直角坐标系中的坐标如下表所示:
18. 已知三角形是由三角形经过平移得到的,它们各顶点在平面直角坐标系中的坐标如下表所示:三角形
三角形
 (1)、观察表中各对应点坐标的变化,并填空: , , ;(2)、在平面直角坐标系中画出三角形及平移后的三角形 .19. 为提高病人免疫力,某医院精选甲、乙两种食物为病人配制营养餐.已知每克甲种食物中铁的含量是蛋白质的2倍,每克乙种食物中铁的含量是蛋白质的 .(1)、设每克甲种食物中含蛋白质x个单位,每克乙种食物中含蛋白质y个单位,请用含x , y的式子填表:
(1)、观察表中各对应点坐标的变化,并填空: , , ;(2)、在平面直角坐标系中画出三角形及平移后的三角形 .19. 为提高病人免疫力,某医院精选甲、乙两种食物为病人配制营养餐.已知每克甲种食物中铁的含量是蛋白质的2倍,每克乙种食物中铁的含量是蛋白质的 .(1)、设每克甲种食物中含蛋白质x个单位,每克乙种食物中含蛋白质y个单位,请用含x , y的式子填表:每克甲种食物
每克乙种食物
蛋白质的含量/单位
x
y
铁的含量/单位
▲
▲
(2)、如果病人每餐需要175个单位的蛋白质和200个单位的铁,每餐需要甲、乙两种食物分别为140克,150克,求每克甲种食物中含蛋白质、铁各多少个单位.20. 山西省自2022年秋季人学的七年级学生开始,信息技术考试采取无纸化上机操作考试.张老师为了解某次考试中本校七年级学生信息技术课程的成绩(满分为100分),随机抽取了50名学生进行统计,并绘制成如图所示的频数分布表和频数分布直方图进行分析.请根据图表提供的信息,解答下列问题: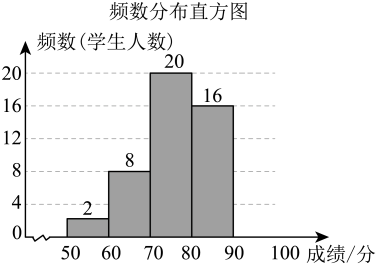
频数分布表
分组
频数
2
8
20
16
a
合计
50
(1)、求频数分布表中a的值.(2)、补全频数分布直方图.(3)、若成绩大于80分为优秀,则这次考试成绩的优秀率是多少?(4)、该校七年级共有600名学生,并全部参加这次考试,请估计成绩超过70分的学生有多少名.21. 如图,已知 .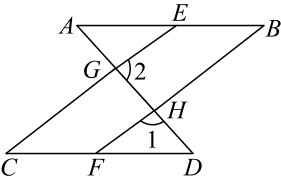 (1)、请判断直线的位置关系,并说明理由;(2)、若 , 求的度数.22. 为切实保障学生安全、便捷出行,某市计划购买甲、乙两种型号的电动公交车共辆,开通“学生公交专线”.已知购买辆甲型公交车和辆乙型公交车需万元,购买辆甲型公交车和辆乙型公交车需万元.(1)、求甲型公交车和乙型公交车每辆各多少万元.(2)、若购买甲型公交车的总费用不高于乙型公交车的总费用,则该市最多可购买多少辆甲型公交车?23. 综合与探究
(1)、请判断直线的位置关系,并说明理由;(2)、若 , 求的度数.22. 为切实保障学生安全、便捷出行,某市计划购买甲、乙两种型号的电动公交车共辆,开通“学生公交专线”.已知购买辆甲型公交车和辆乙型公交车需万元,购买辆甲型公交车和辆乙型公交车需万元.(1)、求甲型公交车和乙型公交车每辆各多少万元.(2)、若购买甲型公交车的总费用不高于乙型公交车的总费用,则该市最多可购买多少辆甲型公交车?23. 综合与探究已知直线 , 直线分别与 , 交于点G , . 将一把含角的直角三角尺按如图1所示的方式放置,使点N , M分别在直线 , 上,且在直线的右侧.
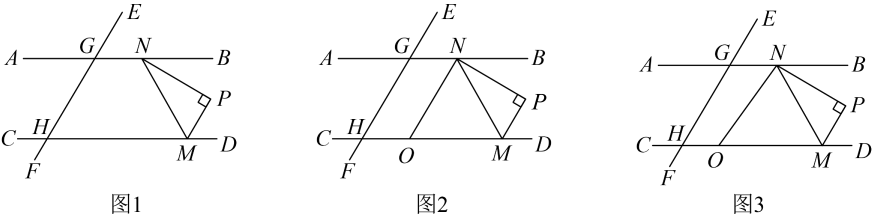 (1)、填空: . (填“”“”或“”)(2)、若的平分线交直线于点O .
(1)、填空: . (填“”“”或“”)(2)、若的平分线交直线于点O .①如图2,当时,求的度数;
②如图3,若将三角尺沿直线向左移动,保持(点N不与点G重合),点N , M分别在直线 , 上,请直接写出和之间的数量关系.