甘肃省白银市2022-2023学年八年级下学期期末数学试题
试卷更新日期:2023-08-18 类型:期末考试
一、单选题
-
1. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 正六边形的内角和为( )A、 B、 C、 D、3. 在中,若 , 则( )A、 B、 C、 D、4. 如图,为测量池塘边A,B两点间的距离,在地面上确定点O,分别取 , 的中点C,D,量得 , 则A,B两点间的距离是( )
2. 正六边形的内角和为( )A、 B、 C、 D、3. 在中,若 , 则( )A、 B、 C、 D、4. 如图,为测量池塘边A,B两点间的距离,在地面上确定点O,分别取 , 的中点C,D,量得 , 则A,B两点间的距离是( )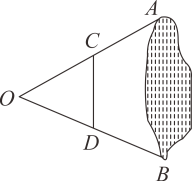 A、3m B、6m C、12m D、24m5. 如图,在中, , D为边的中点,下列结论不一定正确的是( )
A、3m B、6m C、12m D、24m5. 如图,在中, , D为边的中点,下列结论不一定正确的是( ) A、 B、 C、平分 D、6. 下列等式分别是四位同学解方程过程中去分母的一步,其中正确的是( )A、 B、 C、 D、7. 已知 ,则下列不等式中不成立的是( )A、 B、 C、 D、8. 如图,为等边三角形, . 若 , 则( )
A、 B、 C、平分 D、6. 下列等式分别是四位同学解方程过程中去分母的一步,其中正确的是( )A、 B、 C、 D、7. 已知 ,则下列不等式中不成立的是( )A、 B、 C、 D、8. 如图,为等边三角形, . 若 , 则( )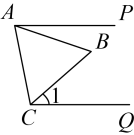 A、 B、 C、 D、9. 如图,直线与相交于点 , 则关于的不等式的解集为( )
A、 B、 C、 D、9. 如图,直线与相交于点 , 则关于的不等式的解集为( ) A、 B、 C、 D、无法确定10. 如图,在中, , , 的垂直平分线交于点E,交于点D,且 , 则的长是( )
A、 B、 C、 D、无法确定10. 如图,在中, , , 的垂直平分线交于点E,交于点D,且 , 则的长是( )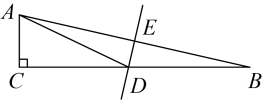 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 若分式 有意义,则 的取值范围是.12. “x的2倍与1的差大于0”用不等式表示为 .13. 将多项式提公因式3xy后,另一个因式为 .14. 如图,将平移后得到 , 连接 . 若 , , 则平移的距离为cm.
 15. 化简分式的结果为 .16. 如图,将AOB绕点O按逆时针方向旋转45°后得到COD,若∠AOB=10°,则∠AOD的度数是 .
15. 化简分式的结果为 .16. 如图,将AOB绕点O按逆时针方向旋转45°后得到COD,若∠AOB=10°,则∠AOD的度数是 . 17. 如图,射线是的平分线,D是射线上一点,于点P, . 若Q是射线上一点, , 则的面积是 .
17. 如图,射线是的平分线,D是射线上一点,于点P, . 若Q是射线上一点, , 则的面积是 .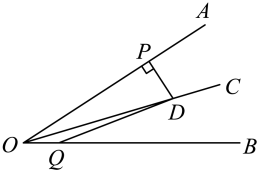 18. 如图,的面积为 , 两对角线相交于点 , 以为邻边作 , 连接 , 交于点;以 , 为邻边作 , 连接 , 交于点;…;依此类推,则的面积为 .
18. 如图,的面积为 , 两对角线相交于点 , 以为邻边作 , 连接 , 交于点;以 , 为邻边作 , 连接 , 交于点;…;依此类推,则的面积为 .
三、解答题
-
19. 化简:20. 分解因式: .21. 解不等式组 , 并将解集表示在所给的数轴上.
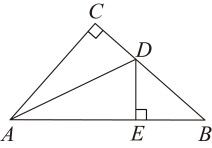
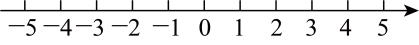 22. 如图,在中, , 平分 , 于 , 若 , , 求的长.
22. 如图,在中, , 平分 , 于 , 若 , , 求的长.
 23. 如图,在四边形中, , , 相交于点分别是的中点,连接 . 求证:四边形是平行四边形.
23. 如图,在四边形中, , , 相交于点分别是的中点,连接 . 求证:四边形是平行四边形.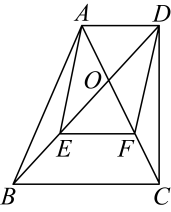 24. 如图,已知的顶点均在由边长为1的正方形组成的网格的格点上.
24. 如图,已知的顶点均在由边长为1的正方形组成的网格的格点上. (1)、画出将先向下平移3格,再向右平移4格后得到的;(2)、画出关于点中心对称的 .25. 如图,佳佳从点出发,前进10米后向右转 , 再前进10米后又向右转 , 如此反复下去,直到他第一次回到出发点 , 他所走的路径构成了一个多边形.
(1)、画出将先向下平移3格,再向右平移4格后得到的;(2)、画出关于点中心对称的 .25. 如图,佳佳从点出发,前进10米后向右转 , 再前进10米后又向右转 , 如此反复下去,直到他第一次回到出发点 , 他所走的路径构成了一个多边形. (1)、佳佳一共走了多少米?(2)、求这个多边形的内角和.26. 如图,在中, , , 于点D,且 .
(1)、佳佳一共走了多少米?(2)、求这个多边形的内角和.26. 如图,在中, , , 于点D,且 . (1)、求的度数;(2)、试判断的形状,并说明理由.27. 如图1,已知点A,B,C,D在一条直线上,BF、CE相交于O,AE=DF,∠E=∠F,OB=OC.
(1)、求的度数;(2)、试判断的形状,并说明理由.27. 如图1,已知点A,B,C,D在一条直线上,BF、CE相交于O,AE=DF,∠E=∠F,OB=OC.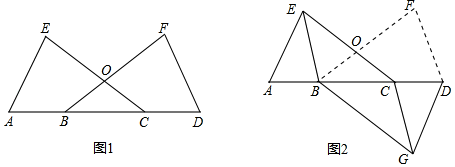 (1)、求证:△ACE≌△DBF;(2)、如果把△DBF沿AD折翻折使点F落在点G,如图2,连接BE和CG. 求证:四边形BGCE是平行四边形.28. “和尚头”是白银区武川乡干旱地区种植的优质小麦之一,其特点是滑润爽口、味感纯正、面筋强、食用方便,是家庭、宾馆、给老人祝寿之佳品.某商店准备用3000元购进两种包装的这种小麦共150袋,已知购买两种小麦的费用相同,且种包装小麦的单价是种包装小麦单价的2倍.(1)、两种包装的小麦单价各是多少?(2)、若计划用不超过4500元的资金再次购进两种包装的小麦共200袋,已知两种包装的单价不变,则种包装的小麦最多能购进多少袋?
(1)、求证:△ACE≌△DBF;(2)、如果把△DBF沿AD折翻折使点F落在点G,如图2,连接BE和CG. 求证:四边形BGCE是平行四边形.28. “和尚头”是白银区武川乡干旱地区种植的优质小麦之一,其特点是滑润爽口、味感纯正、面筋强、食用方便,是家庭、宾馆、给老人祝寿之佳品.某商店准备用3000元购进两种包装的这种小麦共150袋,已知购买两种小麦的费用相同,且种包装小麦的单价是种包装小麦单价的2倍.(1)、两种包装的小麦单价各是多少?(2)、若计划用不超过4500元的资金再次购进两种包装的小麦共200袋,已知两种包装的单价不变,则种包装的小麦最多能购进多少袋?