【备考2024】高考数学（三角函数版块）细点逐一突破训练：任意角与弧度制3

试卷更新日期：2023-08-18 类型：二轮复习

进入出卷网下载

一、选择题

1. 设 $a \in R$ ， $b \in [0, 2 π]$ ．若对任意实数x都有 $\sin (3 x - \frac{π}{3}) =sin (a x + b)$ ，则满足条件的有序实数对（a,b）的对数为（）

A、1 B、2 C、3 D、4

查看试题解析
2. 图 $1$ 中的机械设备叫做“转子发动机”，其核心零部件之一的转子形状是“曲侧面三棱柱”，图2是一个曲侧面三棱柱，它的侧棱垂直于底面，底面是“莱洛三角形”（如图3），莱洛三角形是以正三角形的三个顶点为圆心，正三角形的边长为半径画圆弧得到的，若曲侧面三棱柱的高为4，底面任意两顶点之间的距离为 $10 \sqrt{2}$ ，则其体积为（）

A、 $200 (2 π - 3 \sqrt{3})$ B、 $400 (π - \sqrt{3})$ C、 $40 \sqrt{2} π$ D、 $400 (2 π - \sqrt{3})$

查看试题解析
3. 济南市洪家楼天主教堂于2006年5月被国务院列为全国重点文物保护单位.它是典型的哥特式建筑.哥特式建筑的特点之一就是窗门处使用尖拱造型，其结构是由两段不同圆心的圆弧组成的对称图形.如图2， $\overset{⌢}{A C}$ 和 $\overset{⌢}{B C}$ 所在圆的圆心都在线段AB上，若 $∠ A C B = θ rad$ ， $| A C | = b$ ，则 $\overset{⌢}{A C}$ 的长度为（）

A、 $\frac{θ b}{2 \sin \frac{θ}{2}}$ B、 $\frac{θ b}{2 \cos \frac{θ}{2}}$ C、 $\frac{θ b}{\sin \frac{θ}{2}}$ D、 $\frac{2 θ b}{\cos \frac{θ}{2}}$

查看试题解析
4. 已知一个半径为 $4$ 的扇形圆心角为 $θ (0 < θ < 2 π)$ ，面积为 $2 π$ ，若 $t a n (θ + φ) = 3$ ，则 $t a n φ =$ （）

A、0 B、 $\frac{1}{2}$ C、2 D、 $- \frac{1}{2}$

查看试题解析
5. 平面直角坐标系 $x O y$ 中， $| A B | = 2$ ，该平面上的动线段 $P Q$ 的端点 $P$ 和 $Q$ ，满足 $| \vec{A P} | \leq 5 ， \vec{A P} \cdot \vec{A B} = 6 ， \vec{A Q} = 2 \vec{P A}$ ，则动线段 $P Q$ 所形成图形的面积为（）

A、36 B、60 C、72 D、108

查看试题解析
6. 已知圆锥的底面直径为 $\sqrt{2}$ ，母线长为 $2 \sqrt{2}$ ，则其侧面展开图扇形的圆心角为（）

A、 $\frac{π}{4}$ B、 $\frac{3 π}{4}$ C、 $\frac{π}{2}$ D、 $π$

查看试题解析
7. 为解决皮尺长度不够的问题，实验小组利用自行车来测量A，B两点之间的直线距离.如下图，先将自行车前轮置于点A，前轮上与点A接触的地方标记为点C，然后推着自行车沿AB直线前进（车身始终保持与地面垂直），直到前轮与点B接触.经观测，在前进过程中，前轮上的标记点C与地面接触了10次，当前轮与点B接触时，标记点C在前轮的左上方（以下图为观察视角），且到地面的垂直高度为0.45m.已知前轮的半径为0.3m，则A，B两点之间的距离约为（）（参考数值： $π \approx 3.14$ ）

A、20.10m B、19.94m C、19.63m D、19.47m

查看试题解析
8. 已知圆台形的木桶的上、下底面的半径分别为4和2，木桶的高为 $2 \sqrt{3}$ ，则该木桶的侧面展开成的扇环所对的圆心角为（）

A、 $π$ B、 $\frac{3 π}{4}$ C、 $\frac{2 π}{3}$ D、 $\frac{π}{2}$

查看试题解析
9. 已知扇形的圆心角为120°，半径为3，则这个扇形的面积为（）

A、3π B、2π C、π D、 $\frac{π}{2}$

查看试题解析
10. 埃拉托斯特尼是古希腊亚历山大时期著名的地理学家，他最出名的工作是计算了地球（大圆）的周长：如图，在赛伊尼，夏至那天中午的太阳几乎正在天顶方向（这是从日光直射进该处一井内而得到证明的）.同时在亚历山大城（该处与赛伊尼几乎在同一子午线上），其天顶方向与太阳光线的夹角测得为7.2°.因太阳距离地球很远，故可把太阳光线看成是平行的．已知骆驼一天走100个视距段，从亚历山大城到赛伊尼须走50天．一般认为一个视距段等于157米，则埃拉托斯特尼所测得地球的周长约为（）

A、37680千米 B、39250千米 C、41200千米 D、42192千米

查看试题解析
11. 希波克拉底是古希腊医学家，他被西方尊为“医学之父”，除了医学，他也研究数学.特别是与“月牙形”有关的问题.如图所示.阴影部分的月牙形的边缘都是圆弧，两段圆弧分别是 $△ A B C$ 的外接圆和以 $A B$ 为直径的圆的一部分，若 $∠ A C B = \frac{2 π}{3}$ ， $A C = B C = 1$ ，则该月牙形的面积为（）

A、 $\frac{\sqrt{3}}{4} + \frac{π}{24}$ B、 $\frac{\sqrt{3}}{4} - \frac{π}{24}$ C、 $\frac{1}{4} + \frac{π}{24}$ D、 $\frac{1}{4} - \frac{π}{24}$

查看试题解析
12. 已知圆锥的侧面积是底面积的 $\frac{5}{4}$ 倍，则该圆锥的侧面展开图扇形的圆心角大小为（）

A、 $\frac{4 π}{5}$ B、 $\frac{6 π}{5}$ C、 $\frac{8 π}{5}$ D、 $\frac{9 π}{5}$

查看试题解析
13. 如图， $A$ 是共享单车前轮外边沿上的一点，前轮半径为 $0.25 m$ ，若单车向右行进 $7.33 m$ 时（车轮无滑动），下列描述正确的是 $(π \approx 3.14)$ （）

A、点 $A$ 在前轮的左下位置，距离地面约为 $0.125 m$ B、点 $A$ 在前轮的右下位置，距离地面约为 $0.125 m$ C、点 $A$ 在前轮的左上位置，距离地面约为 $0.375 m$ D、点 $A$ 在前轮的右上位置，距离地面约为 $0.375 m$

查看试题解析
14. 下面正确的是（）

A、 $t a n 1 < s i n 2 < c o s 3$ B、 $s i n 2 < c o s 3 < t a n 1$ C、 $c o s 3 < t a n 1 < s i n 2$ D、 $c o s 3 < s i n 2 < t a n 1$

查看试题解析

二、填空题

15. 已知圆锥展开图的侧面积为2π，且为半圆，则底面半径为．

查看试题解析
16. “一湾如月弦初上，半壁澄波镜比明”描述的是敦煌八景之一的月牙泉.某中学开展暑期社会实践活动，学生通过测量绘制出月牙泉的平面图，如图所示.图中，圆弧 $Q R T$ 是一个以 $O$ 点为圆心､ $Q T$ 为直径的半圆， $Q T = 60 \sqrt{3}$ 米.圆弧 $Q S T$ 的圆心为 $P$ 点， $P Q = 60$ 米，圆弧 $Q R T$ 与圆弧 $Q S T$ 所围成的阴影部分为月牙泉的形状，则该月牙泉的面积为平方米.

查看试题解析
17. 已知弧度数为 $\frac{π}{3}$ 的圆心角所对的弦长为2，则这个圆心角所对的弧长是.

查看试题解析
18. “数摺聚清风，一捻生秋意”是宋代朱翌描写折扇的诗句，折扇出入怀袖，扇骨雕琢，是文人雅士的宠物，如图，这是折扇的示意图，已知D为OA中点，OA＝4， $∠ A O B = \frac{3 π}{4}$ （扇环ABCD）部分的面积是．

查看试题解析
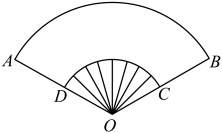19. 设一扇形的周长为 $12$ ，圆心角为 $4$ ，则该扇形的面积为．

查看试题解析
20. $t a n (- 405 °)$ 的值为．

查看试题解析
21. 《乐府诗集》辑有晋诗一组，属清商曲辞吴声歌曲，标题为《子夜四时歌七十五首》.其中《夏歌二十首》的第五首曰：叠扇放床上，企想远风来.轻袖佛华妆，窈窕登高台.诗里的叠扇，就是折扇.一般情况下，折扇可看作是从一个圆面中剪下的扇形制作而成.如图，设扇形的面积为 $S_{1}$ ，其圆心角为 $θ$ ，圆面中剩余部分的面积为 $S_{2}$ ，当 $S_{1}$ 与 $S_{2}$ 的比值为 $\frac{\sqrt{5} - 1}{2}$ 时，扇面为“美观扇面”.若扇面为“美观扇面”，扇形的半径 $R =$ 10，则此时的扇形面积为.

查看试题解析
22. 已知扇形半径为8，弧长为12，则中心角为弧度，扇形面积是

查看试题解析
23. 已知角 $α$ 的顶点与原点重合，始边与x轴正半轴重合，终边过点 $P (- 4 ， 3)$ ，则 $s i n (α + \frac{π}{6}) c o s (α - \frac{π}{6}) =$ .

查看试题解析
24. 炎炎夏日，古代人们乘凉时用的纸叠扇可看作是从一个圆面中剪下的扇形加工制作而成.如图，扇形纸叠扇完全展开后，得到的扇形ABC面积为 $100 π^{2} c m^{2}$ ，则当该纸叠扇的周长最小时， $A B$ 的长度为cm.

查看试题解析
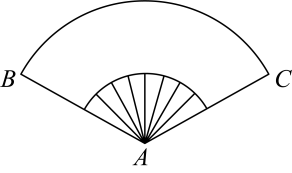25. 一个扇形的弧长和面积都为1，则此扇形的圆心角的弧度数为.

查看试题解析

三、解答题

26. 如图，在平面直角坐标系xOy中，单位圆O与y轴负半轴交于点O'，过点O'作与x轴平行的直线AB，射线O'P从O'A出发，绕着点O'逆时针方向旋转至O'B，在旋转的过程中，记∠AO'P=x（0＜x＜π），O'P所经过的在单位圆O内区域（阴影部分）的面积为S．

(1)、如果 $x = \frac{π}{2}$ ，那么S=；

(2)、关于函数S=f（x）的以下两个结论：
①对任意 $x \in (0 ， \frac{π}{2})$ ，都有 $f (\frac{π}{2} - x) + f (\frac{π}{2} + x) = π$ ；
②对任意x₁ ， x₂∈（0，π），且x₁≠x₂ ，都有 $\frac{f (x_{1}) - f (x_{2})}{x_{1} - x_{2}} < 0$ ．
其中正确的结论的序号是．

查看试题解析
27. 如图，已知OPQ是半径为 $\sqrt{7}$ 圆心角为 $\frac{π}{3}$ 的扇形，C是该扇形弧上的动点，ABCD是扇形的内接矩形，记∠BOC为α．
（Ⅰ）若Rt△CBO的周长为 $\frac{\sqrt{7} (2 \sqrt{10} + 5)}{5}$ ，求 $\frac{3 - c o s 2 α}{c o s^{2} α - s i n α c o s α}$ 的值．
（Ⅱ）求 $\vec{O A} \cdot \vec{A B}$ 的最大值，并求此时α的值．

查看试题解析
28. 某公司拟设计一个扇环形状的花坛（如图所示），该扇环是由以点O为圆心的两个同心圆弧和延长后通过点AD的两条线段围成．设圆弧 $\hat{A B}$ 、 $\hat{C D}$ 所在圆的半径分别为f（x）、R米，圆心角为θ（弧度）．

(1)、若θ= $\frac{π}{3}$ ，r₁=3，r₂=6，求花坛的面积；

(2)、设计时需要考虑花坛边缘（实线部分）的装饰问题，已知直线部分的装饰费用为60元/米，弧线部分的装饰费用为90元/米，预算费用总计1200元，问线段AD的长度为多少时，花坛的面积最大？

查看试题解析
29. AC为对称轴的抛物线的一部分，点B到边AC的距离为2km，另外两边AC，BC的长度分别为8km，2 $\sqrt{5}$ km．现欲在此地块内建一形状为直角梯形DECF的科技园区．

(1)、求此曲边三角形地块的面积；

(2)、求科技园区面积的最大值．

查看试题解析
30. 一扇形的周长为20cm，当扇形的圆心角α等于多少时，这个扇形的面积最大？最大面积是多少？

查看试题解析
31. 如图，某住宅小区的平面图呈圆心角为120°的扇形AOB，小区的两个出入口设置在点A及点C处，且小区里有一条平行于BO的小路CD，已知某人从C沿CD走到D用了10分钟，从D沿DA走到A用了6分钟，若此人步行的速度为每分钟50米，求该扇形的半径OA的长（精确到1米）

查看试题解析
32. 如图：已知扇形MON所在圆半径为1，∠MON= $\frac{π}{2}$ ，扇形内接矩形ABOC，设∠AON=θ．

(1)、将矩形面积S表示为θ的函数，并指出θ的取值范围；

(2)、当θ取何值时，矩形面积S最大，并求S的最大值．

查看试题解析
33. 如图一：球面上的任意两个与球心不在同一条直线上的点和球心确定一个平面，该平面与球相交的图形称为球的大圆，任意两点都可以用大圆上的劣弧进行连接.过球面一点的两个大圆弧，分别在弧所在的两个半圆内作公共直径的垂线，两条垂线的夹角称为这两个弧的夹角.如图二：现给出球面上三个点，其任意两个不与球心共线，将它们两两用大圆上的劣弧连起来的封闭图形称为球面三角形.两点间的弧长定义为球面三角形的边长，两个弧的夹角定义为球面三角形的角.现设图二球面三角形 $A B C$ 的三边长为 $a$ ， $b$ ， $c$ ，三个角大小为 $α$ ， $β$ ， $γ$ ，球的半径为 $R$ .

(1)、求证： $a + b > c$

(2)、①求球面三角形 $A B C$ 的面积 $S$ （用 $α$ ， $β$ ， $γ$ ， $R$ 表示）.
②证明： $α + β + γ > π$ .

查看试题解析
34. 油纸伞是世界上最早的雨伞，是中国古人智慧的结晶.它以手工削制的竹条做伞架，以涂刷天然防水桐油的皮棉纸做伞面.伞面可近似看成圆锥形.若某种油纸伞的伞面下边沿所在圆的半径为 $90 c m$ ，顶点到下边沿上任一点的长度为 $100 c m$ .

(1)、若将该伞的伞面沿一条母线剪开，展开后所得扇形的圆心角为多少弧度？

(2)、若伞面的内外表面需要各刷1次桐油，每平方米需要刷桐油 $\frac{π}{30} k g$ ，则刷一个这样的油纸伞需要多少千克桐油？（参考数据： $π^{2} \approx 9.9$ ）

查看试题解析
35. 已知扇形的周长为30．

(1)、若该扇形的半径为10，求该扇形的圆心角 $α$ ，弧长 $l$ 及面积 $S$ ；

(2)、求该扇形面积 $S$ 的最大值及此时扇形的半径 .

查看试题解析