【备考2024】高考数学（三角函数版块）细点逐一突破训练：任意角与弧度制1

试卷更新日期：2023-08-18 类型：二轮复习

进入出卷网下载

一、选择题

1. 沈括的《梦溪笔谈》是中国古代科技史上的杰作，其中收录了计算圆弧长度的“会圆术”，如图， $\overset{⌢}{A B}$ 是以O为圆心，OA为半径的圆弧，C是AB的中点，D在 $\overset{⌢}{A B}$ 上， $C D ⊥ A B$ ．“会圆术”给出 $\overset{⌢}{A B}$ 的弧长的近似值s的计算公式： $s = A B + \frac{C D^{2}}{O A}$ ．当 $O A = 2 ， ∠ A O B = 60 °$ 时， $s =$ （）

A、 $\frac{11 - 3 \sqrt{3}}{2}$ B、 $\frac{11 - 4 \sqrt{3}}{2}$ C、 $\frac{9 - 3 \sqrt{3}}{2}$ D、 $\frac{9 - 4 \sqrt{3}}{2}$

查看试题解析
2. 如图，在扇形 $A O B$ 中，C是弦 $A B$ 的中点，D在 $\overset{⌢}{A B}$ 上， $C D ⊥ A B$ ．其中 $O A = O B = r$ ， $\overset{⌢}{A B}$ 长为 $l$ $(l < r)$ ．则 $C D$ 的长度约为（提示： $x \in (0 ， \frac{1}{2})$ 时， $c o s x \approx 1 - \frac{x^{2}}{2}$ ）（）

A、 $r - \frac{l^{2}}{8 r}$ B、 $\frac{l^{2}}{8 r}$ C、 $r - \frac{l^{2}}{4 r}$ D、 $\frac{l^{2}}{4 r}$

查看试题解析
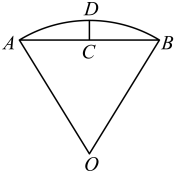3. 勒洛四面体是一个非常神奇的“四面体”，它能在两个平行平面间自由转动，并且始终保持与两平面都接触.勒洛四面体是以正四面体的四个顶点为球心，以正四面体的棱长为半径的四个球的相交部分围成的几何体，若用棱长为4的正四面体 $A B C D$ 作勒洛四面体，如图，则下列说法正确的是（）

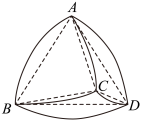A、平面 $A B C$ 截勒洛四面体所得截面的面积为 $8 π - 8 \sqrt{3}$ B、记勒洛四面体上以C，D为球心的两球球面交线为弧 $A B$ ，则其长度为 $\frac{4 π}{3}$ C、该勒洛四面体表面上任意两点间距离的最大值为4 D、该勒洛四面体能够容纳的最大球的半径为 $4 - \sqrt{6}$

查看试题解析
4. 在正三棱柱 $A B C - A_{1} B_{1} C_{1}$ 中， $A B = 2$ ， $A A_{1} = 3$ ，以 $C_{1}$ 为球心， $\frac{\sqrt{39}}{3}$ 为半径的球面与侧面 $A B B_{1} A_{1}$ 的交线长为（）

A、 $\frac{2 \sqrt{3} π}{9}$ B、 $\frac{4 \sqrt{3} π}{9}$ C、 $\frac{2 \sqrt{3} π}{3}$ D、 $\frac{8 \sqrt{3} π}{9}$

查看试题解析
5. 相传早在公元前3世纪，古希腊天文学家厄拉多塞内斯就首次测出了地球半径.厄拉多塞内斯选择在夏至这一天利用同一子午线（经线）的两个城市（赛伊城和亚历山大城）进行观测，当太阳光直射塞伊城某水井 $S$ 时，亚历山大城某处 $A$ 的太阳光线与地面成角 $θ = 82 . 8^{∘}$ ，又知某商队旅行时测得 $A$ 与 $S$ 的距离即劣弧 $\overset{⌢}{A S}$ 的长为5000古希腊里，若圆周率取3.125，则可估计地球半径约为（）

A、35000古希腊里 B、40000古希腊里 C、45000古希腊里 D、50000古希腊里

查看试题解析
6. 如图，圆柱 $O O_{1}$ 的底面半径和母线长均为 $3 ， A B$ 是底面直径，点 $C$ 在圆 $O$ 上且 $O C ⊥ A B$ ，点 $E$ 在母线 $B D 上， B E = 2$ ，点 $F$ 是上底面的一个动点，则（）

A、存在唯一的点 $F$ ，使得 $A F + F E = 2 \sqrt{13}$ B、若 $A E ⊥ C F$ ，则点 $F$ 的轨迹长为4 C、若 $A F ⊥ F E$ ，则四面体 $A C E F$ 的外接球的表面积为 $40 π$ D、若 $A F ⊥ F E$ ，则点 $F$ 的轨迹长为 $2 \sqrt{6} π$

查看试题解析
7. 已知圆锥的顶点为S，高为1，底面圆的直径 $A C = 2 \sqrt{3}$ ， B为圆周上不与A重合的动点，F为线段AB上的动点，则（）

A、圆锥的侧面积为 $2 \sqrt{3} π$ B、 $△ S A B$ 面积的最大值为 $\sqrt{3}$ C、直线SB与平面SAC所成角的最大值为 $\frac{π}{3}$ D、若B是 $\overset{⌢}{A C}$ 的中点，则 $(S F + C F)^{2}$ 的最小值为 $10 + \sqrt{15}$

查看试题解析
8. 已知一个圆锥和圆柱的底面半径和高分别相等，若圆锥的轴截面是等边三角形，则这个圆锥和圆柱的侧面积之比为（）

A、 $\frac{1}{2}$ B、 $\frac{\sqrt{2}}{2}$ C、 $\frac{\sqrt{3}}{3}$ D、 $\sqrt{3}$

查看试题解析
9. 圆锥侧面展开图扇形的圆心角为60°，底面圆的半径为8，则圆锥的侧面积为（）

A、 $384 π$ B、 $392 π$ C、 $398 π$ D、 $404 π$

查看试题解析
10. 某中学开展劳动实习，学生加工制作零件，零件的截面如图（单位： $c m$ ）所示，四边形 $A F E D$ 为矩形， $A B ， C D ， F E$ 均与圆 $O$ 相切， $B ､ C$ 为切点，零件的截面 $B C$ 段为圆 $O$ 的一段弧，已知 $t a n α = \frac{4}{3} ， t a n β = \frac{3}{4}$ ，则该零件的截面的周长为（）cm（结果保留 $π$ ）

A、 $84 + 6 π$ B、 $80 + 5 π$ C、 $75 + 5 π$ D、 $82 + 6 π$

查看试题解析
11. 《几何原本》是古希腊数学家欧几里得的一部不朽之作，书中称轴截面为等腰直角三角形的圆锥为直角圆锥，则直角圆锥侧面展开图的圆心角的弧度数为（）

A、 $\frac{π}{2}$ B、 $\frac{\sqrt{2}}{2} π$ C、 $\sqrt{2} π$ D、 $2 \sqrt{2} π$

查看试题解析
12. 军事上角的度量常用密位制，密位制的单位是“密位”1密位就是圆周的 $\frac{1}{6000}$ 所对的圆心角的大小，.若角 $α = 1000$ 密位，则 $α =$ （）

A、 $\frac{π}{6}$ B、 $\frac{π}{4}$ C、 $\frac{π}{3}$ D、 $\frac{5 π}{12}$

查看试题解析

二、填空题

13. 已知命题 $p ：$ 若 $α ， β$ 为第一象限角，且 $α > β$ ，则 $t a n α > t a n β$ ．能说明p为假命题的一组 $α ， β$ 的值为 $α =$ ， $β =$ ．

查看试题解析
14. “圆材埋壁”是我国古代的数学著作《九章算术》中的一个问题，现有一个“圆材埋壁”的模型，其截面如图所示，若圆柱形材料的底面半径为1，截面圆圆心为 $O$ ，墙壁截面 $A B C D$ 为矩形，且 $A D = 1$ ，则扇形 $O A D$ 的面积是.

查看试题解析
15. 正方形ABCD边长为3，P为正方形ABCD边界及内部的动点，且 $| P B | = 2 | P A |$ ，则动点P的轨迹长度为．

查看试题解析
16. 已知圆锥的母线长为3，其侧面展开图是一个圆心角为 $\frac{2 π}{3}$ 的扇形，则该圆锥的底面半径为.

查看试题解析
17. 写出两个与 $- \frac{11}{3} π$ 终边相同的角．

查看试题解析
18. 变径圆弧螺旋线是以不同半径的圆弧连接而成的螺旋线，这种螺旋线极具美感.图1是鹦鹉螺的截面，其轮廓是等比变径螺旋线（半径构成等比数列），图2是一段等差变径圆弧螺旋线（半径构成等差数列），其中ABCDEF是边长为1的正六边形，弧 $F A_{1}$ 是以A为圆心，AF为半径的圆弧，弧 $A_{1} B_{1}$ 是以B为圆心， $B B_{1}$ 为半径的圆弧，弧 $B_{1} C_{1}$ 是以C为圆心， $C C_{1}$ 为半径的圆弧，依次类推，已知各圆弧的圆心角均等于正六边形的外角，则弧 $E_{1} F_{1}$ 的长为.

查看试题解析
19. 已知正三棱锥 $P - A B C$ 内接于半径为2的球 $O$ ，且扇形 $O P A$ 的面积为 $\frac{4 π}{3}$ ，则正三棱锥 $P - A B C$ 的体积为．

查看试题解析
20. 《九章算术》是中国古代的数学名著，其中《方田》一章给出了弧田（由圆弧和其所对弦所围成）面积的计算公式：弧田面积 $= \frac{1}{2}$ （弦 $\times$ 矢 $+$ 矢 $^{2}$ ）．公式中“弦”指圆弧所对弦长，“矢”等于圆弧的最高点到弦的距离．如图，弧田是由圆弧 $\overset{⌢}{A B}$ 和其所对弦 $A B$ 围成的图形，若弧田的弧 $\overset{⌢}{A B}$ 长为 $\frac{8 π}{3}$ ，弧所在的圆的半径为4，则利用九章算术中的弧田面积公式计算出来的面积与实际面积之差为．

查看试题解析
21. “一湾如月弦初上，半壁澄波镜比明”描述的是敦煌八景之一的月牙泉.如图所示，月牙泉由两段在同一平面内的圆弧形岸连接围成.两岸连接点间距离为 $60 \sqrt{3}$ 米.其中外岸为半圆形，内岸圆弧所在圆的半径为60米.某游客绕着月牙泉的岸边步行一周，则该游客步行的路程为米.

查看试题解析
22. 下图为某月牙潭的示意图，该月牙潭是由两段在同一平面内的圆弧形堤岸连接围成，其中外堤岸为半圆形，内堤岸圆弧所在圆的半径为30米，两堤岸的连接点A，B间的距离为 $30 \sqrt{2}$ 米，则该月牙潭的面积为平方米．

查看试题解析
23. 已知三棱锥 $P - A B C$ 中， $A P$ 、 $A B$ 、 $A C$ 三条棱两两垂直，且长度均为 $2 \sqrt{3}$ ，以顶点 $P$ 为球心，4为半径作一个球，则该球面被三棱锥四个表面截得的所有弧长之和为．

查看试题解析

三、解答题

24. 在极坐标系中，曲线 $C ： ρ = 4 \cos θ$ ，以极点O为旋转中心，将曲线C逆时针旋转 $\frac{π}{3}$ 得到曲线 $C^{'}$ .

（Ⅰ）求曲线 $C^{'}$ 的极坐标方程；

（Ⅱ）求曲线C与曲线 $C^{'}$ 的公共部分面积.

查看试题解析
25. 如图，一个圆心角为直角的扇形AOB 花草房，半径为1，点P 是花草房弧上一个动点，不含端点，现打算在扇形BOP 内种花，PQ⊥OA，垂足为Q，PQ 将扇形AOP
分成左右两部分，在PQ 左侧部分三角形POQ 为观赏区，在PQ 右侧部分种草，已知种花的单位面积的造价为3a，种草的单位面积的造价为2a，其中a 为正常数，设∠AOP=θ，种花的造价与种草的造价的和称为总造价，不计观赏区的造价，设总造价为f（θ）

(1)、求f（θ）关于θ 的函数关系式；

(2)、求当θ 为何值时，总造价最小，并求出最小值．

查看试题解析
26. 从① $s i n α + c o s α = \frac{\sqrt{2}}{2}$ ， ② $s i n α - c o s α = \frac{\sqrt{6}}{2}$ ， ③ $t a n (2 π + α) = \sqrt{3} - 2$ ，三个条件中选择一个，补充在下面的问题中，再回答后面两个小问．
已知 $0 < α < π$ ，且满足____．

(1)、判断 $α$ 是第几象限角；

(2)、求值： $s i n^{2} α - 3 s i n α c o s α$ ．

查看试题解析
27. 如图，在直角 $△ A O B$ 中， $∠ O A B = \frac{π}{6}$ ，斜边 $A B = 8$ ， $D$ 是 $A B$ 中点，现将直角 $△ A O B$ 以直角边 $A O$ 为轴旋转一周得到一个圆锥.点 $C$ 为圆锥底面圆周上一点，且 $∠ B O C = \frac{π}{2}$ .

(1)、求圆锥的体积与侧面积；

(2)、求直线 $C D$ 与平面 $B O C$ 所成的角的正切值.

查看试题解析
28. 中国传统折扇文化有着极其深厚的底蕴，一般情况下，折扇可看作是由从一个圆面中剪下的扇形制作而成.设制作扇子的扇形面积为 $S_{1}$ ，圆面中剩下部分的面积为 $S_{2}$ ，当 $\frac{S_{1}}{S_{2}} = \frac{\sqrt{5} - 1}{2} \approx 0.618$ 时，扇面看上去形状较为美观.那么，此时制作扇子的扇形圆心角约为（）

A、 $π$ B、 $\frac{5 π}{6}$ C、 $\frac{3 π}{4}$ D、 $\frac{2 π}{3}$

查看试题解析
29. 已知扇形的圆心角是 $α$ ，半径为 $r$ ，弧长为 $l$ .

(1)、若 $α = 13 5^{∘}$ ， $r = 10$ ，求扇形的弧长 $l$ ；

(2)、若扇形 $A O B$ 的周长为 $22$ ，当扇形的圆心角 $α$ 为多少弧度时，这个扇形的面积最大，并求出此时扇形面积的最大值.

查看试题解析
30. 如图，在扇形 $O P Q$ 中，半径 $O P = 2$ ，圆心角 $∠ P O Q = \frac{π}{3}$ ，B是扇形弧上的动点，矩形 $A B C D$ 内接于扇形．记 $∠ B O C = α$ ，求当角 $α$ 取何值时，矩形 $A B C D$ 的面积最大？并求出这个最大值．

查看试题解析
31. 已知扇形 $A O B$ 的圆心角为 $\frac{2 π}{3}$ ， $A B = 2 \sqrt{3}$ .

(1)、求扇形 $A O B$ 的弧长；

(2)、求图中阴影部分的面积.

查看试题解析
32. 如图，在扇形OAB中，半径OA=1，圆心角 $∠ A O B = \frac{π}{3} ，$ C是扇形弧上的动点，矩形CDEF内接于扇形，且OE=OF.记∠AOC=θ，求当角θ为何值时，矩形CDEF的面积S最大?并求出这个最大的面积.

查看试题解析
33. 已知扇形的面积为 $\frac{π}{6}$ ，弧长为 $\frac{π}{6}$ ，设其圆心角为 $α$

(1)、求 $α$ 的弧度；

(2)、求 $\frac{\cos (\frac{π}{2} + α) \sin (- π - α)}{\cos (\frac{11 π}{2} - α) \sin (\frac{9 π}{2} + α)}$ 的值.

查看试题解析
34. 如图所示，摩天轮的半径为 $50 m$ ，最高点距离地面高度为 $110 m$ ，摩天轮的圆周上均匀地安装着24个座舱，并且运行时按逆时针匀速旋转，转一周大约需要 $12 \min$ .甲，乙两游客分别坐在 $P$ ， $Q$ 两个座舱里，且他们之间间隔2个座舱(本题中将座舱视为圆周上的点).

(1)、求劣弧 $P Q$ 的弧长 $l$ (单位： $m$ )；

(2)、设游客丙从最低点 $M$ 处进舱，开始转动 $t \min$ 后距离地面的高度为 $H m$ ，求在转动一周的过程中， $H$ 关于时间 $t$ 的函数解析式；

(3)、若游客在距离地面至少 $85 m$ 的高度能够获得最佳视觉效果，请问摩天轮转动一周能有多长时间使甲，乙两位游客都有最佳视觉效果.

查看试题解析
35. 已知角 $α = - 920 °$ .
（Ⅰ）把角 $α$ 写成 $2 k π + β$ （ $0 \leq β < 2 π, k \in Z$ ）的形式，并确定角 $α$ 所在的象限；

（Ⅱ）若角 $γ$ 与 $α$ 的终边相同，且 $γ \in (- 4 π, - 3 π)$ ，求角 $γ$ .

查看试题解析