【备考2024】高考数学(函数版块)细点逐一突破训练:函数的应用
试卷更新日期:2023-08-17 类型:二轮复习
一、选择题
-
1. 已知函数 的定义域均为R,且 .若 的图像关于直线 对称, ,则 ( )A、-21 B、-22 C、-23 D、-242. 已知函数 ,则对任意实数 ,有( )A、 B、 C、 D、3. 某商场要将单价分别为36元 , 48元 , 72元的3种糖果按3:2:1的比例混合销售,其中混合糖果中每一颗糖果的质量都相等.那么该商场对混合糖果比较合理的定价应为( )A、52元 B、50元 C、48元 D、46元4. 2021年5月15日7时18分,天问一号探测器成功着陆于火星乌托邦平原南部预选着陆区,我国首次火星探测任务着陆火星取得成功,航天技术得以发展,得益于如下的齐奥尔科大斯基公式: , 其中 , 分别为燃料燃烧前与燃烧后的火箭质量,是燃料喷出的速度,是火箭的初速度,是燃料完全燃尽时火箭的速度,现准备发射一个二级火箭(初速度),每级火箭的箭体结构的质量均为50吨,每级火箭携带的燃料质量均为250吨,燃料喷出的速度为 , 先点燃第一级火箭燃料,燃料燃尽后,第一级火箭自动脱离,同时点燃第二级火箭的燃料,则当第二级火箭的燃料燃尽时,火箭的速度约为( )(参考数据: , )A、 B、 C、 D、5. 有这样一种说法:一张纸经过一定次数对折之后厚度能超过地月距离.但实际上,因为纸张本身有厚度,我们并不能将纸张无限次对折,当厚度超过纸张的长边时,便不能继续对折了,一张长边为 , 厚度为的矩形纸张沿两个方向不断对折,则经过两次对折,长边变为 , 厚度变为.在理想情况下,对折次数满足关系: , 根据以上信息,一张长为40cm,厚度为0.1的纸经过对折后的厚度的最大值约为( )()A、1.28cm B、2.56cm C、12.8cm D、25.6cm6. 已知定义在R上的函数 满足:(1) ;(2) 为奇函数;(3)当 时, 图象连续且 恒成立,则 的大小关系正确的为( )A、
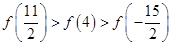 B、
B、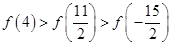 C、
C、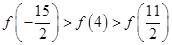 D、
D、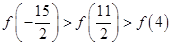 7. 已知函数 与 的图象上存在关于 轴对称的点,则 的取值范围是( )
7. 已知函数 与 的图象上存在关于 轴对称的点,则 的取值范围是( )
A、 B、 C、 D、8. 酒驾是严重危害交通安全的违法行为.根据国家有关规定:驾驶人血液中的酒精含量大于(或等于)毫克/毫升,小于毫克/毫升的情况下驾驶机动车属于饮酒驾车;含量大于(或等于)毫克/毫升的情况下驾驶机动车属于醉酒驾车.假设某驾驶员一天晚上点钟喝了一定量的酒后,其血液中酒精含量上升到毫克/毫升.如果在停止喝酒后,他血液中酒精含量以每小时的速度减少,则他次日上午最早( )点(结果取整数)开车才不构成酒驾.(参考数据: , )A、 B、 C、 D、9. 对于一个函数 , 若存在两条距离为的直线和 , 使得在时恒成立,称函数在D内有一个宽度为的通道.则下列函数在内有一个宽度小于等于的通道的有( )A、 B、 C、(表示不超过的最大整数) D、10. 如图 是某条公共汽车线路收支差额 与乘客量 的图象(收支差额 车票收入 支出费用).由于目前本条线路亏损,公司有关人员将图 变为图 与图 ,从而提出了扭亏为盈的两种建议.下面有 种说法: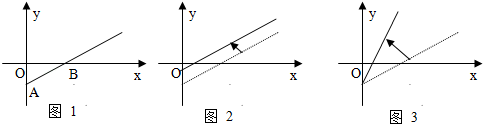
⑴图 的建议是:减少支出,提高票价;(2)图 的建议是:减少支出,票价不变;(3)图 的建议是:减少支出,提高票价;(4)图 的建议是:支出不变,提高票价;上面说法中正确的是( )
A、(1)(3) B、(1)(4) C、(2)(4) D、(2)(3)11. 对于任意实数x,符号[x]表示x的整数部分,即[x]是不超过x的最大整数,例[2]=2;[2.1]=2;[-2.2]=-3, 这个函数[x]叫做“取整函数”,它在数学本身和生产实践中有广泛的应用。那么 的值为( )A、21 B、76 C、264 D、64212. 已知函数 是定义在 上的偶函数,且对任意的 ,当 ,若直线 与函数 的图像在 内恰有两个不同的公共点,则实数 的值是( )A、0 B、0或 C、 或 D、0或13. 若(其中a为整数,),则把整数a叫做离实数x最近的整数,并用符号“”表示“离实数x最近的整数为a”.设函数 , 下列结论正确的为( )A、 B、 C、函数为偶函数且其值域为 D、函数图象的对称轴方程为二、填空题
-
14. 某超市在“五一”活动期间,推出如下线上购物优惠方案:一次性购物在99元(含99元)以内,不享受优惠;一次性购物在99元(不含99元)以上,299元(含299元)以内,一律享受九折优惠;一次性购物在299元(不含299元)以上,一律享受八折优惠;小敏和小昭在该超市购物,分别挑选了原价为70元和280元的商品,如果两人把商品合并由小昭一次性付款,并把合并支付比他们分别支付节省的钱,按照两人购买商品原价的比例分配,则小敏需要给小昭元.15. 数学中有许多形状优美、寓意美好的曲线,如图:四叶草曲线 就是其中一种,其方程为 .给出下列四个结论:
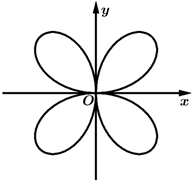
①曲线C有四条对称轴;
②曲线C上的点到原点的最大距离为 ;
③在第一象限内,过曲线C上一点作两坐标轴的垂线与两坐标轴围成的矩形面积的最大值为 ;
④四叶草面积小于 .
其中,所有正确结论的序号是.
16. 规定记号" "表示一种运算,即 ,若 ,函数 的图象关于直线 对称,则 .17. 某人的月工资由基础工资和绩效工资组成2010年每月的基础工资为2100元、绩效工资为2000元从2011年起每月基础工资比上一年增加210元、绩效工资为上一年的 照此推算,此人2019年的年薪为万元(结果精确到 )18. 已知函数 .若 … ,则满足 的 的值为 .19. 如图放置的边长为1的正方形 沿 轴滚动,点 恰好经过原点.设顶点 的轨迹方程是 ,则对函数 有下列判断:①函数 是偶函数;②对任意的 ,都有 ;③函数 在区间 上单调递减;④函数 的值域是 ;⑤ .其中判断正确的序号是 .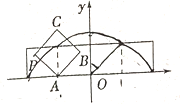 20. 已知函数 , ,其中 .若满足不等 的解的最小值为 ,则实数 的取值范围是.
20. 已知函数 , ,其中 .若满足不等 的解的最小值为 ,则实数 的取值范围是.
21. 已知函数在上有定义,若对 , 都有 , 则称在上具有性质.给出下列四个结论:①在上具有性质;
②在上具有性质;
③若函数在上具有性质且在处取得最大值 , 则对 , 都有;
④若函数在上具有性质 , 对 , 都有.
其中所有正确结论的序号是.
22. 某市出租车的计价标准为1.2元 , 起步价为6元,即最初(不含)计费6元.若某人乘坐该市的出租车去往处的目的地,且一路畅通,等候时间为0,那么他需要支付的车费为.23. 高斯是德国著名的数学家,近代数学奠基者之一,享有“数学王子”的称号,为了纪念数学家高斯,人们把函数称为高斯函数,其中表示不超过x的最大整数,设 , 则满足方程的所有解之和为.24. 某地方政府为鼓励全民创业,拟对本地年产值(单位:万元)的小微企业进行奖励,奖励方案为:奖金y(单位:万元)随企业年产值x的增加而增加,且奖金不低于8万元,同时奖金不超过企业年产值的12%.若函数 , 则实数的取值范围为.三、解答题
-
25. 对于两个定义域相同的函数和 , 若存在实数m、n使 , 则称函数是由“基函数和”生成的.(1)、若和生成一个偶函数 , 求的值;(2)、若由函数( , 且)生成,求的取值范围:(3)、试利用“基函数和”生成一个函数 , 使之满足下列条件:①是偶函数;②有最小值1.求函数的解析式并进一步研究该函数的单调性.(无需证明)26. 已知甲、乙两名工人在同样条件下每天各生产100件产品,且每生产1件正品可获利20元,生产1件次品损失30元,甲,乙两名工人100天中出现次品件数的情况如表所示.
甲每天生产的次品数/件
0
1
2
3
4
对应的天数/天
40
20
20
10
10
乙每天生产的次品数/件
0
1
2
3
对应的天数/天
30
25
25
20
(1)、将甲每天生产的次品数记为 (单位:件),日利润记为 (单位:元),写出 与 的函数关系式;(2)、如果将统计的100天中产生次品量的频率作为概率,记 表示甲、乙两名工人1天中各自日利润不少于1950元的人数之和,求随机变量 的分布列和数学期望.27. 已知函数 , , .(1)、当时,求函数的单调区间;(2)、设函数的最小值为 , 求函数的最小值.(其中是自然对数的底数)
28. 用水清洗果蔬上残留的农药.对用一定量的水清洗一次的效果做如下假定:用1个单位量的水可以洗掉果蔬上残留农药的一半,用水越多洗掉的农药量也越多,但总还有农药残留在果蔬上.设用单位量的水清洗一次以后,果蔬上残留的农药量与本次清洗前残留的农药的农药量的比值为函数.(1)、试规定的值,并解释其实际意义.(2)、试根据假定写出函数应该满足的条件或性质(三条).(3)、设 , 现有单位量的水,可以清洗一次,也可以把水平均分成2份后清洗两次,试问:用那种方案清洗后果蔬上残留的农药比较少?说明理由.29. 为了印刷服务上一个新台阶,学校打印社花费5万元购进了一套先进印刷设备,该设备每年的管理费是0.45万元,使用年时,总的维修费用为万元,问:(1)、设年平均费用为y万元,写出y关于x的表达式;(年平均费用=)(2)、这套设备最多使用多少年报废合适?(即使用多少年的年平均费用最少)30. 用水清洗一堆蔬菜上的农药,设用个单位量的水清洗一次以后,蔬菜上残留的农药量与本次清洗前残留的农药量之比为 , 且已知用1个单位量的水清洗一次,可洗掉本次清洗前残留农药量的 , 用水越多洗掉的农药量也越多,但总还有农药残留在蔬菜上.(1)、根据题意,直接写出函数应该满足的条件和具有的性质;(2)、设 , 现用()个单位量的水可以清洗一次,也可以把水平均分成份后清洗两次,问用哪种方案清洗后蔬菜上残留的农药量比较少,说明理由;(3)、若满足题意,直接写出一组参数的值.31. 某地需要修建一条大型输油管道通过240公里宽的沙漠地带,该段输油管道两端的输油站已建好,余下工程是在该段两端已建好的输油站之间铺设输油管道和等距离修建增压站(又称泵站).经预算,修建一个增压站的工程费用为400万元,铺设距离为公里的相邻两增压站之间的输油管道费用为万元.设余下工程的总费用为万元.(1)、试将表示成的函数;(2)、需要修建多少个增压站才能使最小,其最小值为多少?32. 已知函数 .(1)、求不等式 的解集;(2)、若不等式 对于 恒成立,求实数 的取值范围.33. 已知某手机品牌公司生产某款手机的年固定成本为40万元,每生产1万部还需另投入16万元,设公司一年内共生产该手机 万部并全部销售完,每万部的销售收入为 万元,且(1)、写出年利润 (万元)关于年产量 (万部)的函数解析式;(2)、当年产量为多少万部时,公司在该款手机的生产中所获得的利润最大?并求出最大利润.34. 已知某电子公司生产某款手机的年固定成本为40万美元,每生产1万部还需另投入16万美元,设该公司一年内共生产该款手机万部并全部销售完,每万部的销售收入为万美元,且(1)、写出年利润(万美元)关于年产量(万部)的函数解析式(利润=销售收入成本);(2)、当年产量为多少万部时,该公司在该款手机的生产中所获得的利润最大?并求出最大利润.35. 某工厂生产某种产品的年固定成本为200万元,每生产 千件,需另投入成本 万元,当年产量不足50千件时, ,当年产量不小于50千件时, ,已知每千件商品售价为50万元,通过市场分析,该厂生产的商品能全部售完.(1)、写出年利润 (万元)关于年产量 (千件)的函数解析式;(2)、当年产量为多少千件时,该厂在这一商品的生产中所获利润最大?