【备考2024】高考数学(函数版块)细点逐一突破训练:对数函数4
试卷更新日期:2023-08-17 类型:二轮复习
一、选择题
-
1. 已知 , , , 则( )A、 B、 C、 D、2. 已知 ,则( )A、 B、 C、 D、3. 已知 ,则下列判断正确的是( )A、 B、 C、 D、4. 下列函数中最小值为4的是( )A、 B、 C、 D、5. 设 , , ,则( )A、a<b<c B、b<c<a C、b<a<c D、c<a<b6. 已知 , , , 则有( )A、 B、 C、 D、7. 若实数、满足 , 则下列不等式中成立的是( )A、 B、 C、 D、8. 函数是( )A、奇函数 B、偶函数 C、奇函数也是偶函数 D、非奇非偶函数9. 函数的图像是( )A、
 B、
B、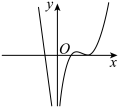 C、
C、 D、
D、 10. 已知集合 , 则( )A、 B、 C、 D、11. 已知函数在上单调递减,则实数的取值范围( )A、 B、 C、 D、12. 已知 , , , 则( )A、 B、 C、 D、13. 函数的图像与函数的图像的交点个数为( )A、2 B、3 C、4 D、014. 已知函数 , 则不等式的解集为( )A、 B、 C、 D、15. “”是“”的( )A、充分而不必要条件 B、必要而不充分条件 C、充分必要条件 D、既不充分也不必要条件
10. 已知集合 , 则( )A、 B、 C、 D、11. 已知函数在上单调递减,则实数的取值范围( )A、 B、 C、 D、12. 已知 , , , 则( )A、 B、 C、 D、13. 函数的图像与函数的图像的交点个数为( )A、2 B、3 C、4 D、014. 已知函数 , 则不等式的解集为( )A、 B、 C、 D、15. “”是“”的( )A、充分而不必要条件 B、必要而不充分条件 C、充分必要条件 D、既不充分也不必要条件二、填空题
-
16. 对任意正实数 , 记函数在上的最小值为 , 函数在上的最大值为 , 若 , 则的所有可能值.17. 如图,某荷塘里浮萍的面积y(单位:)与时间t(单位:月)满足关系式:(a为常数),记().给出下列四个结论:

①设 , 则数列是等比数列;
②存在唯一的实数 , 使得成立,其中是的导函数;
③常数;
④记浮萍蔓延到 , , 所经过的时间分别为 , , , 则 .
其中所有正确结论的序号是 .
18. 写出一个同时具有下列四个性质的函数 .①定义域为 ;②单调递增;③ ;④ .19. 不等式 的解集是.20. 已知函数 是 的递减函数,则实数 的取值范围是.21. 若函数 满足:(1)对于任意实数 ,当 时,都有 ;(2) ,则 .(答案不唯一,写出满足这些条件的一个函数即可)22. 若 克不饱和糖水中含有 克糖,则糖的质量分数为 ,这个质量分数决定了糖水的甜度.如果在此糖水中再添加 克糖,生活经验告诉我们糖水会变甜,从而可抽象出不等式 ( , )数学中常称其为糖水不等式.依据糖水不等式可得出 (用“ ”或“ ”填空);并写出上述结论所对应的一个糖水不等式.23. 已知函数 ,若方程 有两个根,则实数m的取值范围为 .24. 函数 的值域为.25. 已知 ,则a+b. (填“>”或“=”或“<”).三、解答题
-
26. 已知为等比数列, , , 分别是下表第一、二、三行中的数,且 , , 中的任何两个数都不在下表的同一列,为等差数列,其前项和为 , 且 , .
第一列
第二列
第三列
第一行
1
5
2
第二行
4
3
10
第三行
9
8
20
(1)、求数列 , 的通项公式;(2)、若 , 其中是高斯函数,表示不超过的最大整数,如 , , 求数列的前100项的和 .27. 已知(其中且).(1)、若 , , 求实数的取值范围;(2)、若 , 的最大值大于1,求的取值范围.28. 设函数 的反函数为 , .(1)、若 ,求 的取值范围 ;(2)、在(1)的条件下,设 ,当 时,函数 的图像与直线 有公共点,求实数 的取值范围.29. 若函数 的定义域不是 ,求实数 的取值范围.30. 已知 对 函数 总有意义, 函数 在 上是增函数;若命题“ ”为真,“ ”为假,求 的取值范围.
31. 已知函数f(x)=log2(3+x)﹣log2(3﹣x),(1)、求函数f(x)的定义域,并判断函数f(x)的奇偶性;(2)、已知f(sinα)=1,求α的值.32. 已知函数 (a>0,a≠1)是奇函数.(1)、求实数m的值;(2)、判断函数f(x)在(1,+∞)上的单调性,并给出证明;(3)、当x∈(n,a﹣2)时,函数f(x)的值域是(1,+∞),求实数a与n的值.解:33. 已知函数 (a>0,a≠1)是奇函数.(1)、求实数m的值;(2)、判断函数f(x)在(1,+∞)上的单调性,并给出证明;(3)、当x∈(n,a﹣2)时,函数f(x)的值域是(1,+∞),求实数a与n的值.