【备考2024】高考数学(函数版块)细点逐一突破训练:对数函数2
试卷更新日期:2023-08-17 类型:二轮复习
一、选择题
-
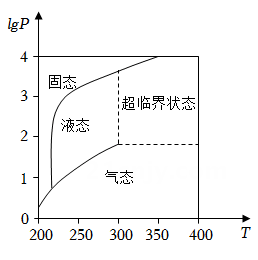
1. 在北京冬奥会上,国家速滑馆“冰丝带”使用高效环保的二氧化碳跨临界直冷制冰技术,为实现绿色冬奥作出了贡献,如图描述了一定条件下二氧化碳所处的状态与 和 的关系,其中 表示温度,单位是 ; 表示压强,单位是bar,下列结论中正确的是( )
 A、当 , 时,二氧化碳处于液态 B、当 , 时,二氧化碳处于气态 C、当 , 时,二氧化碳处于超临界状态 D、当 , 时,二氧化碳处于超临界状态2. 青少年视力是社会普遍关注的问题,视力情况可借助视力表测量,通常用五分记录法和小数记录法记录视力数据,五分记录法的数据L和小数记数法的数据V满足L=5+lgV。已知某同学视力的五分记录法的数据为4.9,则其视力的小数记数法的数据约为( )( ≈1.259)A、1.5 B、1.2 C、0.8 D、0.63. 若 ,则 ( )A、-1 B、 C、1 D、4. 设a=log32,b=log53,c= ,则( )A、a<c<b B、a<b<c C、b<c<a D、c<a<b5. 若 , 则( )A、是等差数列 B、是等比数列 C、是等差数列 D、是等比数列6. 已知 , , , 试比较a,b,c的大小关系为( )A、 B、 C、 D、7. 已知 , , 则( )A、 B、 C、 D、8. 2020年12月17日凌晨1时59分,嫦娥五号返回器携带月球样品成功着陆,这是我国首次实现了地外天体采样返回,标志着中国航天向前又迈出了一大步.月球距离地球约38万千米,有人说:在理想状态下,若将一张厚度约为0.1毫米的纸对折次其厚度就可以超过到达月球的距离,那么至少对折的次数是( )( , )A、40 B、41 C、42 D、439. 溶液酸碱度是通过计量的,的计算公式为 , 其中表示溶液中氢离子的浓度,单位是摩尔/升.已知某溶液的值为2.921,则该溶液中氢离子的浓度约为( )(取 , )A、摩尔/升 B、摩尔/升 C、摩尔/升 D、摩尔/升10. 若 , , , 则关于a、b、c的大小关系,下列说法正确的是( )A、 B、 C、 D、11. 香农-威纳指数()是生态学中衡量群落中生物多样性的一个指数,其计算公式是 , 其中是该群落中生物的种数,为第个物种在群落中的比例,下表为某个只有甲、乙、丙三个种群的群落中各种群个体数量统计表,根据表中数据,该群落的香农-威纳指数值为( )
A、当 , 时,二氧化碳处于液态 B、当 , 时,二氧化碳处于气态 C、当 , 时,二氧化碳处于超临界状态 D、当 , 时,二氧化碳处于超临界状态2. 青少年视力是社会普遍关注的问题,视力情况可借助视力表测量,通常用五分记录法和小数记录法记录视力数据,五分记录法的数据L和小数记数法的数据V满足L=5+lgV。已知某同学视力的五分记录法的数据为4.9,则其视力的小数记数法的数据约为( )( ≈1.259)A、1.5 B、1.2 C、0.8 D、0.63. 若 ,则 ( )A、-1 B、 C、1 D、4. 设a=log32,b=log53,c= ,则( )A、a<c<b B、a<b<c C、b<c<a D、c<a<b5. 若 , 则( )A、是等差数列 B、是等比数列 C、是等差数列 D、是等比数列6. 已知 , , , 试比较a,b,c的大小关系为( )A、 B、 C、 D、7. 已知 , , 则( )A、 B、 C、 D、8. 2020年12月17日凌晨1时59分,嫦娥五号返回器携带月球样品成功着陆,这是我国首次实现了地外天体采样返回,标志着中国航天向前又迈出了一大步.月球距离地球约38万千米,有人说:在理想状态下,若将一张厚度约为0.1毫米的纸对折次其厚度就可以超过到达月球的距离,那么至少对折的次数是( )( , )A、40 B、41 C、42 D、439. 溶液酸碱度是通过计量的,的计算公式为 , 其中表示溶液中氢离子的浓度,单位是摩尔/升.已知某溶液的值为2.921,则该溶液中氢离子的浓度约为( )(取 , )A、摩尔/升 B、摩尔/升 C、摩尔/升 D、摩尔/升10. 若 , , , 则关于a、b、c的大小关系,下列说法正确的是( )A、 B、 C、 D、11. 香农-威纳指数()是生态学中衡量群落中生物多样性的一个指数,其计算公式是 , 其中是该群落中生物的种数,为第个物种在群落中的比例,下表为某个只有甲、乙、丙三个种群的群落中各种群个体数量统计表,根据表中数据,该群落的香农-威纳指数值为( )物种
甲
乙
丙
合计
个体数量
A、 B、 C、 D、12. 已知数列是首项为的正项等比数列,若A,B,C是直线l上不同的三点,O为平面内任意一点,且 , 则( )A、 B、数列的前6项和为 C、数列是递减的等差数列 D、若 , 则数列的前n项和的最大值为113. 已知 , 且 , 则下列不等关系成立的是( )A、 B、 C、 D、14. 已知 , , , 则下列判断正确的是( )A、 B、 C、 D、二、填空题
-
15. 计算: .16. 已知函数 , , 若 , , 使得 , 则 .17. 已知函数 ,则 的值为 .18. .19. 某牧场2022年年初牛的存栏数为1200,计划以后每年存栏数的增长率为20%,且在每年年底卖出100头牛,按照该计划预计年初的存栏量首次超过8900头.(参考数据: , )20. 某射手每次射击击中目标的概率均为0.6,该名射手至少需要射击次才能使目标被击中的概率超过0.999,(参考数据: , )21. 在如今这个5G时代,6G研究己方兴末艾,2021年8月30日第九届未来信息通信技术国际研讨会在北京举办,会上传出消息,未来6G速率有望达到1Tbps,并启用毫米波、太赫兹、可见光等尖端科技,有望打造出空天地融合的立体网络,预计6G数据传输速率有望比5G快100倍,时延达到亚毫秒级水平.香农公式是被广泛公认的通信理论基础和研究依据,它表示:在受噪声干扰的信道中,最大信息传递率取决于信道宽带 , 信道内信号的平均功率 , 信道内部的高斯噪声功率的大小,其中叫做信噪比.若不改变宽带 , 而将信噪比从11提升至499,则最大信息传递率会提升到原来的倍.(结果保留一位小数)22. 计算:.23. 生物入侵是指生物由原生存地侵入到另一个新的环境,从而对入侵地的生态系统造成危害的现象.若某入侵物种的个体平均繁殖数量为 , 一年四季均可繁殖,繁殖间隔T为相邻两代间繁殖所需的平均时间.在物种入侵初期,可用对数模型(为常数)来描述该物种累计繁殖数量与入侵时间K(单位:天)之间的对应关系,且 , 在物种入侵初期,基于现有数据得出 , .据此估计该物种累计繁殖数量比初始累计繁殖数量增加倍所需要的时间为( , )天.24. 实数 , 满足 , 则的最小值为.
三、解答题
-
25. 已知函数 和 有相同的最小值.(1)、求a;(2)、证明:存在直线 ,其与两条曲线 和 共有三个不同的交点,并且从左到右的三个交点的横坐标成等差数列.26. 已知各项均为正数的等差数列 , , , , 成等比数列.(1)、求的通项公式;(2)、设数列满足 , 为数列的前n项和, , 求证:.27. 已知数列 是首项为4,公差为2的等差数列.( 为常数, 且 ).
(Ⅰ)求证:数列 是等比数列;
(Ⅱ)当 时,设 ,求数列 的前 项和 .
28. 设数列 满足 ,且 , .(1)、证明:数列 为等比数列;(2)、设 ,求数列 的前 项和 .29. 已知函数 ,求证:(1)、函数 有且仅有一个零点;(2)、 .30. 已知函数 .(1)、求不等式 的解集;(2)、若不等式 对任意 恒成立,求 的取值范围.31. 已知函数 的图象在点 处的切线方程为 .(1)、当 时,证明: ;(2)、设函数 ,当 时,证明: ;(3)、若数列 满足: , , .证明: .32. 已知函数 ( ,且a为常数).(1)、若函数 的图象在 处的切线的斜率为 ( 为自然对数的底数),求a的值;(2)、若函数 在区间 上单调递增,求a的取值范围;(3)、已知 ,且 .求证: .33. 某公司欲投资一新型产品的批量生产,预计该产品的每日生产总成本价格)y(单位:万元)是每日产量x(单位:吨)的函数: .(1)、求当日产量为3吨时的边际成本(即生产过程中一段时间的总成本对该段时间产量的导数);(2)、记每日生产平均成本 求证: ;(3)、若财团每日注入资金可按数列 (单位:亿元)递减,连续注入 天,求证:这 天的总投入资金大于 亿元.