【备考2024】高考数学(函数版块)细点逐一突破训练:指数函数3
试卷更新日期:2023-08-17 类型:二轮复习
一、选择题
-
1. 设 , , ,则( )A、a<b<c B、b<c<a C、b<a<c D、c<a<b2. 设 ,则a , b , c的大小关系为( )A、 B、 C、 D、3. 设 ,则 的大小关系为( )A、 B、 C、 D、4. 设 , 其中是自然对数的底数 , 则( )A、 B、 C、 D、5. 设 , , 则( )A、 B、 C、 D、6. 函数的大致图象为( )A、
 B、
B、 C、
C、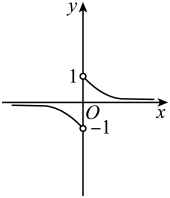 D、
D、 7. 已知 , , , 则( )A、 B、 C、 D、8. 已知 , , 且 , 则( )A、 B、 C、 D、9. 已知 , , , 则( )A、 B、 C、 D、10. 已知 , 则( )A、 B、 C、 D、11. 若 , 则一定有( )A、 B、 C、 D、12. 设 , , , 则 , , 的大小关系为( )A、 B、 C、 D、13. 已知函数在上先增后减,函数在上先增后减.若 , , , 则( )A、 B、 C、 D、
7. 已知 , , , 则( )A、 B、 C、 D、8. 已知 , , 且 , 则( )A、 B、 C、 D、9. 已知 , , , 则( )A、 B、 C、 D、10. 已知 , 则( )A、 B、 C、 D、11. 若 , 则一定有( )A、 B、 C、 D、12. 设 , , , 则 , , 的大小关系为( )A、 B、 C、 D、13. 已知函数在上先增后减,函数在上先增后减.若 , , , 则( )A、 B、 C、 D、二、填空题
-
14. 如图是一个算法流程图,若输出y的值为-2,则输入x的值是.
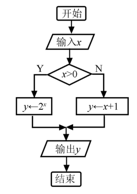 15. 已知函数 , .对于不相等的正实数 , ,设 , ,现有如下命题:
15. 已知函数 , .对于不相等的正实数 , ,设 , ,现有如下命题:①对于任意不相等的正实数 , ,都有 ;
②对于任意的a及任意不相等的正实数 , ,都有 ;
③对于任意的a,存在不相等的正实数 , ,使得 ;
④对于任意的a,存在不相等的正实数 , ,使得 .
其中真命题有(写出所有真命题的序号).
16. 设 , , ,则 , , 的大小关系是 . (按照从大到小的顺序排列)17. 设 ,则 按从小到大的顺序为 .18. 函数 在区间 上的最大值比最小值大 ,则 的值为.19. 设a,b,c均为正数,且ea=-lna,e-b=-lnb,e-c=lnc,则a,b,c按从小到大的顺序排列为。20. 已知函数 ( 且 )的图象恒过定点P,且点P在函数 的图象上,则 .21. 已知函数 ,若 ,则不等式 的解集为 , 若存在实数 ,使函数 有两个零点,则 的取值范围是 .22. 若函数 (a>0且a≠1)在定义域[m , n]上的值域是[m2 , n2](1<m<n),则a的取值范围是 .23. 设函数 的图象与 的图象关于直线 对称,且 ,则实数 .24. 函数 在 上的值域为 .三、解答题
-
25. 已知函数是指数函数.(1)、求实数的值;(2)、已知 , , 求的值域.26. 已知是上的奇函数.(1)、求实数的值;(2)、若关于的不等式在上有解,求实数的取值范围.27. 已知函数( , 且)满足.(1)、求的值;(2)、解不等式.28. 已知是幂函数,是指数函数,且满足 , .(1)、求函数 , 的解析式;(2)、若 , , 请判断“是的什么条件?(“充分不必要条件”或“必要不充分条件”或“充要条件”或“既不充分也不必要条件”).29. 已知 , 且 , 若函数在区间[a,2a]上的最大值与最小值之差为1.(1)、求a的值;(2)、解不等式;(3)、求函数的单调区间.30. 已知函数( , 且).(1)、若函数的图象过点 , 求b的值;(2)、若函数在区间上的最大值比最小值大 , 求a的值.31. 已知函数 , 且的图象经过点 .(1)、求的值;(2)、求在区间上的最大值;(3)、若 , 求证:在区间内存在零点.32. 已知奇函数 .(1)、求实数a的值;(2)、对任意的 , 不等式恒成立,求实数t的最大值.33. 为落实中央“精准扶贫”政策,让市民吃上放心蔬菜,某企业于2020年在其扶贫基地投入300万元研发资金用于蔬菜的开发与种植,并计划今后10年内在此基础上,每年投入的研发资金数比上一年增长 .(1)、以2021年为第1年,分别计算该企业第1年、第2年投入的研发资金数,并写出第 年该企业投入的研发资金数 (万元)与 的函数关系式以及函数的定义域;(2)、该企业从哪年开始,每年投入的研发资金数将超过600万元?