【备考2024】高考数学(函数版块)细点逐一突破训练:指数函数2
试卷更新日期:2023-08-17 类型:二轮复习
一、选择题
-
1. 若 , 则的大小关系为( )A、 B、 C、 D、2. 已知 , , , 则( )A、 B、 C、 D、3. 函数 在区间 的图像大致为( )A、

B、
B、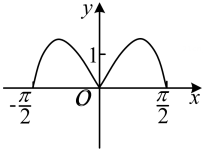
C、
C、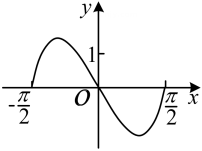
D、
D、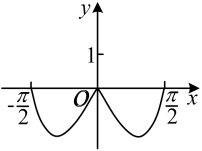
4. 函数 的图象大致是()A、
4. 函数 的图象大致是()A、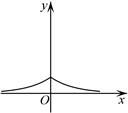 B、
B、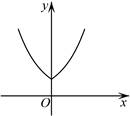 C、
C、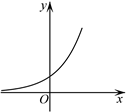 D、
D、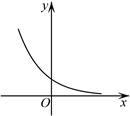 5. 已知集合 , , 则( ).A、 B、 C、 D、6. 若 , , , 则( )A、 B、 C、 D、7. 设集合 , 则的元素个数为( )A、3 B、4 C、9 D、无穷多个8. 若 , 则( )A、 B、 C、 D、9. 已知 , , , 则( )A、 B、 C、 D、10. 已知 , 则( )A、 B、 C、 D、11. 已知集合 , , 则( )A、 B、 C、 D、12. 已知 , 则( )A、 B、 C、 D、13. 已知函数 , 若成立,则实数a的取值范围为( )A、 B、 C、 D、14. 设 , 则的大小关系为( )A、 B、 C、 D、
5. 已知集合 , , 则( ).A、 B、 C、 D、6. 若 , , , 则( )A、 B、 C、 D、7. 设集合 , 则的元素个数为( )A、3 B、4 C、9 D、无穷多个8. 若 , 则( )A、 B、 C、 D、9. 已知 , , , 则( )A、 B、 C、 D、10. 已知 , 则( )A、 B、 C、 D、11. 已知集合 , , 则( )A、 B、 C、 D、12. 已知 , 则( )A、 B、 C、 D、13. 已知函数 , 若成立,则实数a的取值范围为( )A、 B、 C、 D、14. 设 , 则的大小关系为( )A、 B、 C、 D、二、填空题
-
15. 已知 , 则的值域是 ;16. 已知函数 , 则;若 , 不等式恒成立,则实数a的取值范围是 .17. 若函数在区间上的最大值与最小值的差为2,则 .18. 已知是定义在上的函数,其值域为 , 则可以是.(写出一个满足条件的函数表达式即可)19. 不等式的解集为 .20. 某公司通过统计分析发现,工人工作效率E与工作年限 , 劳累程度 , 劳动动机相关,并建立了数学模型 .
已知甲、乙为该公司的员工,给出下列四个结论:
①甲与乙劳动动机相同,且甲比乙工作年限长,劳累程度弱,则甲比乙工作效率高;
@甲与乙劳累程度相同,且甲比乙工作年限长,劳动动机高,则甲比乙工作效率高;
③甲与乙工作年限相同,且甲比乙工作效率高,劳动动机低,则甲比乙劳累程度强:
④甲与乙劳动动机相同,且甲比乙工作效率高,工作年限短.则甲比乙劳累程度弱.
其中所有正确结论的序号是 .
21. 写出一个同时具有下列性质①②③的函数:.①;②;③.
22. 写出一个同时具有下列性质①②③的函数: .①;②;③ .
23. 函数 ( 且 )的图象恒过定点A,若点A在直线 上,其中 , ,则mn的最大值为.24. 已知函数 在R上存在最小值,则m的取值范围是.25. 函数概念最早出现在格雷戈里的文章《论圆和双曲线的求积》(1667年)中.他定义函数是这样一个量:它是从一些其他量出发,经过一系列代数运算而得到的,或者经过任何其他可以想象到的运算得到的.若一个量 ,而 所对应的函数值 可以通过 得到,并且对另一个量 ,若 ,则都可以得到 .根据自己所学的知识写出一个能够反映 与 的函数关系式:.三、解答题
-
26. 已知均为不是1的正实数,设函数的表达式为 .(1)、设且 , 求x的取值范围;(2)、设 , , 记 , , 现将数列中剔除的项后、不改变其原来顺序所组成的数列记为 , 求的值.27. 已知函数 .(a为实常数)(1)、讨论函数 的奇偶性,并说明理由;(2)、当 为奇函数时,对任意 ,不等式 恒成立,求实数u的最大值.28. 已知数 ,其中 为自然对数底数(1)、讨论函数 的单调性;(2)、若a>0,函数 对任意的 都成立,求a+b的最大值.29. 已知函数f(x)=( )ax , a为常数,且函数的图象过点(﹣1,2).(1)、求a的值;(2)、若g(x)=4﹣x﹣2,且g(x)=f(x),求满足条件的x的值.30. 在数学中,双曲函数是与三角函数类似的函数,最基本的双曲函数是双曲正弦函数与双曲余弦函数,其中双曲正弦函数: , 双曲余弦函数:.(e是自然对数的底数,).(1)、计算的值;(2)、类比两角和的余弦公式,写出两角和的双曲余弦公式: , 并加以证明;(3)、若对任意 , 关于的方程有解,求实数的取值范围.31. 已知函数为偶函数.(1)、求出a的值,并写出单调区间;(2)、若存在使得不等式成立,求实数b的取值范围.32. 若函数是指数函数,求函数在区间上的值域.