【备考2024】高考数学（函数版块）细点逐一突破训练：幂函数

试卷更新日期：2023-08-17 类型：二轮复习

进入出卷网下载

一、选择题

1. 若 $a = 1.0 1^{0.5} ， b = 1.0 1^{0.6} ， c = 0 . 6^{0.5}$ ，则 $a ， b ， c$ 的大小关系为（）

A、 $c > a > b$ B、 $c > b > a$ C、 $a > b > c$ D、 $b > a > c$

查看试题解析
2. 已知a= $2^{\frac{4}{3}}$ ，b= $3^{\frac{2}{3}}$ ，c= $25^{\frac{1}{3}}$ ，则（　　）

A、b＜a＜c B、a＜b＜c C、b＜c＜a D、c＜a＜b

查看试题解析
3. 已知幂函数 $f (x)$ 的图象经过点 $A (3 ， 27)$ 与点 $B (t ， 64)$ ， $a = l o g_{0.1} t$ ， $b = 0 . 2^{t}$ ， $c = t^{0.1}$ ，则（）

A、 $c < a < b$ B、 $a < b < c$ C、 $b < a < c$ D、 $c < b < a$

查看试题解析
4. 已知幂函数 $f (x) = x^{α}$ 满足 $2 f (2) = f (16)$ ，若 $a = f (\log_{4} 2)$ ， $b = f (\ln 2)$ ， $c = f (5^{- \frac{1}{2}})$ ，则 $a$ ， $b$ ， $c$ 的大小关系是（）

A、 $a > c > b$ B、 $a > b > c$ C、 $b > a > c$ D、 $b > c > a$

查看试题解析
5. 设正实数 $a$ ， $b$ ， $c$ 分别满足 $a \cdot 2^{a} = 1$ ， $b \cdot l o g_{2} b = 1$ ， $c^{2} \cdot {(\frac{1}{2})}^{c} = 1$ 则a， $b$ ， c的大小关系为（）

A、 $b > c > a$ B、 $c > b > a$ C、 $c > a > b$ D、 $a > c > b$

查看试题解析
6. 不等式 ${(\frac{1}{2})}^{x} \leq \sqrt{x}$ 的解集是（）

A、 $[0 ， \frac{1}{2}]$ B、 $[\frac{1}{2} ， + \infty)$ C、 $[0 ， \frac{\sqrt{2}}{2}]$ D、 $[\frac{\sqrt{2}}{2} ， + \infty)$

查看试题解析
7. 已知 $a = x^{\frac{1}{3}} ， b = {(\frac{1}{3})}^{x} ， c = \log_{\frac{1}{3}} x$ ，则下列说法正确的是（）

A、当 $a = b$ 时， $c < a$ B、当 $b = c$ 时， $a < c$ C、当 $a = c$ 时， $b < a$ D、当 $c = 0$ 时， $a < b$

查看试题解析
8. 下列说法中正确的是（）

A、“ $x > 5$ ”是“ $x > 3$ ”的必要不充分条件 B、命题“对 $\forall x \in R$ ，恒有 $x^{2} + 1 > 0$ ”的否定是“ $\exists x \in R$ ，使得 $x^{2} + 1 < 0$ ” C、在同一直角坐标系中，函数 $y = 2^{x}$ 与 $y = l g x$ 的图象关于直线 $y = x$ 对称 D、若幂函数 $f (x) = m x^{α}$ 过点 $(\frac{1}{2} ， \frac{\sqrt{2}}{2})$ ，则 $m + α = \frac{3}{2}$

查看试题解析
9. 已知幂函数 $f (x)$ 的图象经过点 $(4 ， 2)$ ，则下列命题正确的有（）．

A、函数 $f (x)$ 的定义域为 $R$ B、函数 $f (x)$ 为非奇非偶函数 C、过点 $P (0 ， \frac{1}{2})$ 且与 $f (x)$ 图象相切的直线方程为 $y = \frac{1}{2} x + \frac{1}{2}$ D、若 $x_{2} > x_{1} > 0$ ，则 $\frac{f (x_{1}) + f (x_{2})}{2} > f (\frac{x_{1} + x_{2}}{2})$

查看试题解析
10. 已知函数 $f (x) = \frac{l n x}{x}$ ，若 $x_{1} \neq x_{2}$ 时，有 $f (x_{1}) = f (x_{2}) = m$ ， $π$ 是圆周率， $e = 2.71828 ⋯$ 为自然对数的底数，则下列结论正确的是（）

A、 $f (x)$ 的图象与 $x$ 轴有两个交点 B、 $m < \frac{1}{e}$ C、若 $0 < x_{1} < x_{2} < 4$ ，则 $2 < x_{1} < e$ D、若 $a = e^{3}$ ， $b = 3^{e}$ ， $c = e^{π}$ ， $d = π^{e}$ ， $s = 3^{π}$ ， $t = π^{3}$ ，则 $s$ 最大

查看试题解析
11. 下面叙述正确的有（）

A、不等式 $(2 x - 1)^{- \frac{2}{3}} > (x + 1)^{- \frac{2}{3}}$ 的解集为 $(0 ， 2)$ ； B、若函数 $f (x) = l g (x^{2} + a x + 1)$ 的值域为 $R$ ，则 $Δ = a^{2} - 4 \geq 0$ ； C、若函数 $f (x) = l g (x^{2} + a x + 1)$ 的定义域为 $R$ ，则 $Δ = a^{2} - 4 < 0$ ； D、函数 $f (x) = 4^{x} - 2^{x + 2} - 1$ 在 $[0 ， 2]$ 上单调递减．

查看试题解析
12. 幂函数y=x^α ，当α取不同的正数时，在区间[0，1]上它们的图象是一族美丽的曲线（如图）．设点A（1，0），B（0，1），连接AB，线段AB恰好被其中的两个幂函数y=x^α ， y=x^β的图象三等分，即有BM=MN=NA．那么，αβ=（）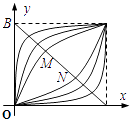

A、1 B、2 C、 $\frac{1}{2}$ D、 $\frac{1}{3}$

查看试题解析
13. 幂函数y=x^α ，当α取不同的正数时，在区间[0，1]上它们的图象是一族美丽的曲线（如图）．设点A（1，0），B（0，1），连接AB，线段AB恰好被其中的两个幂函数y=x^α ， y=x^β的图象三等分，即有BM=MN=NA．那么，αβ=（）

A、1 B、2 C、 $\frac{1}{2}$ D、 $\frac{1}{3}$

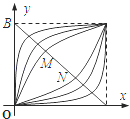查看试题解析

二、填空题

14. 写出一个同时具有下列性质①②③的函数 $f (x) ：$ ．
① $f (x_{1} x_{2}) = f (x_{1}) f (x_{2})$ ；②当 $x \in (0 ， + \infty)$ 时， $f^{'} (x) > 0$ ；③ $f^{'} (x)$ 是奇函数．

查看试题解析
15. 已知 $α \in ｛ - 2 ， - 1 ， - \frac{1}{2} ， \frac{1}{2} ， 1 ， 2 ， 3 ｝$ ，若幂函数 $f (x) = x^{a}$ 为奇函数，且在 $（ 0 ， + \infty ）$ 上递减，则α=

查看试题解析
16. 若函数 $y = x^{a}$ 的图像经过点 $(2 ， 16)$ 与 $(3 ， m)$ ，则m的值为．

查看试题解析
17. 已知幂函数 $y = f (x)$ 的图象过点 $(4, \frac{1}{2})$ ，则 $f (x) =$ .

查看试题解析
18. 已知幂函数 $y = f (x)$ 的图像过点 $(2, \sqrt{2}),$ 则 $f (4) =$ ．

查看试题解析
19. 已知函数 $f (x) = {\begin{matrix} 2 x^{2} - 2 ， x \geq 0 \\ - \frac{4}{3} x ， x < 0 \end{matrix}$ ，函数 $g (x) = f (x) + \sqrt{1 - x^{2}} + | f (x) - \sqrt{1 - x^{2}} | - 2 a x + 4 a$ 有三个零点，则实数 $a$ 的取值范围为．

查看试题解析
20. 已知函数 $y = f (x)$ 和 $y = g (x)$ 的表达式分别为 $f (x) = \sqrt{- x^{2} - 4 x}$ ， $g (x) = x | x^{2} - a |$ ，若对任意 $x_{1} \in [1 ， \sqrt{2}]$ ，若存在 $x_{2} \in [- 3 ， 0]$ ，使得 $g (x_{1}) < f (x_{2})$ ，则实数 $a$ 的取值范围是.

查看试题解析
21. 某公司通过统计分析发现，工人工作效率E与工作年限 $r (r > 0)$ ，劳累程度 $T (0 < T < 1)$ ，劳动动机 $b (1 < b < 5)$ 相关，并建立了数学模型 $E = 10 - 10 T \cdot b^{- 0.14 r}$ ．
已知甲、乙为该公司的员工，给出下列四个结论：
①甲与乙劳动动机相同，且甲比乙工作年限长，劳累程度弱，则甲比乙工作效率高；
@甲与乙劳累程度相同，且甲比乙工作年限长，劳动动机高，则甲比乙工作效率高；
③甲与乙工作年限相同，且甲比乙工作效率高，劳动动机低，则甲比乙劳累程度强：
④甲与乙劳动动机相同，且甲比乙工作效率高，工作年限短．则甲比乙劳累程度弱．
其中所有正确结论的序号是．

查看试题解析
22. 幂函数 $f (x) = x^{- 2}$ 的单调增区间为.

查看试题解析
23. 已知函数 $f (x) = (m^{2} - 2 m - 2) x^{m^{2} + m + 3}$ 是幂函数，且在 $(0 ， + ∞)$ 上单调递增，则实数 $m =$ .

查看试题解析
24. 已知函数 $f (x) = x^{n}$ 的图像经过点 $(2 ， 8)$ ，若 $f (2 x) + f (1 - x) < 0$ ，则 $x$ 的取值范围为.

查看试题解析

三、解答题

25. 已知 $f (x) = (m^{2} - 2 m - 7) x^{m - 2}$ 是幂函数，且在 $(0 ， + ∞)$ 上单调递增．

(1)、求 $m$ 的值；

(2)、求函数 $g (x) = f (x) - (2 a - 1) x + 1$ 在区间 $[2 ， 4]$ 上的最小值 $h (a)$ ．

查看试题解析
26. 已知函数 $f (x) = \frac{1}{3} (a - 2) x^{2} + (b - 8) x + c - 1 (x \in R)$ .

(1)、如果函数 $f (x)$ 为幂函数，试求实数a、b、c的值；

(2)、如果 $a > 0$ 、 $b > 0$ ，且函数 $f (x)$ 在区间 $[\frac{1}{2} ， 3]$ 上单调递减，试求ab的最大值.

查看试题解析
27. 已知幂函数 $f (x) = (m^{2} - 3 m - 9) x^{m - 3}$ 在 $(0 ， + ∞)$ 上单调递减.

(1)、求 $m$ 的值；

(2)、若 $(2 a - 1)^{m} > (a + 2)^{m}$ ，求 $a$ 的取值范围.

查看试题解析
28. 已知函数 $f (x) = a \cdot 2^{x} + b$ ，幂函数 $g (x) = (m^{2} - 3) x^{\frac{m}{3}}$ ，且函数 $f (x)$ 的图像过点 $(0 ， 0)$ ，当 $x$ 趋向于负无穷大时， $f (x)$ 的图像无限接近于直线 $y = - 1$ 但又不与该直线相交：函数 $g (x)$ 在区间 $(0 ， + \infty)$ 上单调递增.

(1)、分别求出 $f (x)$ ， $g (x)$ 的解析式，并在同一直角坐标系中作出两函数的草图；

(2)、定义 $\forall x \in R$ ， $m (x)$ 表示 $f (x)$ ， $g (x)$ 中的最小者，记为 $m (x) = m i n {f (x) ， g (x)}$ ，例如，当 $x = 2$ 时 $m (2)$ 表示 $f (2)$ ， $g (2)$ 中的最小者.请结合（1）中的两个函数图象分别用图象法（草图）与解析法表示 $m (x)$ .

查看试题解析
29.

(1)、计算 $(\lg \frac{1}{4} - \lg 25) \div 100^{\frac{1}{2}}$ 的值；

(2)、已知 $\tan α = 2$ ，求 $\frac{2 \sin α - 3 \cos α}{4 \sin α - 9 \cos α}$ 和 $\sin α \cos α$ 的值．

查看试题解析
30. 已知幂函数 $f (x) = {(m - 1)}^{2} x^{m^{2} - 4 m + 2}$ 在 $(0 ， + \infty)$ 上单调递增，函数 $g (x) = 2^{x} - k$ ；

(1)、求m的值；

(2)、当 $x \in [1 ， 2]$ 时，记 $f (x)$ 、 $g (x)$ 的值域分别是A、B，若 $A \cup B = A$ ，求实数k的取值范围；

查看试题解析
31. 已知幂函数 $f (x) = (m^{2} - 3 m + 3) x^{m}$ 的图象关于 $y$ 轴对称，集合 $A = {x | 1 - a < x \leq 3 a + 1}$ .

(1)、求 $m$ 的值；

(2)、当 $x \in [\frac{\sqrt{2}}{2} ， 2]$ 时， $f (x)$ 的值域为集合 $B$ ，若 $x \in B$ 是 $x \in A$ 成立的充分不必要条件，求实数 $a$ 的取值范围.

查看试题解析
32. 已知幂函数 $f (x) = x^{α}$ 的图象经过点 $(\sqrt{2} ， 2)$ ．

(1)、求函数 $f (x)$ 的解析式；

(2)、若函数 $f (x)$ 满足条件 $f (2 - a) > f (a - 1)$ ，试求实数 $a$ 的取值范围．

查看试题解析
33. 某生产制造企业统计了近10年的年利润 $y$ （千万元）与每年投入的某种材料费用 $x$ （十万元）的相关数据，作出如下散点图：

选取函数 $y = a \cdot x^{b} (b > 0 ， a > 0)$ 作为每年该材料费用 $x$ 和年利润 $y$ 的回归模型.若令 $m = l n x ， n = l n y ， m_{i} = l n x_{i} ， n_{i} = l n y_{i}$ ，则 $n = b m + l n a$ ，得到相关数据如表所示：

$\sum_{i = 1}^{10} m_{i} n_{i}$

$\sum_{i = 1}^{10} m_{i}$

$\sum_{i = 1}^{10} n_{i}$

$\sum_{i = 1}^{10} m_{i}^{2}$

31.5

15

15

49.5

参考数据： $\frac{10}{e} \approx 3.679 ， 3.67 9^{2} \approx 13.535 ， 3.67 9^{3} \approx 49.795$ .

(1)、求出 $y$ 与 $x$ 的回归方程；

(2)、计划明年年利润额突破1亿，则该种材料应至少投入多少费用？（结果保留到万元）.

查看试题解析
34. 济南市地铁项目正在加火如荼的进行中，通车后将给市民出行带来便利，已知某条线路通车后，列车的发车时间间隔t（单位：分钟）满足 $2 \leq t \leq 20$ ，经市场调研测算，列车载客量与发车时间间隔t相关，当 $10 \leq t \leq 20$ 时列车为满载状态，载客量为500人，当 $2 \leq t < 10$ 时，载客量会减少，减少的人数与 $(10 - t)$ 的平方成正比，且发车时间间隔为2分钟时的载客量为372人，记列车载客量为 $p (t)$ .

(1)、求 $p (t)$ 的表达式，并求当发车时间间隔为5分钟时，列车的载客量；

(2)、若该线路每分钟的净收益为 $Q (t) = \frac{8 p (t) - 2656}{t} - 60$ （元），问当发车时间间隔为多少时，该线路每分钟的净收益最大，并求出最大值.

查看试题解析
35. 已知 $x + x^{- 1} = 5$

(1)、求 $\frac{x^{\frac{1}{2}} + x^{- \frac{1}{2}}}{x^{2} + x^{- 2} + 3}$ 的值

(2)、求 $x^{2} - x^{- 2}$

查看试题解析
36. 已知幂函数（m∈Z）的图象关于y轴对称，且在区间（0，+∞）为减函数

(1)、求m的值和函数f（x）的解析式

(2)、解关于x的不等式f（x+2）＜f（1﹣2x）．

查看试题解析

$\sum_{i = 1}^{10} m_{i} n_{i}$	$\sum_{i = 1}^{10} m_{i}$	$\sum_{i = 1}^{10} n_{i}$	$\sum_{i = 1}^{10} m_{i}^{2}$
31.5	15	15	49.5