【备考2024】高考数学(函数版块)细点逐一突破训练:函数的图象与图象变化
试卷更新日期:2023-08-17 类型:二轮复习
一、选择题
-
1. 将函数 的图像向左平移 个单位长度后得到曲线C,若C关于y轴对称,则 的最小值是( )A、 B、 C、 D、2. 已知函数 ,则图象为如图的函数可能是( )
 A、 B、 C、 D、3. 函数 的图像大致为( )A、
A、 B、 C、 D、3. 函数 的图像大致为( )A、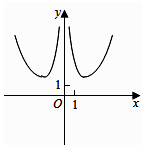 B、
B、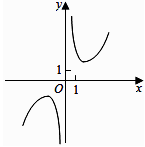 C、
C、 D、
D、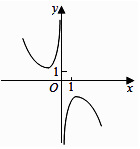 4. 设D是含数1的有限实数集, 是定义在D上的函数,若 的图像绕原点逆时针旋转 后与原图像重合,则在以下各项中, 的可能取值只能是( )A、 B、 C、 D、05. 已知函数 , , 若函数在上的大致图象如图所示,则的解析式可能是( )
4. 设D是含数1的有限实数集, 是定义在D上的函数,若 的图像绕原点逆时针旋转 后与原图像重合,则在以下各项中, 的可能取值只能是( )A、 B、 C、 D、05. 已知函数 , , 若函数在上的大致图象如图所示,则的解析式可能是( )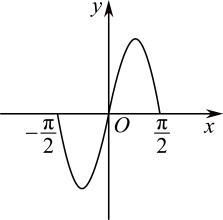 A、 B、 C、 D、6. 某地区今年夏天迎来近50年来罕见的高温极端天气,当地气象部门统计了八月份每天的最高气温和最低气温,得到如下图表:
A、 B、 C、 D、6. 某地区今年夏天迎来近50年来罕见的高温极端天气,当地气象部门统计了八月份每天的最高气温和最低气温,得到如下图表:某地区2022年8月份每天最高气温与最低气温
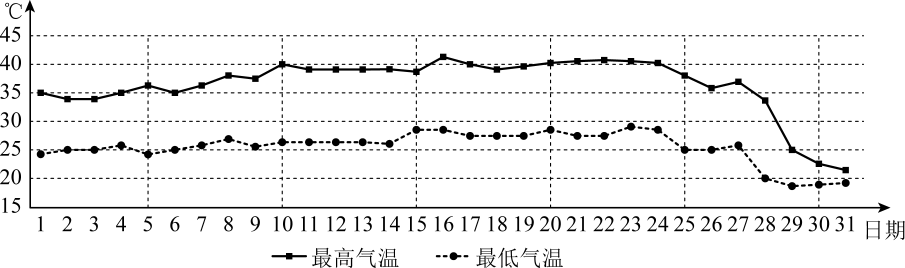
根据图表判断,以下结论正确的是()
A、8月每天最高气温的平均数低于35℃ B、8月每天最高气温的中位数高于40℃ C、8月前半月每天最高气温的方差大于后半月最高气温的方差 D、8月每天最高气温的方差大于每天最低气温的方差7. 四参数方程的拟合函数表达式为 , 常用于竞争系统和免疫检测,它的图象是一个递增(或递减)的类似指数或对数曲线,或双曲线(如),还可以是一条S形曲线,当 , , , 时,该拟合函数图象是( )A、类似递增的双曲线 B、类似递增的对数曲线 C、类似递减的指数曲线 D、是一条S形曲线8. 函数的图象可能是( )A、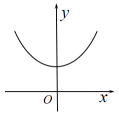 B、
B、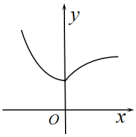 C、
C、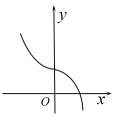 D、
D、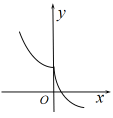 9. 函数的图像大致为( )A、
9. 函数的图像大致为( )A、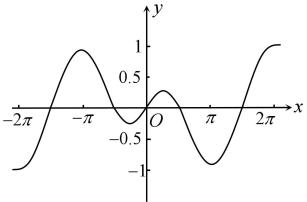 B、
B、 C、
C、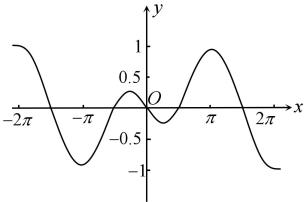 D、
D、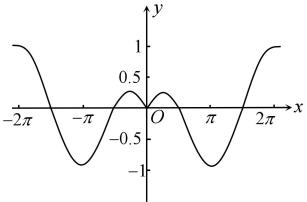 10. 已知函数 , , 且 , 则的最小值是( )A、-2 B、 C、-1 D、11. 已知函数 , , 则图象如图的函数可能是( )
10. 已知函数 , , 且 , 则的最小值是( )A、-2 B、 C、-1 D、11. 已知函数 , , 则图象如图的函数可能是( )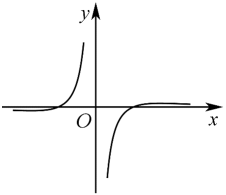 A、 B、 C、 D、12. 已知函数 ,若方程 的4个不同实根从小到大依次为 ,有以下三个结论:① 且 ;②当 时, 且 ;③ .其中正确的结论个数为( )A、0 B、1 C、2 D、313. 函数 的图象大致为( )A、
A、 B、 C、 D、12. 已知函数 ,若方程 的4个不同实根从小到大依次为 ,有以下三个结论:① 且 ;②当 时, 且 ;③ .其中正确的结论个数为( )A、0 B、1 C、2 D、313. 函数 的图象大致为( )A、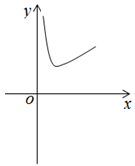 B、
B、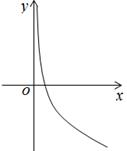 C、
C、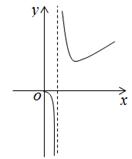 D、
D、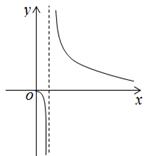 14. 已知函数 (e为自然对数的底数),若关于x的不等式 解集中恰含有一个整数,则实数a的取值范围为( )A、 B、 C、 D、
14. 已知函数 (e为自然对数的底数),若关于x的不等式 解集中恰含有一个整数,则实数a的取值范围为( )A、 B、 C、 D、二、填空题
-
15. 已知函数 ( , )的部分图像如图所示,则 .
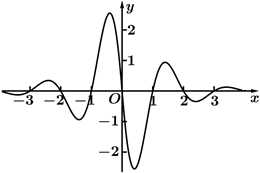 16. 写出一个同时满足下列两个条件的非常数函数
16. 写出一个同时满足下列两个条件的非常数函数①当 时, ;② 为偶函数
17. 设定义域为R的函数 若关于x的方程 有7个不同的实数根,则实数 .18. 已知函数 的图象关于点 对称,则 .
19. 已知函数 ,若对任意实数 ,关于 的不等式 在区间 上总有解,则实数 的取值范围为.20. 已知关于 的方程 在 上有3个相异实根,则实数 的取值范围是 .21. 已知函数 ,若关于x的方程f(x)=k有两个不同的实数根,则实数k的取值范围是 .
22. 如图,正方形 的边长为2, 为 的中点,射线 从 出发,绕着点 顺时针方向旋转至 ,在旋转的过程中,记 为 , 所经过的在正方形 内的区域(阴影部分)的面积 ,那么对于函数 有以下三个结论:
① ;② 对任意 ,都有 ;
③ 对任意 ,且 ,都有 ;
其中所有正确结论的序号是;
23. 已知 满足 当 时, 若函数 在 内有2个零点,则实数 的取值范围是.
24. 已知函数g(x)=(a+1)x﹣2+1(a>0)的图象恒过定点A,且点A又在函数 (x+a)的图象上.则实数a= .三、解答题
-
25. 已知函数f(x)=|x-2|, g(x) =|2x + 3|-|2x-1|.
 (1)、画出f(x)和y=g(x)的图像;(2)、若f(x+a)≥g(x),求a的取值范围.26. 如图,在海岸线 一侧有一休闲游乐场,游乐场的前一部分边界为曲线段 ,该曲线段是函数 , 的图像,图像的最高点为 .边界的中间部分为长1千米的直线段 ,且 .游乐场的后一部分边界是以 为圆心的一段圆弧 .
(1)、画出f(x)和y=g(x)的图像;(2)、若f(x+a)≥g(x),求a的取值范围.26. 如图,在海岸线 一侧有一休闲游乐场,游乐场的前一部分边界为曲线段 ,该曲线段是函数 , 的图像,图像的最高点为 .边界的中间部分为长1千米的直线段 ,且 .游乐场的后一部分边界是以 为圆心的一段圆弧 .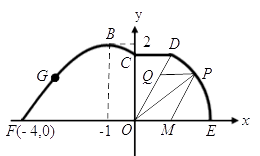 (1)、求曲线段 的函数表达式;
(1)、求曲线段 的函数表达式;
(2)、曲线段 上的入口 距海岸线 最近距离为1千米,现准备从入口 修一条笔直的景观路到 ,求景观路 长;(3)、如图,在扇形 区域内建一个平行四边形休闲区 ,平行四边形的一边在海岸线 上,一边在半径 上,另外一个顶点P在圆弧 上,且 ,求平行四边形休闲区 面积的最大值及此时 的值.27. 设函数 ( 且 ),当点 是函数 图象上的点时,点 是函数 图象上的点.(1)、写出函数 的解析式;(2)、把 的图象向左平移a个单位得到 的图象,函数 ,是否存在实数 ,使函数 的定义域为 ,值域为 .如果存在,求出 的值;如果不存在,说明理由;(3)、若当 时,恒有 ,试确定a的取值范围.28. 已知直线l: (t为参数),曲线C1: (θ为参数).(Ⅰ)设l与C1相交于A,B两点,求|AB|;
(Ⅱ)若把曲线C1上各点的横坐标压缩为原来的 倍,纵坐标压缩为原来的 倍,得到曲线C2 , 设点P是曲线C2上的一个动点,求它到直线l的距离的最小值.
29. 已知直线l: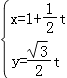 (t为参数),曲线C1:
(t为参数),曲线C1: 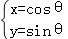 (θ为参数).
(θ为参数).(Ⅰ)设l与C1相交于A,B两点,求|AB|;
(Ⅱ)若把曲线C1上各点的横坐标压缩为原来的 倍,纵坐标压缩为原来的 倍,得到曲线C2 , 设点P是曲线C2上的一个动点,求它到直线l的距离的最小值.
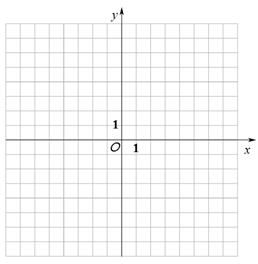
30. 已知函数 且点(4,2)在函数f(x)的图象上.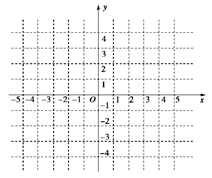 (1)、求函数f(x)的解析式,并在图中的直角坐标系中画出函数f(x)的图象;(2)、求不等式f(x)<1的解集;(3)、若方程f(x)-2m=0有两个不相等的实数根,求实数m的取值范围.31. 已知函数 是定义在 上的偶函数,且当 时, .
(1)、求函数f(x)的解析式,并在图中的直角坐标系中画出函数f(x)的图象;(2)、求不等式f(x)<1的解集;(3)、若方程f(x)-2m=0有两个不相等的实数根,求实数m的取值范围.31. 已知函数 是定义在 上的偶函数,且当 时, .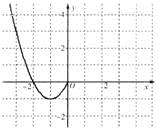 (1)、已画出函数 在 轴左侧的图像,如图所示,请补出完整函数 的图像,并根据图像写出函数 的增区间;(2)、写出函数 的解析式和值域.32. 已知定义在区间 上的函数 的图象关于直线 对称,当 时,函数 ,其图象如图所示.
(1)、已画出函数 在 轴左侧的图像,如图所示,请补出完整函数 的图像,并根据图像写出函数 的增区间;(2)、写出函数 的解析式和值域.32. 已知定义在区间 上的函数 的图象关于直线 对称,当 时,函数 ,其图象如图所示.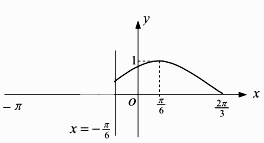 (1)、求函数 在 的表达式;(2)、求方程 解的集合;(3)、求不等式 的解集.33. 平面直角坐标系中,将曲线 (α为参数)上的每一点纵坐标不变,横坐标变为原来的一半,然后整个图象向右平移1个单位,最后横坐标不变,纵坐标变为原来的2倍得到曲线C1 . 以坐标原点为极点,x的非负半轴为极轴,建立的极坐标中的曲线C2的方程为ρ=4sinθ,求C1和C2公共弦的长度.34. 已知二次函数f(x)=x2﹣ax+3,且对任意的实数x都有f(4﹣x)=f(x)成立.(1)、求实数a的值;(2)、求函数f(x)在区间[0,3]上的值域;(3)、要得到函数y=x2的图象只需要将二次函数y=f(x)的图象做怎样的变换得到.35. 已知函数f(x)=ax﹣a+1,(a>0且a≠1)恒过定点(2,2).(1)、求实数a;(2)、在(1)的条件下,将函数f(x)的图象向下平移1个单位,再向左平移a个单位后得到函数g(x),设函数g(x)的反函数为h(x),求h(x)的解析式;(3)、对于定义在(1,4]上的函数y=h(x),若在其定义域内,不等式[h(x)+2]2≤h(x2)+h(x)m+6恒成立,求m的取值范围.36. 已知函数f(x)=log2(x+1).(1)、将函数f(x)的图象上的所有点向右平行移动1个单位得到函数g(x)的图象,写出函数g(x)的表达式;(2)、若关于x的函数y=g2(x)﹣mg(x2)+3在[1,4]上的最小值为2,求m的值.
(1)、求函数 在 的表达式;(2)、求方程 解的集合;(3)、求不等式 的解集.33. 平面直角坐标系中,将曲线 (α为参数)上的每一点纵坐标不变,横坐标变为原来的一半,然后整个图象向右平移1个单位,最后横坐标不变,纵坐标变为原来的2倍得到曲线C1 . 以坐标原点为极点,x的非负半轴为极轴,建立的极坐标中的曲线C2的方程为ρ=4sinθ,求C1和C2公共弦的长度.34. 已知二次函数f(x)=x2﹣ax+3,且对任意的实数x都有f(4﹣x)=f(x)成立.(1)、求实数a的值;(2)、求函数f(x)在区间[0,3]上的值域;(3)、要得到函数y=x2的图象只需要将二次函数y=f(x)的图象做怎样的变换得到.35. 已知函数f(x)=ax﹣a+1,(a>0且a≠1)恒过定点(2,2).(1)、求实数a;(2)、在(1)的条件下,将函数f(x)的图象向下平移1个单位,再向左平移a个单位后得到函数g(x),设函数g(x)的反函数为h(x),求h(x)的解析式;(3)、对于定义在(1,4]上的函数y=h(x),若在其定义域内,不等式[h(x)+2]2≤h(x2)+h(x)m+6恒成立,求m的取值范围.36. 已知函数f(x)=log2(x+1).(1)、将函数f(x)的图象上的所有点向右平行移动1个单位得到函数g(x)的图象,写出函数g(x)的表达式;(2)、若关于x的函数y=g2(x)﹣mg(x2)+3在[1,4]上的最小值为2,求m的值.