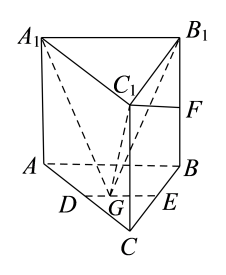【备考2024】高考数学(函数版块)细点逐一突破训练:二次函数在闭区间上的最值
试卷更新日期:2023-08-17 类型:二轮复习
一、选择题
-
1. 函数 ,试判断函数的奇偶性及最大值( )A、奇函数,最大值为2 B、偶函数,最大值为2 C、奇函数,最大值为 D、偶函数,最大值为2. 已知点 , 与直线 , 若在直线上存在点 , 使得 , 则实数的取值范围是( )A、 B、 C、 D、3. 如图,在等腰直角中,斜边 , 为线段BC上的动点,且 , 则的最小值为()
 A、 B、 C、4 D、64. 已知 , , 且 , 则( )A、的最小值是1 B、的最小值是 C、的最小值是4 D、的最小值是55. 已知二次函数()的值域为 , 则的最小值为( )A、-4 B、4 C、8 D、-86. 在菱形中, , 点在菱形所在平面内,则的最小值为( )A、 B、-3 C、 D、7. 已知点、在单位圆上, , 若 , 则的取值范围是( )A、 B、 C、 D、8. 已知的内角 , , 所对的边分别为 , , , , , . , 分别为线段 , 上的动点, , 则的最小值为( )A、 B、 C、 D、9. 在中, , , 有下述四个结论:
A、 B、 C、4 D、64. 已知 , , 且 , 则( )A、的最小值是1 B、的最小值是 C、的最小值是4 D、的最小值是55. 已知二次函数()的值域为 , 则的最小值为( )A、-4 B、4 C、8 D、-86. 在菱形中, , 点在菱形所在平面内,则的最小值为( )A、 B、-3 C、 D、7. 已知点、在单位圆上, , 若 , 则的取值范围是( )A、 B、 C、 D、8. 已知的内角 , , 所对的边分别为 , , , , , . , 分别为线段 , 上的动点, , 则的最小值为( )A、 B、 C、 D、9. 在中, , , 有下述四个结论:①若为的重心,则②若为边上的一个动点,则为定值2③若 , 为边上的两个动点,且 , 则的最小值为④已知为内一点,若 , 且 , 则的最大值为2
其中所有正确结论的编号是( )
A、①③ B、①④ C、②③ D、②④10. 已知的最小值为2,则的取值范围为( )A、 B、 C、 D、11. 已知点为圆上一点,点 , 当m变化时,线段长度的最小值为( )A、1 B、2 C、 D、二、填空题
-
12. 如图,E,F分别是三棱锥V-ABC两条棱AB,VC上的动点,且满足 则 的最小值为.
 13. 在边长为1的等边三角形ABC中,D为线段BC上的动点, 且交AB于点E . 且交AC于点F , 则 的值为; 的最小值为 .14. 如图,在四边形 中, , ,且 ,则实数 的值为 , 若 是线段 上的动点,且 ,则 的最小值为 .
13. 在边长为1的等边三角形ABC中,D为线段BC上的动点, 且交AB于点E . 且交AC于点F , 则 的值为; 的最小值为 .14. 如图,在四边形 中, , ,且 ,则实数 的值为 , 若 是线段 上的动点,且 ,则 的最小值为 . 15. 已知点是平面直角坐标系中关于轴对称的两点,且 . 若存在 , 使得与垂直,且 , 则的最小值为 .16. 已知边长为2的菱形中, , P、Q是菱形内切圆上的两个动点,且 , 则的最大值是 .17. 在长方形中, , , 为边的中点,分别为边上的动点,且 , 则的取值范围是 .18. 在棱长为1的正方体中,点分别是棱的中点,是侧面上的动点.且平面 , 则点的轨迹长为.点到直线的距离的最小值为.19. 已知 , 点D满足 , 点E为线段CD上异于C,D的动点,若 , 则的取值范围是.20. 在中, , , , 是所在平面内任意一点,则的最小值是.21. 已知菱形的边长为 , , ().当时,;当取得最小值时, .22. 已知正四棱锥的所有棱长都为1,点在侧棱上,过点且垂直于的平面截该棱锥,得到截面多边形 , 则的边数至多为 , 的面积的最大值为.
15. 已知点是平面直角坐标系中关于轴对称的两点,且 . 若存在 , 使得与垂直,且 , 则的最小值为 .16. 已知边长为2的菱形中, , P、Q是菱形内切圆上的两个动点,且 , 则的最大值是 .17. 在长方形中, , , 为边的中点,分别为边上的动点,且 , 则的取值范围是 .18. 在棱长为1的正方体中,点分别是棱的中点,是侧面上的动点.且平面 , 则点的轨迹长为.点到直线的距离的最小值为.19. 已知 , 点D满足 , 点E为线段CD上异于C,D的动点,若 , 则的取值范围是.20. 在中, , , , 是所在平面内任意一点,则的最小值是.21. 已知菱形的边长为 , , ().当时,;当取得最小值时, .22. 已知正四棱锥的所有棱长都为1,点在侧棱上,过点且垂直于的平面截该棱锥,得到截面多边形 , 则的边数至多为 , 的面积的最大值为.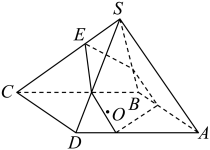 23. 在 中,角 所对边分别为 ,则 = , 的面积的最大值为 .24. 在矩形ABCD中, , , 点P在AB边上,则向量在向量上的投影向量的长度是 , 的最大值是 .
23. 在 中,角 所对边分别为 ,则 = , 的面积的最大值为 .24. 在矩形ABCD中, , , 点P在AB边上,则向量在向量上的投影向量的长度是 , 的最大值是 .三、解答题
-
25. 记 是公差不为0的等差数列 的前n项和,若 .(1)、求数列 的通项公式 ;(2)、求使 成立的n的最小值.26. 平面多边形中,三角形具有稳定性,而四边形不具有这一性质.如图所示,四边形的顶点在同一平面上,已知 .
 (1)、当长度变化时,是否为一个定值?若是,求出这个定值;若否,说明理由.(2)、记与的面积分别为和 , 请求出的最大值.27. 一企业生产某种产品,通过加大技术创新投入降低了每件产品成本,为了调查年技术创新投入(单位:千万元)对每件产品成本(单位:元)的影响,对近年的年技术创新投入和每件产品成本的数据进行分析,得到如下散点图,并计算得: , , , , .
(1)、当长度变化时,是否为一个定值?若是,求出这个定值;若否,说明理由.(2)、记与的面积分别为和 , 请求出的最大值.27. 一企业生产某种产品,通过加大技术创新投入降低了每件产品成本,为了调查年技术创新投入(单位:千万元)对每件产品成本(单位:元)的影响,对近年的年技术创新投入和每件产品成本的数据进行分析,得到如下散点图,并计算得: , , , , .
参考公式:对于一组数据、、、 , 其回归直线的斜率和截距的最小乘估计分别为: , .
(1)、根据散点图可知,可用函数模型拟合与的关系,试建立关于的回归方程;(2)、已知该产品的年销售额(单位:千万元)与每件产品成本的关系为.该企业的年投入成本除了年技术创新投入,还要投入其他成本千万元,根据(1)的结果回答:当年技术创新投入为何值时,年利润的预报值最大?(注:年利润=年销售额一年投入成本)
28. 已知数列是首项为9,公比为的等比数列.(1)、求的值;(2)、设数列的前项和为 , 求的最大值,并指出取最大值时的取值.29. 已知 .(1)、求的解集;(2)、已知在上恒成立,求实数a的取值范围.30. 已知 , , 且 , 证明:(1)、 ;(2)、 .31. 在直角坐标系中,曲线的方程为 . 为曲线上一动点,且 , 点的轨迹为曲线 . 以坐标原点为极点,轴正半轴为极轴建立极坐标系.(1)、求曲线 , 的极坐标方程;(2)、曲线的极坐标方程为 , 点为曲线上一动点,求的最大值.32. 已知函数.(1)、当时,求不等式的解集;(2)、若对任意 , 使得不等式恒成立,求实数a的取值范围.