【备考2024】高考数学(函数版块)细点逐一突破训练:二次函数的性质
试卷更新日期:2023-08-17 类型:二轮复习
一、选择题
-
1. 已知函数 在区间(-∞,1]是减函数,则实数a的取值范围是()A、[1,+∞) B、(-∞,1] C、[-1,+∞) D、(-∞,-1]2. 设a≠0,若x=a为函数 的极大值点,则( )A、a<b B、a>b C、ab<a2 D、ab>a23. 已知函数在区间上单调递增,则实数a的取值范围是( )A、 B、 C、 D、4. 已知双曲线 , , 为的左、右焦点, , 直线与的一支交于点 , 且 , 则的离心率最大值为( )A、 B、2 C、 D、5. 已知函数 , 则( )A、是一个最小正周期为的周期函数 B、是一个偶函数 C、在区间上单调递增 D、的最小值为 , 最大值为6. 如图圆柱内有一个内切球,这个球的直径恰好与圆柱的高相等, , 为圆柱上下底面的圆心,O为球心,EF为底面圆的一条直径,若球的半径 , 则( )
 A、球与圆柱的体积之比为 B、四面体CDEF的体积的取值范围为 C、平面DEF截得球的截面面积最小值为 D、若P为球面和圆柱侧面的交线上一点,则的取值范围为7. 已知双曲线的焦点分别是、 , 点P在双曲线C上,则下列结论正确的是( )A、的最大值为4 B、的最大值为2 C、的最小值为 D、的最小值为8. 点M、N在圆上,且M、N两点关于直线对称,则圆C的半径( )A、最大值为 B、最小值为 C、最小值为 D、最大值为9. 某车间需要对一个圆柱形工件进行加工,该工件底面半径15cm,高10cm,加工方法为在底面中心处打一个半径为rcm且和原工件有相同轴的圆柱形通孔.若要求工件加工后的表面积最大,则r的值应设计为( )
A、球与圆柱的体积之比为 B、四面体CDEF的体积的取值范围为 C、平面DEF截得球的截面面积最小值为 D、若P为球面和圆柱侧面的交线上一点,则的取值范围为7. 已知双曲线的焦点分别是、 , 点P在双曲线C上,则下列结论正确的是( )A、的最大值为4 B、的最大值为2 C、的最小值为 D、的最小值为8. 点M、N在圆上,且M、N两点关于直线对称,则圆C的半径( )A、最大值为 B、最小值为 C、最小值为 D、最大值为9. 某车间需要对一个圆柱形工件进行加工,该工件底面半径15cm,高10cm,加工方法为在底面中心处打一个半径为rcm且和原工件有相同轴的圆柱形通孔.若要求工件加工后的表面积最大,则r的值应设计为( ) A、 B、 C、4 D、510. 已知 ,则 的最大值为( )A、3 B、 C、4 D、11. 已知函数 , 则关于的不等式的解集是( )A、 B、 C、 D、12. 设函数 ,则下列结论中正确的是( )A、 的最小正周期为 B、 在 单调递减 C、 的图象关于直线 对称 D、 的值城为
A、 B、 C、4 D、510. 已知 ,则 的最大值为( )A、3 B、 C、4 D、11. 已知函数 , 则关于的不等式的解集是( )A、 B、 C、 D、12. 设函数 ,则下列结论中正确的是( )A、 的最小正周期为 B、 在 单调递减 C、 的图象关于直线 对称 D、 的值城为二、填空题
-
13. 如图,在四边形 中, , ,且 ,则实数 的值为 , 若 是线段 上的动点,且 ,则 的最小值为 .
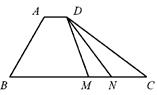 14. 已知x≥0,y≥0,且x+y=1,则x2+y2的取值范围是 .15. 已知抛物线C: , 点P为抛物线C上第一象限内任意一点,过点P向圆D:作切线,切点分别为A,B,则四边形PADB面积的最小值为 , 此时直线AB的方程为 .16. 已知函数和的表达式分别为 , , 若对任意 , 若存在 , 使得 , 则实数的取值范围是.17. 如图.在直角梯形中. , 点P是腰上的动点,则的最小值为 .
14. 已知x≥0,y≥0,且x+y=1,则x2+y2的取值范围是 .15. 已知抛物线C: , 点P为抛物线C上第一象限内任意一点,过点P向圆D:作切线,切点分别为A,B,则四边形PADB面积的最小值为 , 此时直线AB的方程为 .16. 已知函数和的表达式分别为 , , 若对任意 , 若存在 , 使得 , 则实数的取值范围是.17. 如图.在直角梯形中. , 点P是腰上的动点,则的最小值为 .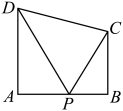 18. 已知正实数 , 称为的算术平均数,为的几何平均数,为的希罗平均数.为的边上异于的动点,点满足且 , 则正数的希罗平均数的最大值是 .19. 函数f(x)=x2-2(a-1)x+2在区间上是减函数,则实数a的范围是20. 已知平面向量、、、 , 满足 , , , , 若 , 则的最大值是.21. 如图.在平面四边形中, , ;若点为边上的动点,则的最小值为.
18. 已知正实数 , 称为的算术平均数,为的几何平均数,为的希罗平均数.为的边上异于的动点,点满足且 , 则正数的希罗平均数的最大值是 .19. 函数f(x)=x2-2(a-1)x+2在区间上是减函数,则实数a的范围是20. 已知平面向量、、、 , 满足 , , , , 若 , 则的最大值是.21. 如图.在平面四边形中, , ;若点为边上的动点,则的最小值为.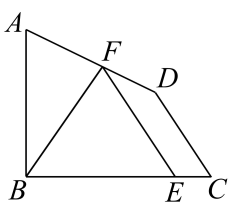 22. 在△ABC中, , , , , 则 , 若动点F在线段AC上,则的最小值为.23. 已知集合.给定一个函数 , 定义集合 , 若对任意的成立,则称该函数具有性质“”(1)、具有性质“”的一个一次函数的解析式可以是;(2)、给出下列函数:①;②;③ , 其中具有性质“”的函数的序号是.24. 已知正数满足 , 则的取值范围是.
22. 在△ABC中, , , , , 则 , 若动点F在线段AC上,则的最小值为.23. 已知集合.给定一个函数 , 定义集合 , 若对任意的成立,则称该函数具有性质“”(1)、具有性质“”的一个一次函数的解析式可以是;(2)、给出下列函数:①;②;③ , 其中具有性质“”的函数的序号是.24. 已知正数满足 , 则的取值范围是.三、解答题
-
25. 在直角坐标系 中,曲线C的参数方程为 (t为参数).以坐标原点为极点,x轴正半轴为极轴建立极坐标系,已知直线l的极坐标方程为 .(1)、写出l的直角坐标方程;(2)、若l与C有公共点,求m的取值范围.26. 已知函数.(1)、当时,求不等式的解集;(2)、若二次函数与函数的图象恒有公共点,求实数的取值范围.27. 在直角坐标系xOy中,曲线C的参数方程为(为参数),以坐标原点为极点,轴正半轴为极轴建立极坐标系,已知直线方程为(1)、写出的极坐标方程和曲线C的普通方程;(2)、点A为曲线C上一动点,点B为直线上一动点,求的最小值.28. 已知函数 .(1)、若复数(其中为虚数单位),求的值;(2)、过点的直线与切于点 , 求直线的斜率.29. 在中,角A,B,C的对边分别为a,b,c,且 , .(1)、若 , 求的周长;(2)、若内切圆、外接圆的半径分别为r,R,求的取值范围.30. 已知x,y为任意实数,有(1)、若求的最小值;(2)、求三个数中最大数的最小值.31. 已知椭圆 的右焦点为 ,长半轴长为 ,过焦点 且垂直于 轴的直线 交椭圆于 , .(1)、求椭圆 的方程;(2)、直线 是圆 的一条切线,且直线 与椭圆 相交于点 ,求 面积的最大值.32. 锐角 的内角A,B,C的对边分别为a,b,c,已知 .(1)、求A;(2)、若 ,D为AB的中点,求CD的取值范围.33. 已知a,b为正实数.(1)、证明:;(2)、若 , 证明: .34. 如图,正方体的棱长为2,E,F分别为和的中点,P为棱上的动点.
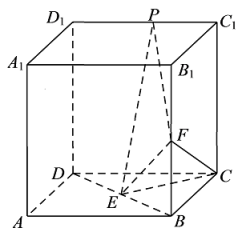 (1)、是否存在点P使平面?若存在,求出满足条件时的长度并证明;若不存在,请说明理由;(2)、当为何值时,平面与平面所成锐二面角的正弦值最小.35. 山西运城王过酥梨是国家农产品地理标志保护产品,王过酥梨含有多种对人体有益的钙、铁、磷等微量营养元素,食后清火润肺,止咳化痰,能起到祛病养生之效,一致被人们作为逢年过节走亲访友,馈赠待客及日常生活的必备佳品.某水果批发商小李从事酥梨批发多年,他把去年年底客户采购酥梨在内的数量x(单位:箱)绘制成下表:
(1)、是否存在点P使平面?若存在,求出满足条件时的长度并证明;若不存在,请说明理由;(2)、当为何值时,平面与平面所成锐二面角的正弦值最小.35. 山西运城王过酥梨是国家农产品地理标志保护产品,王过酥梨含有多种对人体有益的钙、铁、磷等微量营养元素,食后清火润肺,止咳化痰,能起到祛病养生之效,一致被人们作为逢年过节走亲访友,馈赠待客及日常生活的必备佳品.某水果批发商小李从事酥梨批发多年,他把去年年底客户采购酥梨在内的数量x(单位:箱)绘制成下表:采购数x(单位:箱)
客户数
5
10
15
15
5
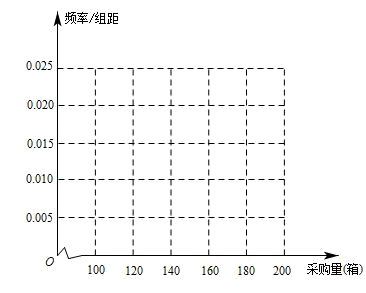 (1)、根据表中的数据,补充完整这些数据的频率分布直方图,并估计采购数在168箱以上(含168箱)的客户数;(2)、若去年年底采购在内的酥梨数量约占小李去年年底酥梨总销售量的 , 估算小李去年年底总销售量(同一组中的数据用该组区间的中点值作代表);(3)、在(2)的条件下,由于酥梨受到人们的青睐,小李做了一份市场调查以决定今年年底是否在网上出售酥梨,若没有在网上出售酥梨,则按去年的价格出售,每箱利润为14元,预计销售量与去年持平;若计划在网上出售酥梨,则需把每箱售价下调1至5元(网上、网下均下调),且每下调m元销售量可增加箱,试预计小李在今年年底销售酥梨总利润Y(单位:元)的最大值.
(1)、根据表中的数据,补充完整这些数据的频率分布直方图,并估计采购数在168箱以上(含168箱)的客户数;(2)、若去年年底采购在内的酥梨数量约占小李去年年底酥梨总销售量的 , 估算小李去年年底总销售量(同一组中的数据用该组区间的中点值作代表);(3)、在(2)的条件下,由于酥梨受到人们的青睐,小李做了一份市场调查以决定今年年底是否在网上出售酥梨,若没有在网上出售酥梨,则按去年的价格出售,每箱利润为14元,预计销售量与去年持平;若计划在网上出售酥梨,则需把每箱售价下调1至5元(网上、网下均下调),且每下调m元销售量可增加箱,试预计小李在今年年底销售酥梨总利润Y(单位:元)的最大值.