【备考2024】高考数学(函数版块)细点逐一突破训练:二次函数的图象
试卷更新日期:2023-08-17 类型:二轮复习
一、选择题
-
1. 已知函数 在区间(-∞,1]是减函数,则实数a的取值范围是()A、[1,+∞) B、(-∞,1] C、[-1,+∞) D、(-∞,-1]2. 设a≠0,若x=a为函数 的极大值点,则( )A、a<b B、a>b C、ab<a2 D、ab>a23. 已知曲线是平面内到定点和定直线的距离之和等于4的点的轨迹,若在曲线上,则下列结论正确的是( )A、曲线关于轴对称 B、曲线上任意一点到原点的距离都不超过 C、曲线及其内部共包含了19个整点(即横、纵坐标均为整数的点) D、点到点和点的距离之和最小为4. 设函数定义域为 , 为奇函数,为偶函数,当时, , 则下列结论错误的是( )A、 B、为奇函数 C、在上是减函数 D、方程仅有6个实数解5. 已知a、b是函数的两个零点,若 , , 则( )A、 B、 C、 D、6. 已知函数 , 其中为实数,则( )A、函数有两个不同零点0和; B、若对于任意两个不同的实数都有 , 则; C、若在[0,1]上单调递增,则或; D、若有三个不同的实数根,则.7. 已知 , ,c= , 则( )A、a<b<c B、b<a<c C、b<c<a D、c<a<b8. 已知函数 , ,当 时, 取得最大值b,则函数 的大致图象为( )A、
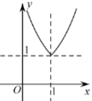 B、
B、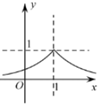 C、
C、 D、
D、 9. 定义 ,已知 为函数 的两个零点,若存在整数n满足 ,则 的值( )A、一定大于 B、一定小于 C、一定等于 D、一定小于
9. 定义 ,已知 为函数 的两个零点,若存在整数n满足 ,则 的值( )A、一定大于 B、一定小于 C、一定等于 D、一定小于二、填空题
-
10. 已知向量 , , 若 , 则点的轨迹方程为;若 , 则的最小值为.11. 设 表示函数 在闭区间 上的最大值.若正实数 满足 ,则 , 正实数 的取值范围是 .12. 罗默、伯努利家族、莱布尼兹等大数学家都先后研究过星形线 的性质,其形美观,常用于超轻材料的设计.曲线C围成的图形的面积S2(选填“>”、“<”或“=”),曲线C上的动点到原点的距离的取值范围是.13. 已知函数 ,若∃x1 , x2∈R,x1≠x2 , 使得f(x1)=f(x2)成立,则实数a的取值范围是 .14. 已知函数 ,则 , 若实数 ,且 ,则 的取值范围是 .15. 已知函数 ,函数 有三个零点,则实数 的取值范围为 .16. 若二次函数 的最小值为 ,则 的取值范围为 .
17. 已知点 , , 在二次函数 的图象上,且 ,则实数 的取值范围为.18. 若直线与函数的图像有两个不同交点,则实数m的取值范围是 .19. 函数 的定义域为 ,则实数 的取值范围为 .20. 函数 在区间 上不单调 , 则实数k的取值范围是 .三、解答题
-
21. 已知函数( , e为自然对数的底数).(1)、若函数有两个零点,求实数的取值范围;(2)、函数 , , 记的极小值为 , 求函数的值域.22. 已知函数 .(1)、当时,求不等式的解集;(2)、若二次函数与函数的图象恒有公共点,求实数m的取值范围.23. 已知函数f(x)=|x+a|(a∈R).(1)、若f(x)≥|2x﹣1|的解集为[0,2],求a的值;(2)、若对任意x∈R,不等式f(x)+|x﹣2a|≥a2﹣4a恒成立,求实数a的取值范围.24. 在① ,② ,③ 三个条件中任选一个,补充在下面问题中的横线上,并解决该问题.
问题:已知 的内角 及其对边 ,若 ,且满足___________.求 的面积的最大值(注:如果选择多个条件分别解答,按第一个解答计分)
25. 已知函数 .
(1)、当 时,若存在 ,使得 ,求实数 的取值范围;
(2)、若 为正整数,方程 的两个实数根 满足 ,求 的最小值.26. 已知函数 ,(1)、当时,求的单调递减区间;(2)、若有三个零点 , 且求证:①
②.
27. 已知函数 , .(1)、若在上有零点,求实数的取值范围;(2)、若在区间上的最小值为-2,求实数的值.28. 已知函数.(1)、如果函数为幂函数,试求实数a、b、c的值;(2)、如果、 , 且函数在区间上单调递减,试求ab的最大值.29. 已知函数.其中 , 且.(1)、求函数的单调区间;(2)、求函数在上的最小值.30. 已知.(1)、若f(x)在[0,2]上单调,求实数m的取值范围;(2)、若f(x)≤|mx-1|对x∈[0,4m]恒成立,求实数m的取值范围;(3)、若存在实数a,b,k满足f(a)=f(b)=k,且a<m<b.当m变化时,求a+b的取值范围.31. 已知函数 , , .(1)、若函数与的图象的一个交点的横坐标为2,求a;(2)、若 , 求证:.32. 已知函数.(1)、求曲线在点处的切线方程;(2)、当时,求的单调区间;(3)、求证:当≤时,≥.