【备考2024】高考数学(函数版块)细点逐一突破训练:函数的值2
试卷更新日期:2023-08-17 类型:二轮复习
一、选择题
-
1. 设f(x)= 若f(a)=f(a+1),则f( )=( )A、2 B、4 C、6 D、82. 函数y= 的部分图象大致为( )A、
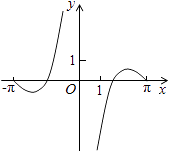 B、
B、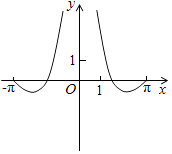 C、
C、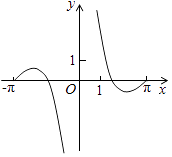 D、
D、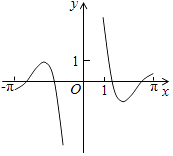 3. 已知定义在R上的函数 ,(e为自然对数的底数, ),则 ( )A、3 B、6 C、3e D、与实数m的取值有关4. 已知函数的定义域为 , 对任意 , 都有 . 现已知 , 那么( )A、 B、 C、 D、5. 已知 , 函数 , 若 , 则( )A、0 B、2 C、5 D、66. 若函数f(x)满足f(2x)=x,则f(5)=( )A、25 B、52 C、log52 D、log257. 已知是奇函数,当时, , 若 , 则( )A、 B、 C、2 D、18. 设函数的定义域为 , 为奇函数,为偶函数,当时,.若 , 则( )A、 B、 C、 D、9. 已知函数 , 则( )A、 B、 C、 D、10. 已知定义域为的函数的图象关于点成中心对称,且当时, , 若 , 则( )A、7 B、2 C、-2 D、11. 一热水放在常温环境下经过t分钟后的温度T将合公式: , 其中是环境温度,为热水的初始温度,h称为半衰期.一杯85℃的热水,放置在25℃的房间中,如果热水降温到55℃,需要10分钟,则一杯100℃的热水放置在25℃的房间中,欲降温到55℃,大约需要多少分钟?( )()A、11.3 B、13.2 C、15.6 D、17.112. 已知函数 , 则( )A、0 B、1 C、2 D、3
3. 已知定义在R上的函数 ,(e为自然对数的底数, ),则 ( )A、3 B、6 C、3e D、与实数m的取值有关4. 已知函数的定义域为 , 对任意 , 都有 . 现已知 , 那么( )A、 B、 C、 D、5. 已知 , 函数 , 若 , 则( )A、0 B、2 C、5 D、66. 若函数f(x)满足f(2x)=x,则f(5)=( )A、25 B、52 C、log52 D、log257. 已知是奇函数,当时, , 若 , 则( )A、 B、 C、2 D、18. 设函数的定义域为 , 为奇函数,为偶函数,当时,.若 , 则( )A、 B、 C、 D、9. 已知函数 , 则( )A、 B、 C、 D、10. 已知定义域为的函数的图象关于点成中心对称,且当时, , 若 , 则( )A、7 B、2 C、-2 D、11. 一热水放在常温环境下经过t分钟后的温度T将合公式: , 其中是环境温度,为热水的初始温度,h称为半衰期.一杯85℃的热水,放置在25℃的房间中,如果热水降温到55℃,需要10分钟,则一杯100℃的热水放置在25℃的房间中,欲降温到55℃,大约需要多少分钟?( )()A、11.3 B、13.2 C、15.6 D、17.112. 已知函数 , 则( )A、0 B、1 C、2 D、3二、填空题
-
13. 李明自主创业,在网上经营一家水果店,销售的水果中有草莓、京白梨、西瓜、桃,价格依次为60元/盒、65元/盒、80元/盒、90元/盒。为增加销量,李明对这四种水果进行促销:一次购买水果的总价达到120元,顾客就少付x元。每笔订单顾客网上支付成功后,李明会得到支付款的80%.
①当x=10时,顾客一次购买草莓和西瓜各1盒,需要支付元;
②在促销活动中,为保证李明每笔订单得到的金额均不低于促销前总价的七折,则x的最大值为。
14. 已知函数f(x)=log2(x2+a).若f(3)=1,则a=.
15. 设函数f(x)= ,则满足f(x)+f(x﹣ )>1的x的取值范围是 .16. 已知函数 , 则.17. 已知函数 , 对任意非零实数x,均满足.则的值为;函数的最小值为.18. 已知 , 则.19. 已知函数 ,若 ,则 .20. 已知函数 , 则 .21. 若 , 则.22. 若函数的反函数的图象经过点 , 则.23. 函数的反函数为 , 则.24. 若函数 ,则 .25. 定义在 上的函数 单调递增,且对 ,有 ,则 .三、解答题
-
26. 已知函数 的最小正周期为 ,且 .(1)、求 和 的值;(2)、若 ,求 .27. 若函数y=f(x)对定义域的每一个值x1 , 在其定义域均存在唯一的x2 , 满足f(x1)f(x2)=1,则称该函数为“依赖函数”.(1)、判断 ,y=2x是否为“依赖函数”;(2)、若函数y=a+sinx(a>1), 为依赖函数,求a的值,并给出证明.28. 设函数f(x)=|x+2|﹣|x﹣1|
(I)画出函数y=f(x)的图象;
(II)若关于x的不等式f(x)+4≥|1﹣2m|有解,求实数m的取值范围.
29. 已知函数(1)、求的值;(2)、若 , 且 , 再从下面①②③中选取一个作为条件,求的值.①函数的一个对称中心为;②函数图象过点;③两条相邻对称轴间的距离为 .30. 已知函数 , 其中.(1)、当时,若 , 求的值;(2)、记的最大值为 , 求的表达式并求出的最小值.31. 已知 , 且(1)、求的值;(2)、求在处的切线方程.32. 已知函数的图象在定义域上连续不断.若存在常数 , 使得对于任意的 , 恒成立,称函数满足性质.(1)、若满足性质 , 且 , 求的值;(2)、若 , 试说明至少存在两个不等的正数 , 同时使得函数满足性质和.(参考数据:)(3)、若函数满足性质 , 求证:函数存在零点.33. 已知函数的定义域为 , 且对 , , 都有 .(1)、求 , 并证明:;(2)、若当 , 有 , 给出两个论断:①当时,;②在上单调递增;请选择其中一个证明.