【备考2024】高考数学(函数版块)细点逐一突破训练:函数的值1
试卷更新日期:2023-08-17 类型:二轮复习
一、选择题
-
1. 函数 在区间 的图像大致为( )A、
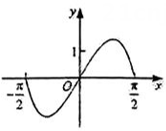 B、
B、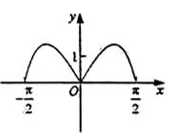 C、
C、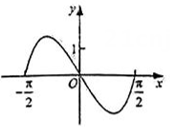 D、
D、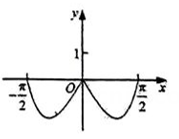 2. 已知函数 及其导函数 的定义域均为R,记 若 均为偶函数,则( )A、 B、 C、 D、3. 设函数f(x)的定义域为R , f(x+1)为奇函数,f(x+2)为偶函数,当 时, .若 ,则 ( )A、 B、 C、 D、4. 给出定义:设是函数的导函数,是函数的导函数.若方程有实数解 , 则称为函数的“拐点”.经研究发现所有的三次函数都有“拐点”,且该“拐点”也是函数的图象的对称中心.若函数 , 则( )A、-8080 B、-8090 C、-8092 D、-80965. 已知函数 , 则( )A、2 B、-2 C、 D、-6. 欧拉函数的函数值等于所有不超过正整数 , 且与互素(也称互质)的正整数的个数,例如 , , . 则( )A、数列单调 B、 C、数列是等比数列 D、7. 记函数的最小正周期为 . 若 , 且的图象的一条对称轴为 , 关于该函数有下列四个说法:
2. 已知函数 及其导函数 的定义域均为R,记 若 均为偶函数,则( )A、 B、 C、 D、3. 设函数f(x)的定义域为R , f(x+1)为奇函数,f(x+2)为偶函数,当 时, .若 ,则 ( )A、 B、 C、 D、4. 给出定义:设是函数的导函数,是函数的导函数.若方程有实数解 , 则称为函数的“拐点”.经研究发现所有的三次函数都有“拐点”,且该“拐点”也是函数的图象的对称中心.若函数 , 则( )A、-8080 B、-8090 C、-8092 D、-80965. 已知函数 , 则( )A、2 B、-2 C、 D、-6. 欧拉函数的函数值等于所有不超过正整数 , 且与互素(也称互质)的正整数的个数,例如 , , . 则( )A、数列单调 B、 C、数列是等比数列 D、7. 记函数的最小正周期为 . 若 , 且的图象的一条对称轴为 , 关于该函数有下列四个说法:①;
②;
③在上单调递增;
④为了得到的图象,只需将的图象向右平移个单位长度.
以上四个说法中,正确的个数为( )
A、1 B、2 C、3 D、48. 设函数的定义域为 , 且是奇函数,是偶函数,则一定有( )A、 B、 C、 D、9. 设函数 , 则( )A、5 B、6 C、7 D、810. 如图为函数的部分图象,则的值可能是( )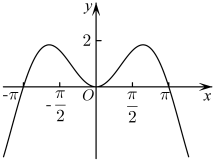 A、4 B、3 C、2 D、111. 若是奇函数,则( )A、 B、 C、 D、12. 已知函数 , 则( )A、 B、 C、 D、13. 函数满足 , , 函数的一个零点也是其本身的极值点,则可能的表达式有( )A、 B、 C、 D、
A、4 B、3 C、2 D、111. 若是奇函数,则( )A、 B、 C、 D、12. 已知函数 , 则( )A、 B、 C、 D、13. 函数满足 , , 函数的一个零点也是其本身的极值点,则可能的表达式有( )A、 B、 C、 D、二、填空题
-
14. 已知函数 , 则.15. 若函数 , 满足 , 且 , 则.16. 已知函数则 .17. 已知函数 , 则.18. 已知函数 , 则;若 , 且 , 则 .19. 若函数是偶函数,则 .20. 已知函数 , 若 , 则.21. 若函数 ,则 .22. 若函数 , 则 , 不等式的解集是 .23. 已知函数 , 则.
三、解答题
-
24. 已知函数 .(1)、若f(1)=2,求a的值;(2)、若存在两个不相等的正实数 ,满足 ,证明:
① ;
② .
25. 已知函数 .(1)、求 的值;(2)、求 的最小正周期.26. 某超市记录了某农副产品5个月内的月平均销售价格,得到的统计数据如下表:月份x
1
2
3
4
5
月平均销售价格(单位:元/千克)
12
10.5
10
8.5
9
参考公式:.
(1)、若月平均销售价格y与月份x之间的回归直线方程为 , 求的值;(2)、请根据(1)预测6月份该农副产品的月平均销售价格;(3)、求该农副产品5个月内的月平均销售价格这组数据的方差.27. 某医疗机构承担了某城镇的新冠疫苗接种任务.现统计了前8天每天(用 ,2,…,8表示)的接种人数 (单位:百)相关数据,并制作成如图所示的散点图:
参考数据: , , .参考公式:对于一组数据 , ,…, ,回归方程 中的斜率和截距的最小二乘估计公式分别为 , .
(1)、由散点图看出,可用线性回归模型拟合 与 的关系,求 关于 的回归方程(系数精确到0.01);(2)、根据该模型,求第10天接种人数的预报值;并预测哪一天的接种人数会首次突破2500人.28. 如图,在实验室细菌培养过程中,细菌生长主要经历调整期、指数期、稳定期和衰亡期四个时期.在一定条件下,培养基上细菌的最大承载量(达到稳定期时的细菌数量)与培养基质量具有线性相关关系.某实验室在培养细菌 的过程中,通过大量实验获得了以下统计数据:培养基质量x(克)
20
40
50
60
80
细菌A的最大承载量Y(单位)
300
400
500
600
700

参考数据: , , , .参考公式:回归方程 中斜率和截距的最小二乘估计公式分别为: , .
(1)、建立Y关于x的回归直线方程,并预测当培养基质量为100克时细菌A的最大承载量;(2)、研究发现,细菌 的调整期一般为3小时,其在指数期的细菌数量 (单位)与细菌 被植入培养基的时间 近似满足函数关系 ,试估计在100克培养基上培养细菌 时指数期的持续时间(精确到1小时).29. 物理学中常用“伏安法”测量电阻值(单位:欧姆),现用仪器测量某一定值电阻在不同电压下的电流值测得一组数据 ,其中, 和 分别表示第i次测量数据的电流(单位:安培)和电压(单位:伏特),计算得 .附:回归直线的斜率和截距的最小二乘估计公式分别为: .
(1)、用最小二乘法求出回归直线方程( 与 精确到0.01);(2)、由“伏安法”可知,直线的斜率是电阻的估计值,请用计算得到的数据说明电阻的估计值.30. 已知定义在R上的函数 满足 ,且当 时,(1)、求 的值;(2)、解不等式 ;(3)、若关于x的方程 在 上有解,求实数a的取值范围.31. 已知函数 的图象关于直线 对称,且图象上相邻两个对称中心的距离为 .(1)、求函数 的解析式;(2)、设 ,且 ,若 ,求 的值.32. 已知:①函数 ;②向量 , ,且 , ;
③函数 的图象经过点
请在上述三个条件中任选一个,补充在下面问题中,并解答.
已知_________________,且函数 的图象相邻两条对称轴之间的距离为 .
(1)、若 ,且 ,求 的值;(2)、求函数 在 上的单调递减区间.注:如果选择多个条件分别解答,按第一个解答计分.