【备考2024】高考数学(函数版块)细点逐一突破训练:函数的图象
试卷更新日期:2023-08-17 类型:二轮复习
一、选择题
-
1. 如图是下列四个函数中的某个函数在区间 的大致图像,则该函数是( )
 A、 B、 C、 D、2. 在北京冬奥会上,国家速滑馆“冰丝带”使用高效环保的二氧化碳跨临界直冷制冰技术,为实现绿色冬奥作出了贡献,如图描述了一定条件下二氧化碳所处的状态与 和 的关系,其中 表示温度,单位是 ; 表示压强,单位是bar,下列结论中正确的是( )
A、 B、 C、 D、2. 在北京冬奥会上,国家速滑馆“冰丝带”使用高效环保的二氧化碳跨临界直冷制冰技术,为实现绿色冬奥作出了贡献,如图描述了一定条件下二氧化碳所处的状态与 和 的关系,其中 表示温度,单位是 ; 表示压强,单位是bar,下列结论中正确的是( )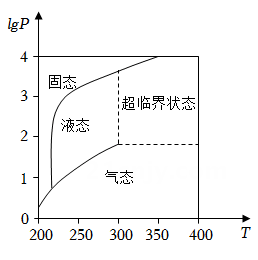 A、当 , 时,二氧化碳处于液态 B、当 , 时,二氧化碳处于气态 C、当 , 时,二氧化碳处于超临界状态 D、当 , 时,二氧化碳处于超临界状态3. 已知函数 若函数 恰有4个零点,则k的取值范围是( )A、 B、 C、 D、4. 已知函数 ,则不等式 的解集是( ).A、 B、 C、 D、5. 经济学家在研究供求关系时,一般用纵轴表示产品价格(自变量),而用横轴来表示产品数量(因变量).某类产品的市场供求关系在不受外界因素(如政府限制最高价格等)的影响下,市场会自发调解供求关系:当产品价格低于均衡价格时,需求量大于供应量,价格会上升为;当产品价格高于均衡价格时,供应量大于需求量,价格又会下降,价格如此波动下去,产品价格将会逐渐靠近均衡价格 . 能正确表示上述供求关系的图形是( ).A、
A、当 , 时,二氧化碳处于液态 B、当 , 时,二氧化碳处于气态 C、当 , 时,二氧化碳处于超临界状态 D、当 , 时,二氧化碳处于超临界状态3. 已知函数 若函数 恰有4个零点,则k的取值范围是( )A、 B、 C、 D、4. 已知函数 ,则不等式 的解集是( ).A、 B、 C、 D、5. 经济学家在研究供求关系时,一般用纵轴表示产品价格(自变量),而用横轴来表示产品数量(因变量).某类产品的市场供求关系在不受外界因素(如政府限制最高价格等)的影响下,市场会自发调解供求关系:当产品价格低于均衡价格时,需求量大于供应量,价格会上升为;当产品价格高于均衡价格时,供应量大于需求量,价格又会下降,价格如此波动下去,产品价格将会逐渐靠近均衡价格 . 能正确表示上述供求关系的图形是( ).A、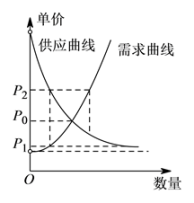 B、
B、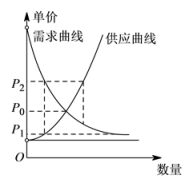 C、
C、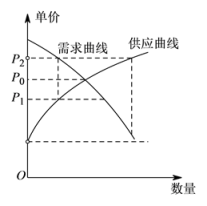 D、
D、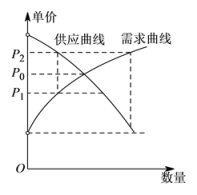 6. 已知函数 , 则的大致图象为( )A、
6. 已知函数 , 则的大致图象为( )A、 B、
B、 C、
C、 D、
D、 7. 函数的图象大致是( )A、
7. 函数的图象大致是( )A、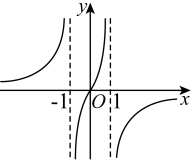 B、
B、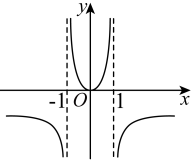 C、
C、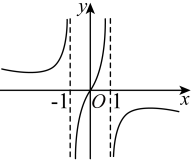 D、.
D、.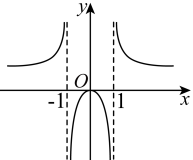 8. 如图,动点P从点M出发,按照路径运动,四边形ABCD是边长为2的正方形,弧DM以A为圆心,AD为半径,设点P的运动路程为x,的面积为y,则函数的图象大致是( )
8. 如图,动点P从点M出发,按照路径运动,四边形ABCD是边长为2的正方形,弧DM以A为圆心,AD为半径,设点P的运动路程为x,的面积为y,则函数的图象大致是( ) A、
A、 B、
B、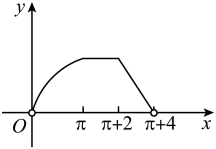 C、
C、 D、
D、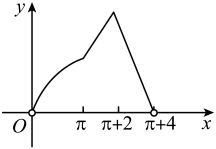 9. 函数的图象可能为( )A、
9. 函数的图象可能为( )A、 B、
B、 C、
C、 D、
D、 10. 已知函数 , 则的零点个数为( )A、2023 B、2025 C、2027 D、202911. 如图是下列某个函数在区间的大致图象,则该函数是( )
10. 已知函数 , 则的零点个数为( )A、2023 B、2025 C、2027 D、202911. 如图是下列某个函数在区间的大致图象,则该函数是( ) A、 B、 C、 D、12. 数学与音乐有着紧密的关联,我们平时听到的乐音一般来说并不是纯音,而是由多种波叠加而成的复合音.如图为某段乐音的图象,则该段乐音对应的函数解析式可以为( )
A、 B、 C、 D、12. 数学与音乐有着紧密的关联,我们平时听到的乐音一般来说并不是纯音,而是由多种波叠加而成的复合音.如图为某段乐音的图象,则该段乐音对应的函数解析式可以为( ) A、 B、 C、 D、13. 若函数与函数(且)的图像有且仅有一个交点,则的范围为( )A、 B、 C、 D、14. 函数的图象大致为( )A、
A、 B、 C、 D、13. 若函数与函数(且)的图像有且仅有一个交点,则的范围为( )A、 B、 C、 D、14. 函数的图象大致为( )A、 B、
B、 C、
C、 D、
D、
二、填空题
-
15. 已知集合 , ,存在正数 ,使得对任意 ,都有 ,则 的值是 .
16. 若函数的图象不过第四象限,则实数a的取值范围为 .17. 已知函数与的图象在区间上的交点个数为m,直线与的图象在区间上的交点的个数为n,则 .18. 若函数的图像上点与点、点与点分别关于原点对称,除此之外,不存在函数图象上的其它两点关于原点对称,则实数的取值范围是 .19. 据报道,我国目前已成为世界上受荒漠化危害最严重的国家之一.下左图表示我国土地沙化总面积在上个世纪五六十年代、七八十年代、九十年代的变化情况.由图中的相关信息,可将上述有关年代中,我国年平均土地沙化面积在下右图中图示为: .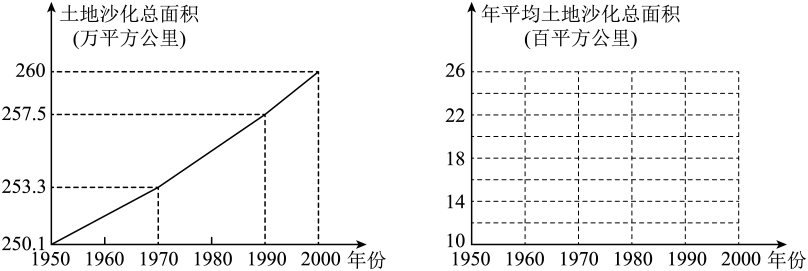 20. 已知 , 函数的最小值为 , 则的取值范围是:.21. 已知函数c若存在实数 , 使得关于的方程恰有三个不同的实数根,则的取值范围是 .22. 设函数 , , .则函数的图像与x轴所围成图形中的封闭部分的面积是.23. 若关于x的不等式有且只有2个正整数解,则实数a的取值范围为 .24. 已知 , 若函数有三个零点,则实数的取值范围是 .25. 函数在上有两个零点,则实数a的取值范围是.
20. 已知 , 函数的最小值为 , 则的取值范围是:.21. 已知函数c若存在实数 , 使得关于的方程恰有三个不同的实数根,则的取值范围是 .22. 设函数 , , .则函数的图像与x轴所围成图形中的封闭部分的面积是.23. 若关于x的不等式有且只有2个正整数解,则实数a的取值范围为 .24. 已知 , 若函数有三个零点,则实数的取值范围是 .25. 函数在上有两个零点,则实数a的取值范围是.三、解答题
-
26. 已知函数 .(1)、画出 的图像;
 (2)、求不等式 的解集.27. 已知函数 , .
(2)、求不等式 的解集.27. 已知函数 , . (1)、在给出的坐标系中画出函数的图像;(2)、若关于的不等式恒成立,求实数的取值范围.28. 设函数.(1)、求不等式的解集;(2)、求直线与的图象围成的三角形的面积的最大值.29. 已知函数.
(1)、在给出的坐标系中画出函数的图像;(2)、若关于的不等式恒成立,求实数的取值范围.28. 设函数.(1)、求不等式的解集;(2)、求直线与的图象围成的三角形的面积的最大值.29. 已知函数. (1)、画出的图象;(2)、若 , 求实数t的取值范围.30. 城市道路大多是纵横交错的矩形网格状,从甲地到乙地的最短路径往往不是直线距离,而是沿着网格走的直角距离,在直角坐标系中,定义点的“直角距离”为: , 设.
(1)、画出的图象;(2)、若 , 求实数t的取值范围.30. 城市道路大多是纵横交错的矩形网格状,从甲地到乙地的最短路径往往不是直线距离,而是沿着网格走的直角距离,在直角坐标系中,定义点的“直角距离”为: , 设. (1)、写出一个满足的点的坐标;(2)、过点作斜率为2的直线 , 点分别是直线上的动点,求的最小值;(3)、设 , 记方程的曲线为 , 类比椭圆研究曲线的性质(结论不要求证明),并在所给坐标系中画出该曲线;31. 已知函数f(x)=|x-1|,函数g(x)=m-|x|.(1)、当m=3时,求不等式f(x)≤g(x)的解集;(2)、若函数f(x)的图象恒在函数g(x)图象的上方,求实数m的取值范围.32. 已知函数f(x)=|x-1|,函数g(x)=m-|x|.(1)、当m=3时,求不等式f(x)≤g(x)的解集;(2)、若函数f(x)的图象恒在函数g(x)图象的上方,求实数m的取值范围.33. 已知函数 .
(1)、写出一个满足的点的坐标;(2)、过点作斜率为2的直线 , 点分别是直线上的动点,求的最小值;(3)、设 , 记方程的曲线为 , 类比椭圆研究曲线的性质(结论不要求证明),并在所给坐标系中画出该曲线;31. 已知函数f(x)=|x-1|,函数g(x)=m-|x|.(1)、当m=3时,求不等式f(x)≤g(x)的解集;(2)、若函数f(x)的图象恒在函数g(x)图象的上方,求实数m的取值范围.32. 已知函数f(x)=|x-1|,函数g(x)=m-|x|.(1)、当m=3时,求不等式f(x)≤g(x)的解集;(2)、若函数f(x)的图象恒在函数g(x)图象的上方,求实数m的取值范围.33. 已知函数 . (1)、在如图所示的网格中画出 的图象;(2)、若当 时、 恒成立,求 的取值范围.
(1)、在如图所示的网格中画出 的图象;(2)、若当 时、 恒成立,求 的取值范围.